
Астахов Основные разделы механики 2011
.pdf
сил (или равнодействующей силе):
|
p |
n |
|
lim |
= ∑Fi = Fр. |
(13.6) |
|
t→0 |
t |
i=1 |
|
Если равнодействующая сила постоянна (Fp = const) на промежутке времени t, то приращение импульса м.т. равно импульсу равнодействующей силы:
p = Fp t. |
(13.7) |
Импульс системы материальных точек равен сумме импуль-
сов всех м.т., принадлежащих данной системе:
n |
n |
|
pс = ∑pi = ∑mi vi , |
(13.8) |
|
i=1 |
i=1 |
|
где pi — импульс i-й м.т. массой mi, движущейся со скоростью vi.
Центр масс (центр инерции) системы м.т. rц.м — точка, ради-
ус-вектор которой определяется равенством:
n ∑miri
rц.м = i=1mc , (13.9)
где mi, ri — масса и радиус-вектор i-й м.т. соответственно, mс — масса системы материальных точек:
n |
|
mc = ∑mi . |
(13.10) |
i=1
Скорость центра масс системы материальных точек
|
|
n |
|
|
vц.м |
= |
∑mi vi |
(13.11) |
|
i=1 |
. |
|||
|
||||
|
|
mc |
|
|
Импульс системы м.т. может быть найден через произведение скорости центра масс и массы системы:
pс = mсvц.м. |
(13.12) |
41
Если система м.т. незамкнута, то скорость изменения импульса системы относительно ИСО равна равнодействующей всех внешних сил:
lim |
pс |
= F |
, |
(13.13) |
|
||||
t→0 |
t |
р внеш |
|
|
|
|
|
||
при этом |
|
|
|
|
|
|
n |
|
|
Fрвнеш = ∑Fрвнешi , |
(13.14) |
|||
i=1
где Fp.внеш i — равнодействующая внешних сил, действующих на i-ю материальную точку системы.
Если равнодействующая внешних сил постоянна (Fр.внеш = const) на промежутке времени t, то приращение импульса системы м.т. равно импульсу равнодействующей внешних сил:
pc = Fр.внеш t. |
(13.15) |
Равенству (13.15) эквивалентна система уравнений для проекций приращения импульса системы м.т. (при движении материальных точек в плоскости хОу):
|
p |
cx |
= F |
t, |
|
|
|
рвнеш x |
|
(13.16) |
|
|
pcy |
= Fрвнеш y |
t. |
||
|
|
||||
|
|
|
|
|
|
Закон сохранения импульса системы материальных точек
Относительно инерциальной системе отсчета (ИСО) импульс замкнутой системы материальных точек с течением времени не изменяется:
pз.с = const, |
(13.17) |
при этом взаимодействие между материальными точками системы может приводить к изменению их импульсов.
Равенству (13.17) эквивалентно равенство:
pз.с = 0. |
(13.18) |
42
Скорость центра масс замкнутой системы относительно ИСО с течением времени не изменяется:
vц.м..з.с = const. |
(13.19) |
Условие сохранения импульса незамкнутой системы материальных точек
Импульс незамкнутой системы м.т. pс с течением времени не изменяется, если сумма всех внешних сил, приложенных к материальным точкам системы, равна нулю:
pс = const при Fp.внеш = 0. |
(13.20) |
Равенству (13.20) эквивалентно равенство: |
|
pс = 0 при Fp.внеш = 0. |
(13.21) |
Условие сохранения проекции импульса незамкнутой системы материальных точек
Проекция импульса незамкнутой системы м.т. на какую-либо ось не изменяется, если проекция суммы всех внешних сил на эту ось равна нулю, например:
pс x = const при Fp.внеш x = 0. |
(13.22) |
Равенству (13.22) эквивалентно равенство: |
|
pс x = 0 при Fp.внеш x = 0. |
(13.23) |
Для решения некоторых задач можно считать, что |
|
pс = const, |
(13.24) |
если приращением импульса системы, по сравнению с начальным значением, можно пренебречь:
pс << pнс, |
(13.25) |
вследствие малых значений равнодействующей внешних сил и/или промежутка времени действия внешних тел, приводящих к малой величине импульса равнодействующей внешних сил.
43
§14. Работа и мощность
Работа постоянной силы при прямолинейном движении А — СФВ, равная скалярному произведению постоянной силы F на перемещение м.т. r, на котором действует эта сила:
|
|
|
|
A = (F, |
r) = F| r|cosα, |
(14.1) |
|
где сила F = const на |
r, α — угол между перемещением |
r и си- |
|||||
лой F (рис. 14.1). |
|
|
|
|
|
||
|
Единица работы — джоуль: [A] = Дж = кг м2/с2. |
|
|||||
|
F |
|
F |
|
|
Работа силы может быть поло- |
|
|
|
|
жительной, равной нулю и отрица- |
||||
|
m α |
m |
α |
|
|||
|
x |
тельной: |
|
||||
|
|
|
|
|
|||
0 |
l = |
r |
|
а) А > 0 при 0 ≤ α < π/2; |
|
||
Рис. 14.1 |
б) А = 0 при α = π/2; |
|
в) А < 0 при π/2 < α ≤ π. |
||
|
Работа постоянной силы может быть выражена также через
произведение: |
|
а) проекции силы на ось Ol, совпадающей по |
направлению с |
перемещением l, и модуля этого перемещения: |
|
A = Fl l, |
(14.2) |
б) проекции перемещения на ось OF, совпадающей по направ- |
|
лению с силой F, и модуля этой силы: |
|
A = lF F, |
(14.3) |
в) проекций силы и перемещения на координатные оси (при |
|
движении м.т. в плоскости хОу): |
|
A = Fх х + Fy y. |
(14.4) |
В частности, при прямолинейном движении материальной |
|
точки вдоль оси Ох работа постоянной силы |
|
A = Fx x. |
(14.5) |
Работа постоянной силы при прямолинейном движении вдоль
44
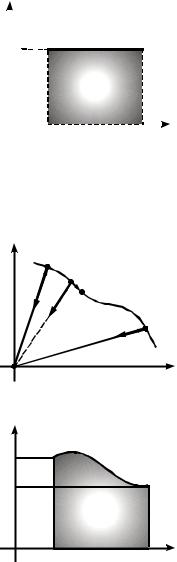
оси Ох в системе координат FxOx |
Fx |
|
|
|
|
|
|
|
равна площади (в единицах рабо- |
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
ты) прямоугольника, ограниченно- |
|
|
|
|
|
|
|
|
го графиком Fcx(х), осью Ох от на- |
Fcx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
чальной до конечной координаты |
|
|
|
|
|
|
|
|
м.т. и отрезками прямых х = хн и |
|
|
|
|
|
|
A |
|
х = хк (рис. 14.2). |
|
|
|
|
|
|
||
Работа переменной силы при |
|
|
|
|
|
|
|
|
произвольном движении матери- |
|
|
|
|
|
|
|
|
|
О |
|
|
|
xн |
xк x |
||
альной точки — СФВ, равная пре- |
|
|
|
|
|
|
Рис. 14.2 |
|
делу суммы скалярных произведе- |
|
|
|
|
|
|
||
ний силы Fi (рис. 14.3) на переме-
щение м.т. ri, на котором действует эта сила, при бесконечном уменьшении перемещений ri:
n
A = lim ∑Fi ri . (14.6)
ri →0 i=1
Работа переменной силы при прямолинейном движении м.т. вдоль оси Ох
n
A = lim ∑Fix xi . (14.7)
xi →0 i=1
Работа такой силы в системе координат FxOx равна площади (в единицах работы) криволинейной трапеции (рис. 14.4), ограниченной графиком Fx(х), осью Ох и отрезками прямых х = хн и х = хк.
Средняя мощность <Р> —
СФВ, равная отношению работы к промежутку времени t, за который совершена эта работа:
Р = |
A |
. |
(14.8) |
|
|||
|
t |
|
|
y |
|
|
|
|
|
|
rн |
|
ri |
|
|
|
Fн |
|
|
|
|
|
|
|
|
|
|
|
|
Fi |
Fк |
rк |
|
|
|
|
|
||
О |
|
Рис. 14.3 |
|
x |
|
|
|
|
|
||
Fx |
|
|
|
|
|
Fнx |
|
|
|
|
|
Fкx |
|
|
|
|
|
|
|
|
A |
|
|
О |
|
xн |
|
xк |
x |
|
|
Рис. 14.4 |
|
|
|
45
Мощность (мгновенная) Р — СФВ, равная пределу отношения элементарной работы δA к промежутку времени t, за который совершена эта работа, при бесконечном уменьшении промежутка времени:
P = lim |
δA . |
(14.9) |
t→0 |
t |
|
Единица мощности — ватт: [Р] = Вт = кг м2/с3.
Мощность P может быть выражена через скорость v и силу F, приложенную к материальной точке. Она равна их скалярному произведению:
P = (F,v) = Fvcosα , |
(14.10) |
где α — угол между силой F и скоростью v материальной точки. Мощность также может быть выражена через Fv — проекцию
силы на ось Ov, совпадающую по направлению со скоростью v, или через vF — проекцию скорости на ось OF, совпадающую по направлению с силой F:
P = Fvv = FvF , |
(14.11) |
либо через проекции силы и скорости на координатные оси (при движении м.т. в плоскости хОу):
P = Fхvх + Fуvу. |
(14.12) |
Работа упругой силы может быть определена из следующих равенств:
А |
|
= |
1 |
F |
|
|
x |
|
− |
1 |
|
F |
|
|
х |
|
, |
(14.13) |
||||
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||
|
упр |
|
|
упр.к x |
|
|
к |
|
|
упр.н х |
|
н |
|
|
||||||||
|
|
Аупр = |
1 |
кxн2 |
− |
1 |
|
кхк2 , |
|
|
|
|
(14.14) |
|||||||||
|
|
2 |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Аупр = |
|
1 Fупр2 |
.н |
− |
1 |
|
Fупр2 |
.к |
, |
|
|
(14.15) |
|||||||||
|
|
2 |
|
|
к |
|
|
2 |
|
к |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где хн и xк — начальное и конечное смещения незакрепленного конца пружины, к которому приложена внешняя сила Fвнеш (рис. 14.5а), к — жесткость пружины.
46
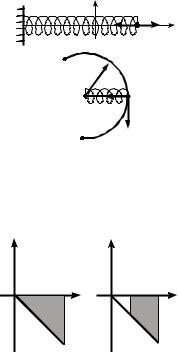
Работа упругой силы может быть положительной, отрицатель- |
|||||
ной и равной нулю: |
|
|
|
|
|
а) Aупр > 0 — при уменьшении удлинения (укорочения) пру- |
|||||
жины; |
|
y |
Fупр |
|
|
б) Aупр < 0 — при увеличении |
а) |
Fвнеш |
|||
длины пружины при растяжении |
0 |
|
x |
||
или уменьшении длины при сжатии |
|
|
|||
|
R |
|
|||
пружины; |
|
A |
|
||
в) Aупр = 0 — при угле между |
|
Fупр |
|
||
|
|
|
|||
силой упругости и скоростью м.т., |
б) |
|
|
||
равном 90° (например, при движе- |
|
B |
|
|
|
нии м.т. по дуге АВ окружности, |
|
v |
|
||
представленной на рис. 14.5, б), или |
|
|
|
|
|
при замкнутой траектории. |
|
Рис. 14.5 |
|
||
Работа упругой силы в системе |
|
|
|
|
|
координат Fупр.хOx равна площади (в единицах работы) прямо- |
|||||
угольного треугольника при растяжении или сжатии пружины (на |
|||||
рис. 14.6,а – при растяжении) из не- |
|
Fупр x |
Fупр x |
|
|
нагруженного (хн = 0) состояния или |
|
|
|||
площади трапеции при растяжении |
|
|
|
|
|
или сжатии пружины из нагружен- |
|
xк |
xн |
xк |
|
ного (хн ≠ 0) состояния (на рис.14.6,б |
О |
||||
x |
О |
x |
|||
– при растяжении), ограниченных |
|
|
|
|
|
соответствующим графиком Fупр.x(х), |
|
|
|
|
|
осью Ох от начальной до конечной |
|
|
|
|
|
координаты незакрепленного конца |
|
a) |
б) |
|
|
пружины и отрезками прямых х = хн |
|
Рис. 14.6 |
|
||
(в первом случае хн = 0) и х = хк. |
|
|
|||
Работа упругой силы определяется только начальным и конеч- |
|||||
ным положениями м.т. и не зависит от траектории между этими |
|||||
точками. |
|
|
|
|
|
Работа силы тяжести |
|
|
|
|
|
Aтяж = mg(hн – hк) |
(14.19) |
где hн и hк — начальная и конечная высоты (рис. 14.7) материальной точки массой m, g — модуль ускорения свободного падения.
47

|
Работа силы тяжести Aтяж определяется начальным и конеч- |
||||
y |
|
|
ным |
положениями |
материальной |
|
|
точки и не зависит от траектории |
|||
|
|
|
|||
hн |
|
|
между ними. |
|
|
|
|
|
|
Она может быть положитель- |
|
h к |
|
|
ной, отрицательной и равной нулю: |
||
mg |
|
|
а) Aтяж > 0 — при спуске мате- |
||
|
|
|
риальной точки, |
|
|
О |
xк |
xн x |
|
б) Aтяж < 0 — при подъеме ма- |
|
териальной точки, |
|
||||
|
Рис. 14.7 |
|
|
||
|
|
|
в) Aтяж = 0 — при условии, что |
||
высота не изменяется, либо при замкнутой траектории материаль- |
|||||
ной точки. |
|
|
|
|
|
|
Работа силы трения при постоянных скорости м.т. (v = const ) |
||||
и силы трения (Fтр = const) на промежутке времени |
t: |
||||
|
Aтр = (Fтр,v) t, |
|
|
(14.20) |
|
Работа силы трения может быть положительной, отрицатель- |
|||||
ной и равной нулю. Например: |
|
|
|
|
|
а) работа силы трения, действующей на нижний брусок со сто- |
|||||
y |
|
роны верхнего бруска (рис. 14.8), |
|||
v1 |
Aтр.2,1 > 0, т.к. угол между силой, |
||||
|
действующей на нижний брусок со |
||||
Fтр1,2 |
Fвнеш |
стороны верхнего бруска Fтр.2,1 и |
|||
|
1 |
скоростью v2 нижнего бруска (отно- |
|||
|
Fтр 2,1 |
сительно поверхности Земли) равен |
|||
|
нулю; |
|
|
|
|
2 |
|
|
|
|
|
x |
б) Aтр.1,2 < 0 — угол между си- |
||||
О |
лой трения |
Fтр.1,2 и |
скоростью v1 |
||
|
v2 |
верхнего |
бруска |
равен |
180° |
|
Рис. 14.8 |
||||
|
(см. рис. 14.8); |
|
|
||
|
|
в) Атр = 0 — например, брусок |
|||
находится на вращающемся горизонтальном диске (относительно |
|||||
диска брусок неподвижен). |
|
|
|
|
|
Работа силы трения зависит от траектории между начальным и |
|||||
конечным положениями материальной точки. |
|
|
|||
48
§15. Механическая энергия
Кинетическая энергия материальной точки K — СФВ, равная половине произведения массы м.т. на квадрат модуля ее скорости:
K = |
mv2 |
. |
(15.1) |
|
2 |
||||
|
|
|
Кинетическая энергия, обусловленная движением тела, зависит от системы отсчета и является неотрицательной величиной:
K≥ 0. |
(15.2) |
Единица кинетической энергии — джоуль: [К] = Дж.
Теорема о кинетической энергии — приращение кинетической энергии м.т. равно работе Aр равнодействующей силы:
K = Aр. |
(15.3) |
Работа равнодействующей силы может быть найдена как сумма работ Аi всех сил Fi (i = 1,2,…n), приложенных к м.т.:
n |
|
Ар = ∑Аi . |
(15.4) |
i=1
Модуль скорости материальной точки: при Aр > 0 — увеличивается; при Aр < 0 — уменьшается; при Aр = 0 — не изменяется.
Кинетическая энергия системы материальных точек Kс рав-
на сумме кинетических энергий Ki всех n м.т., принадлежащих данной системе:
n |
n |
2 |
|
|
|
Кс = ∑Кi = ∑ |
mi vi |
, |
(15.5) |
||
2 |
|||||
i=1 |
i=1 |
|
|
||
где mi и vi — масса и модуль скорости i-й м.т. данной системы.
Приращение кинетической энергии системы м.т. Kс равно сумме работ Арi всех n равнодействующих сил, приложенных к i-м материальным точкам системы:
n |
|
Кс = ∑Арi . |
(15.6) |
i=1
49
Поле сил — область пространства, в каждой точке которой на тело действуют силы.
Стационарное поле сил — поле, силы которого не изменяются с течением времени.
Однородное поле сил — поле, силы которого во всех его точках одинаковы.
Центральное поле сил — поле, направления действия всех сил которого проходят через одну точку, называемую центром поля, а модуль сил зависит только от расстояния до этого центра.
Неконсервативные силы (нк.сл) — силы, работа которых зави-
сит от траектории между начальным и конечным положениями тела.
Пример неконсервативных сил — силы трения. Работа сил трения по замкнутой траектории в общем случае не равна нулю.
Консервативные силы (к.сл) — силы, работа которых определяется начальным и конечным положениями м.т. и не зависит от траектории между ними. При замкнутой траектории работа консервативных сил равна нулю. Поле консервативных сил называется потенциальным.
Пример консервативных сил — силы тяжести и упругости. Потенциальная энергия П — СФВ, являющаяся функцией вза-
имного расположения частей системы (тела).
Единица потенциальной энергии — джоуль: [П] = Дж. Теорема о потенциальной энергии — убыль потенциальной
энергии системы материальных точек равна работе консервативных сил:
– П = Пн – Пк = Aк.сл |
(15.7) |
Потенциальная энергия определяется с точностью до постоянной величины и может быть положительной, отрицательной или равной нулю.
Потенциальная энергия материальной точки в какой-либо точке потенциального поля может быть определена через работу консервативных сил при перемещении м.т. из данной точки поля в точку, потенциальная энергия в которой принята равной нулю:
П = Aк.сл. |
(15.8) |
50
