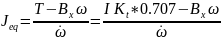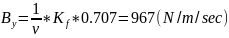2.2. Реализация обратной связи по положению
Используется управляющий элемент – контроллер − Turbo PMAC2, который замыкает контур сервопривода положения в цифровом виде для каждого управляемого двигателя. Цель контура сервопривода по положению состоит в том, чтобы попытаться привести фактическое положение двигателя в соответствие с заданным положением в каждый момент времени. Подробная структурная схема обратной связи по положению показана на рис. 14. Контроллер (Turbo PMAC2) разработан таким образом, чтобы позволять использовать ПИД-регуляторы. Они просты в понимании и настройке, но в то же время достаточно мощны, чтобы обеспечить хороший контроль над многими системами. Обратной связью контура сервопривода положения является сигнал положения от датчиков.
Рисунок 14
2.3. Реализация обратной связи по току
Подробная структурная схема части обратной связи по току, которая включает в себя некоторые части управляющего элемента, усилителя и двигателя, показана на рис. 15. Ток, генерируемый контуром сервопривода положения, сравнивается с фактическим током, измеряемым катушкой двигателя. Внутри контура тока для цифрового вычисления используется предварительно масштабированная квадратурная форма тока. Следовательно, для обратной связи аналого-цифровой преобразователь (АЦП) и преобразование из трехфазной формы (abc) в прямую/квадратурную (dq) форму тока. Выходные команды представлены в формате цифрового ШИМ-сигнала, и этот сигнал активирует двигатель через усилитель.
Рисунок 15
2.4. Структурная схема и математическое описание электромеханической части привода подачи
Вязкий
сдвиг, присутствующий в направляющих,
является единственным компонентом
коэффициента вязкого трения (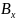
,
)
в системе электромеханического привода
подачи по оси y и х. Эквивалентный момент
инерции
относится к общей инерции, которую
должен преодолеть серводвигатель при
ускорении оси x. Это значение состоит
из двух составляющих. Первая — это
инерция сервомотора, муфты и винта,
которые вращаются с одинаковой скоростью.
И вторая – это отраженная инерция
линейных движущихся частей (например,
стола, гайки и т.д.). Для оси y – масса M
представляет общую движущуюся массу
вдоль оси y. Колонна, шпиндель и ротор
линейного двигателя входят в комплект
поставки. Эти четыре системных параметра,
,
,
и M находятся с помощью эксперимента и
вычислений.
Подробные структурные схемы электромеханических систем по осям х и у представлены на рис. 16 и рис. 17 соответственно
Рисунок 16
Рисунок 17
Из-за сложности моделирования вязкого сдвига между гидростатическими винтами и гайками внутри, комбинированное вязкое трение измеряется непосредственно на приводе подачи по оси x. Достигается это путем управления скоростью подачи с постоянной скоростью по оси x и записи выходного тока серводвигателя. Как видно из рис.16, крутящий момент двигателя может быть выражен как:
|
(4) |
Как
только привод подачи достигает постоянной
заданной скорости, ускорение
в уравнении (4) равно нулю. Это приводит
к зависимости, показанной в уравнении
(5), между угловой скорость подачи ω и
крутящим моментом двигателя T:
|
(5) |
Умножение
среднеквадратичного (среднеквадратичного)
тока на постоянный крутящий момент
серводвигателя (
)
приводит к мгновенному крутящему моменту
двигателя. Следовательно, окончательное
уравнение для
может быть сформулировано, как показано
в уравнении (6):
|
(6) |
Ток от катушки серводвигателя измеряется при различных скоростях подачи. Пример данных о токе и скорости подачи приведен на рис. 18, на котором представлены измерения, выполненные при постоянной скорости подачи 50.27 рад/сек. Получены средние значения скорости подачи и тока при постоянной заданной скорости. По результатам этих измерений ток двигателя отображается в зависимости от скорости подачи, как показано на рис. 19, где фактические данные представлены точками, а сплошная линия представляет собой линейную регрессию, соответствующую полученным данным. Основываясь на данном измерении и используя уравнение (6), коэффициент вязкого трения по оси x получается следующим образом.
|
(7) |
Рисунок 18
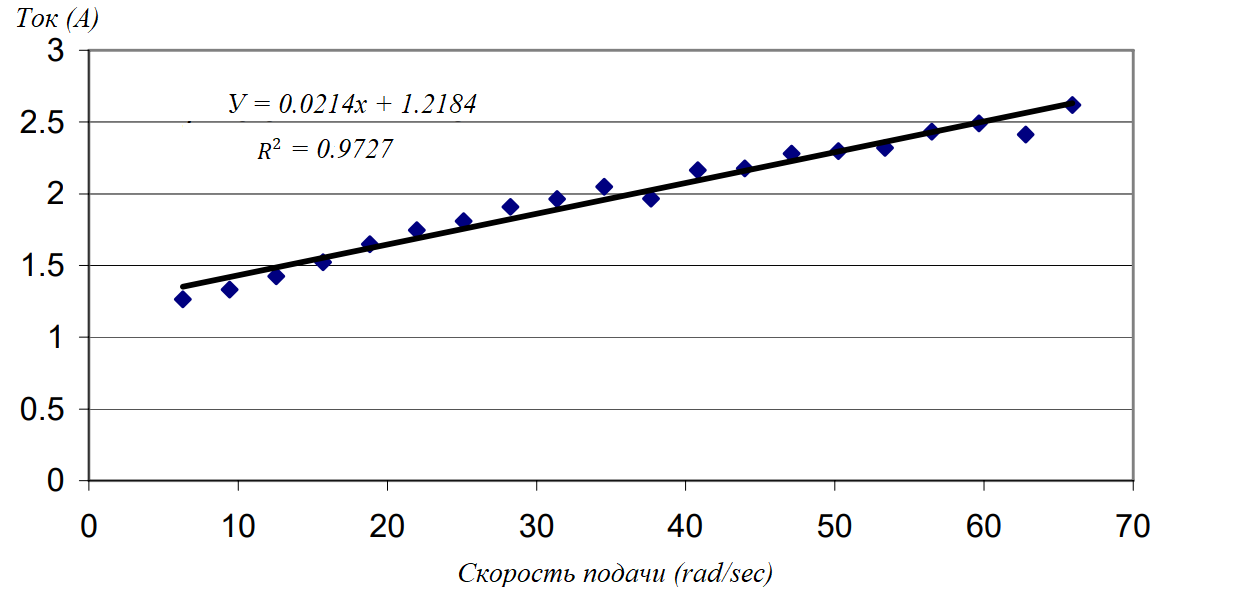
Рисунок 19
Эквивалентный момент инерции может быть оценен путем измерения характеристик всех параметров, которые вносят вклад в момент инерции в системе привода подачи по оси x. Но из-за сложности измерения точных характеристик всех составляющих эквивалентный момент инерции на приводе подачи по оси x также получается экспериментально. Уравнение (4) можно переставить в следующем виде:
|
(8) |
Рисунок 20
Данные о токе и скорости подачи представлены на рис. 20 для измерений, выполненных при постоянном ускорении 188,5 rad/sec2. Средние значения тока и скорости подачи получаются при постоянном ускорении. Исходя из этих измерений, эквивалентный момент инерции может быть рассчитан с использованием уравнения (8). В таблице 1 приведены сводные данные, полученные для в ходе нескольких экспериментов с использованием различных скоростей подачи и ускорений.
Таблица – 1.
Скорость подачи (рад/сек) |
Ускорение (рад/сек2) |
Ток (А) |
Момент инерции (Кгм2) |
50.3 |
189 |
15.2 |
0.0628 |
314 |
24.2 |
0.0608 |
|
503 |
36.7 |
0.0583 |
|
628 |
45.2 |
0.0575 |
|
62.8 |
189 |
15.2 |
0.0628 |
314 |
24.2 |
0.0602 |
|
503 |
36.7 |
0.0586 |
|
628 |
45.2 |
0.0578 |
|
69.1 |
189 |
15.2 |
0.0611 |
314 |
24.2 |
0.0583 |
|
503 |
36.7 |
0.0569 |
|
628 |
45.2 |
0.0576 |
|
81.7 |
189 |
15.2 |
0.0612 |
314 |
24.2 |
0.0586 |
|
503 |
36.7 |
0.0567 |
|
628 |
45.2 |
0.0574 |
|
Среднее |
|
|
0.0591 |
На
рис. 21 сравниваются позиции на фрезерном
станке
с позицией модели Simulink model
.
Рисунок 21 (б) представляет собой
увеличенный вид, показывающий начало
движения. Изучив реакцию реального
фрезерного станка и модели, можно
увидеть, что они очень хорошо согласуются,
однако при этом запаздывают относительно
заданной команды. Основываясь на этом
сравнении, точность модели считается
достаточной для того, чтобы приступить
к моделированию управляющих элементов.
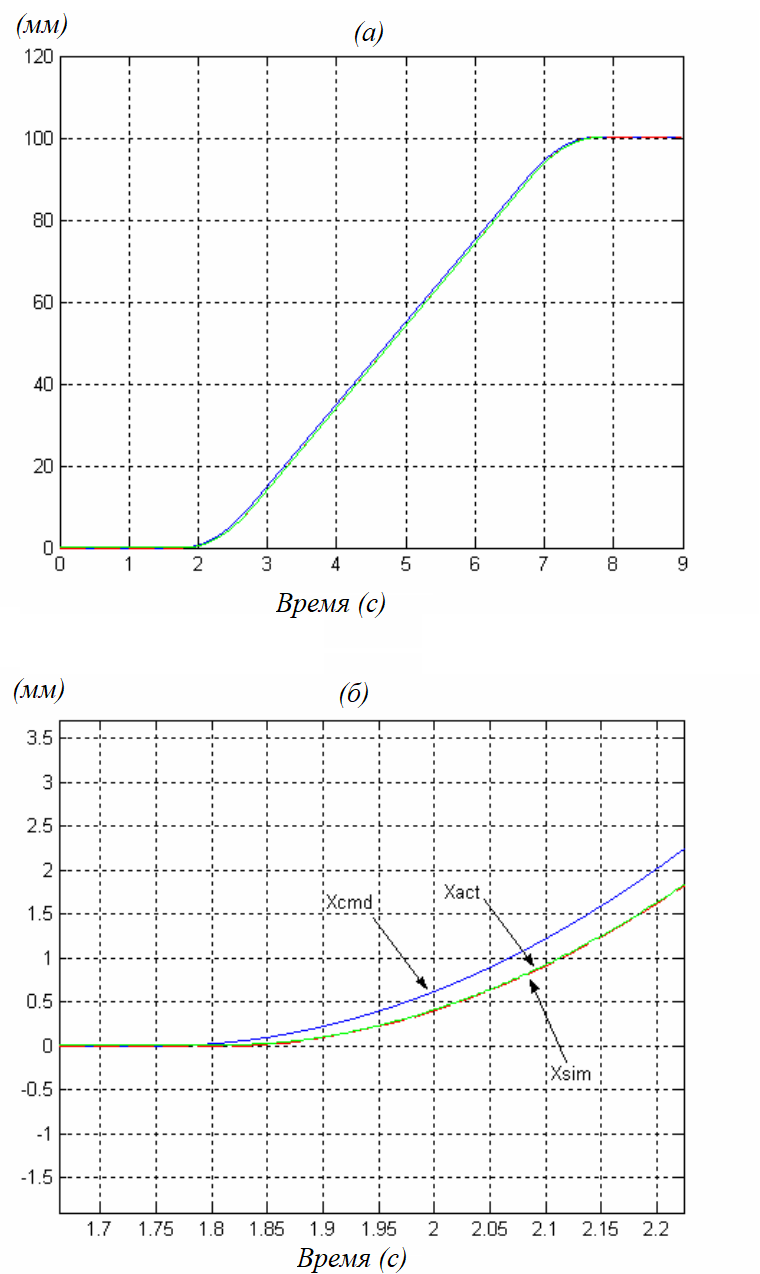
Рисунок 21
Аналогичная последовательность, которая использовалась для моделирования вязкого трения по оси x, применяется и к оси y. На рис. 17 сила может быть выражена так, как показано в уравнении (9):
|
(9) |
Как
только привод подачи достигает постоянной
скорости,
.
Это приводит к следующей зависимости,
показанной в уравнении (10), между скоростью
подачи
и усилием двигателя
:
|
(10) |
Умножение
среднеквадратичного тока на постоянную
силы серводвигателя (
)
приводит к мгновенному усилию двигателя.
Следовательно, окончательное уравнение
для
может быть сформулировано, как показано
в уравнении (11):
|
(11) |
Ток от катушки серводвигателя измеряется при различных скоростях подачи. Данные о токе и скорости подачи приведены на риc. 22 для измерения, выполненного при постоянной скорости подачи 0,1 м/с. Из текущих графиков на рис. 22 видно, что два линейных двигателя ведут себя совершенно одинаково. Следовательно, средние значения скорости подачи и тока могут быть получены на любом из двух графиков. По результатам этих измерений ток двигателя отображается в зависимости от скорости подачи, как показано на рис. 23, где фактические данные представлены точками, а сплошная линия представляет собой линейную регрессию, соответствующую полученным данным. Основываясь на этом измерении и используя уравнение (11), значение вязкого трения получается следующим образом:
|
(12) |
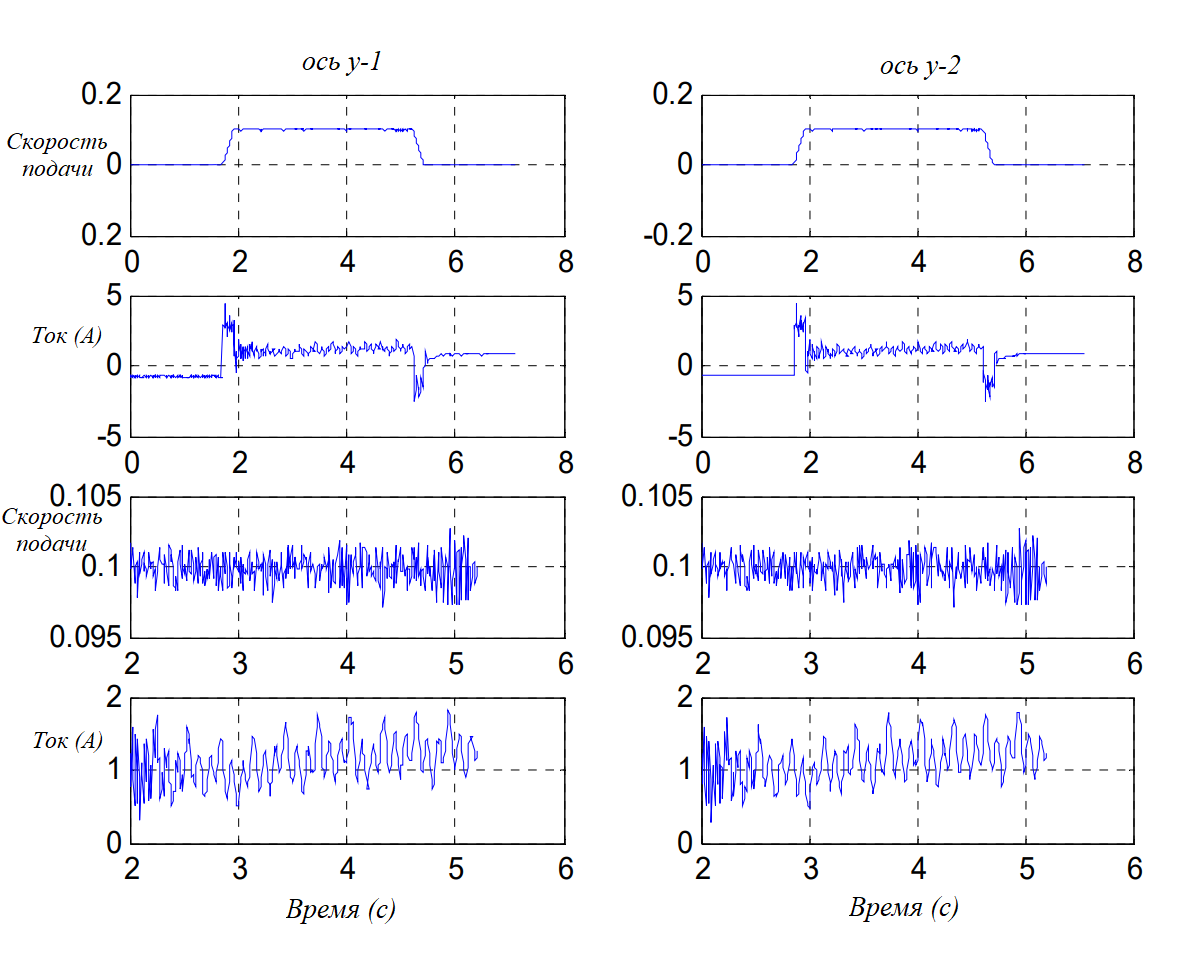
Рисунок 22
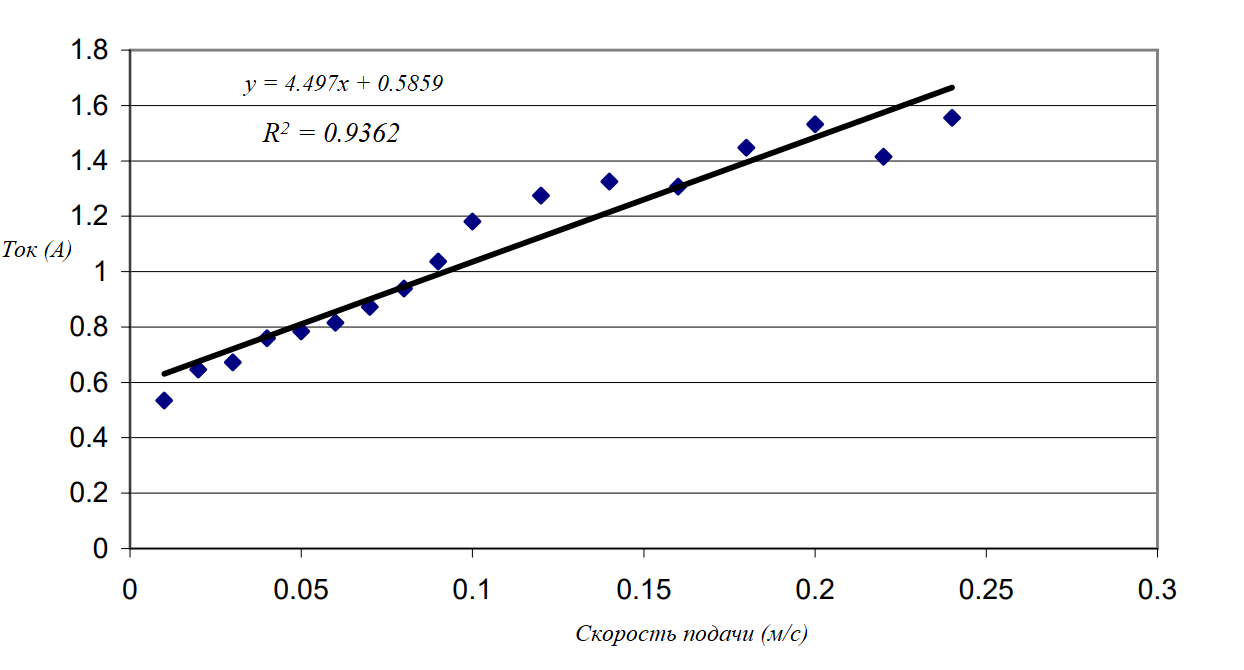
Рисунок 23
Та же последовательность, которая использовалась для определения момента инерции оси x, применяется и для оси y при моделировании общей движущейся массы. Уравнение (9) может быть представлено в следующем виде:
|
(13) |
Данные о токе и скорости подачи представлены на рис. 46 для измерений, выполненных при постоянном ускорении 800 мм/сек2. Среднее значение тока и скорости подачи получается в течение периода при постоянном ускорении. Исходя из этого измерения, общая движущаяся масса может быть рассчитана с использованием уравнения (13). В таблице 2 приведена сводная информация о полученных значениях для M в ходе нескольких экспериментов с использованием различных скоростей подачи и ускорений.
Рисунок 24
Таблица – 2.
Скорость подачи (м/сек) |
Ускорение (м/сек2) |
Масса (кг) |
0.15 |
0.5 |
1153 |
0.8 |
1196 |
|
1.0 |
1146 |
|
0.2 |
0.5 |
1153 |
0.8 |
1196 |
|
1.0 |
1146 |
|
0.26 |
0.8 |
1153 |
1.0 |
1196 |
|
1.5 |
1146 |
|
0.32 |
0.8 |
1153 |
1.0 |
1196 |
|
1.5 |
1146 |
|
Среднее |
|
1144 |
Используя Turbo PMAC2, приводу оси y подается команда на увеличение скорости при замкнутых контурах обратной связи по току и положению. Требуемая скорость подачи составляет 40 мм/с.
Во время перемещений заданное положение, рассчитанное с помощью ЧПУ, и фактическое положение, выбранное с помощью кодера, записываются в файл данных для последующего сравнения с моделью привода подачи в MATLAB Simulink.
На
рис. 25 представлено сравнение контурной
позиции фактической
на фрезерном станке с позицией
на модели MATLAB Simulink. Рис. 25(б) представляет
собой увеличенный вид, показывающий
начало движения. Изучив реакцию фрезерного
станка и модели, можно увидеть, что они
очень хорошо согласуются, однако отстают
от заданного. Основываясь на этом
сравнении, точность модели считается
достаточно высокой, чтобы приступить
к моделированию управляющих элементов.
Рисунок 25