3.2.1. Определение и квантование длин перемещения

В следующей части инициализации скорости подачи должны быть достигнуты в конце каждого этапа и расстояния , которые необходимо преодолеть на каждом этапе, рассчитываются из уравнения (40) и (42).

Количество шагов интерполяции для каждой фазы вычисляется следующим образом:

(61)

если какие-либо из 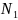, , или равны нулю для соответствующих ненулевых , , 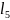и , они принимаются равными единице. Затем общее количество шагов для этапов ускорения и замедления вычисляется как,

(62)

и количество шагов для ступеней ускорения и замедления без рывков получается как,

(63)

которые дают количество шагов постоянной скорости подачи как

(64)

Используя приращение пути и количество шагов интерполяции для каждого этап, длины перемещения квантуются как,

(65)

3.2.2. Корректировка значений ускорения и рывка

После квантования длины хода значения ускорения, времени и рывка корректируются для получения заданных скоростей подачи для новых длин хода.

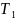Для этапа ускорения выражения , и в уравнении (43) используются для корректировки значений , и , что также приведет к корректировке из-за уравнения (43).

Для случая выражение для подставляется из уравнения (45) и , и заменяются на 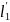', и соответственно, что приводит к следующим уравнениям, которые необходимо решить для , и ,

(66)

3.3. Математическое описание динамики фрезерного станка

Предполагается, что динамическая модель для трехосного станка с ЧПУ имеет следующий вид

(67)

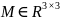где обозначают положение, скорость и ускорение станка соответственно, выраженные в инерциальной системе координат, обозначает неизвестную диагональную матрицу инерции, обозначает неизвестную диагональну матрицу трения, а  представляет входную управляющую силу. Чтобы облегчить последующую разработку КПС, координаты станка могут быть преобразованы из инерциальной системы координат в изменяющуюся во времени систему координат следующим образом

(68)

где обозначают положение, скорость и ускорение станка соответственно, выраженные в изменяющейся во времени системе координат.

Последующая разработка основана на предположении, что поддаются измерению. В уравнении (68), известная матрица преобразования состоит из единичногокасательного вектора, обозначаеммого , из единичного вектора нормали, обозначаемого , и единичного бинормального вектора, обозначаемого , определяемого как . Векторы определяются на основе касательной и нормальной составляющих желаемого контура, обозначаемых . То есть, учитывая желаемый контур , тангенциальную, нормальную и бинормальную составляющие можно использовать для изменения координат станка с инерциальной системы отсчета на изменяющуюся во времени систему отсчета следующим образом

(69)

где обозначают желаемое положение, скорость и ускорение станка, выраженные в изменяющейся во времени системе координат соответственно (рис. 48)

Рисунок 48

Основываясь на уравнениях (68) и (69), динамическая модель, приведенная в уравнении (67), может быть преобразована следующим образом

(70)

где определяются следующим образом:

	(71)
	(72)
	(73)
	(74)
	(75)

Динамическая модель в уравнении (70) обладает следующими свойствами, которые используются при последующей разработке:

Свойство 1: Матрица инерции симметрична, положительно определена и удовлетворяет следующим неравенствам [42]

(76)

де - известные положительные константы, а обозначает стандартную Евклидова норму

Свойство 2: Матрицы и кососимметричны в том смысле, что

(77)

Свойство 3: Динамическая модель, приведенная в уравнении (70), может быть линейно параметризована следующим образом [42]

(78)

где содержит неизвестные постоянные системные параметры, и обозначает матрицу регрессии. Формулировка матрицы регрессии уравнения (78) также может быть записана в условиях желаемого контура следующим образом

(79)

где желаемая матрица регрессии определяется

Свойство 4: Производная по времени матрицы преобразования может быть выражена следующим образом [42]

(80)

где обозначает желаемую скорость подачи, а определяется как

(81)

В уравнении является однозначной непрерывной функцией, которая обозначает желаемую кривизну контура, и является однозначной непрерывной функцией, которая обозначает желаемое кручение. Производная по времени уравнения (80) может быть определена как

(82)

Основываясь на предположении, что требуемый контур выбран таким образом, что , , , , , тогда уравнение (80) и уравнение (82) могуть быть использованы для вывода о том, что .

Замечание 1: Частную производную по длине дуги требуемого контура обычно называют формулами Серре-Френе [43,44,45]. Из фундаментальной теоремы пространственных кривых [42], требуемый контур может быть однозначно задан (за исключением положения и ориентации) с помощью однозначных непрерывных функций и .

Замечание 2: Следующие неравенства могут быть выведены из уравнений (71) − (10) и свойства 4

	(83)
	(84)

где m , , 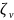, обозначают известные положительные граничные константы.