3.3.3. Формулировка управления

Динамика станка в этом разделе моделируется следующим уравнением

(101)

где обозначает силу трения, а обозначает аддитивное ограниченное возмущение, представляющее силы резания, и

Трение и резание моделируются таким образом, что , и существуют и ограничены при (более подробную информацию о модели трения см. в [45]).

Чтобы облегчить разработку управления, вторая отфильтрованная ошибка отслеживания, обозначаемая , определяется следующим образом

(102)

где − положительный постоянный коэффициент усиления управления, а определяется в уравнении (85). Отфильтрованная ошибка отслеживания не поддается измерению, поскольку выражение в уравнении (102) зависит от . После предварительного умножения уравнения (102) на можно получить следующее выражение

(103)

где использовались уравнения (101) и (85). На основе выражения в уравнении (38) входной крутящий момент управления рассчитывается следующим образом

(104)

где обозначает впоследствии разработанное управляющее условие. Подставляя уравнение (104) в уравнение (103), можно получить следующее выражение

(105)

Чтобы облегчить проектирование , уравнение (40) дифференцируется следующим образом

(106)

Основываясь на уравнении (106) и последующем анализе стабильности, рассчитывается следующим образом

(107)

где производная по времени от уравнения (107) задается как

(108)

После подстановки уравнения (108) в уравнение (106) может быть получена следующая система ошибок с замкнутым контуром

(109)

где обозначает следующий неизмеримый вспомогательный член

(110)

Для облегчения последующего анализа другой неизмеримое вспомогательное слагаемое определяется как

(111)

Производная по времени от уравнения (11) задается следующим образом:

(112)

После сложения и вычитания уравнения (111) система ошибок с замкнутым контуром в уравнении (109) может быть выражена следующим образом

(113)

где неизмеримый вспомогательный член 3 определяется как

(114)

На основе выражений в уравнениях (112) и (112) могут быть разработаны следующие:

(115)

где выбираются как достаточно большие положительные константы.

Разработанный контроллер реализован на фрезерном станке с использованием написанного пользователем сервоалгоритма, предоставляемого Turbo PMAC2 (контроллер). Поскольку система привода подачи x-y на HSM2 представляет собой двумерную контурную систему, параметризация, основанная на направлении подачи (см. рис.49), может быть использована для представления матрицы преобразования координат . Пусть − угол наклона между желаемым вектором скорости и осью x, тогда можно представить как

(116)

Рисунок 49

Для линейного контура матрица R в уравнении (81) является нулевой матрицей. Для кругового контура,

(117)

где − радиус окружности. Для общей двумерной траектории R представляет собой матричную функцию угла наклона .

Для двумерного случая вектор неизвестных постоянных параметров системы, θ в уравнение (85) состоит из , где 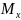 − эквивалентный момент инерции для оси x, − движущаяся масса для оси y, − коэффициент вязкого трения для оси x, а − коэффициент вязкого трения для оси y. Для начальной оценки наилучшего предположения, в уравнении (89), значения, полученные с помощью идентификации системы в используются из предыдущей главы 3.

Учитывая в уравнении (88), пусть будет для простоты. Затемс помощью предыдущих уравнений, может быть выражено следующим образом

	(118)

Ввод управляющего усилия в уравнении (118) может быть описан как компонент с перекрестной связью (т.е. первый набор условий), пропорциональный компонент (т.е. второй набор условий), производный компонент (т.е. третий набор условий) и адаптивный компонент с прямой связью (т.е. четвертый набор условий). Для двумерного кругового контура, уравнение (116) и уравнение (117) может быть использовано для выражения перекрестно связанной составляющей уравнения (118) a

(119)

Поскольку второе и третье слагаемые в уравнении (118) представляют пропорционально-производный (PD) контроллер, для этого используются контроллеры PD, разработанные в предыдущих разделах. Коэффициенты усиления, которые привели к наилучшей производительности в круговых контурах, определяются следующим образом

(120)

Разработанный УЭ нелинейной перекрестной связи представлен на рис. 50.

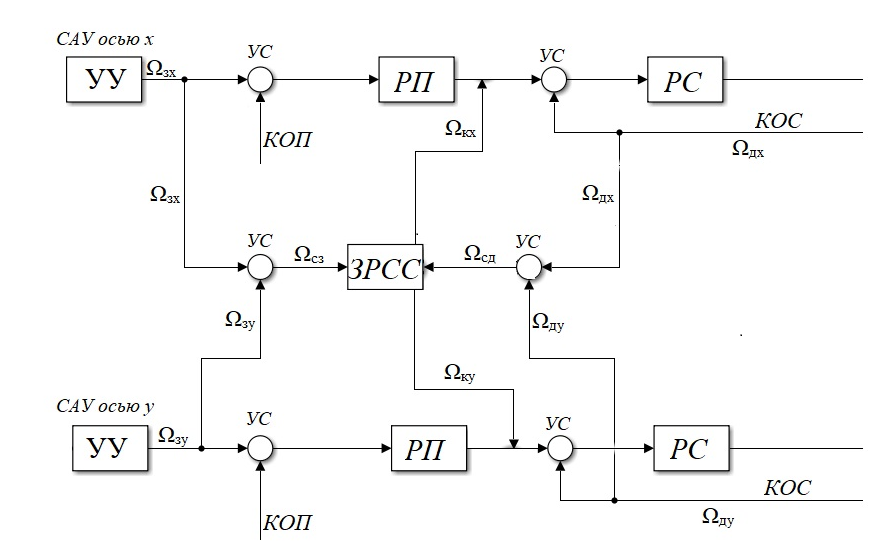
Рисунок 50