3.3.1. Система ошибок замкнутого контура

Система ошибок с разомкнутым контуром для может быть получена путем вычисления производной по времени уравнения (85) и предварительного умножения результирующего выражения на следующим образом

(85)

После использования уравнения (70), уравнения (84) и уравнения (85), может быть получено следующее выражение

(86)

где произведение матрицы линейной регрессии а вектор неизвестных констант , введенный в уравнение (79), задается следующим выражением:

(87)

и вспомогательное выражение определяется как:

(88)

Используя предыдущие уравнения можно разработать следующую верхнюю границу для :

(89)

где 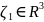− известная положительная ограничивающая константа. Основываясь на уравнении (86) и последующем анализе стабильности, спроектирован следующим образом:

(90)

В уравнении (90), 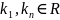обозначают положительные постоянные коэффициенты усиления управления, а обозначает неадаптивную оценку, которая генерируется из следующего дифференциального уравнения:

(91)

где − постоянная диагональная матрица коэффициентов адаптации, а обозначает начальную наилучшую оценку неизвестных параметров в . Система ошибок с замкнутым контуром для может быть получена после замены уравнения (90) в уравнение (86) следующим образом:

(92)

где обозначает несоответствие адаптивной оценки, определяемое следующим образом:

(93)

3.3.2. Анализ стабильности

Теорема 1: При условии, что коэффициент усиления управления 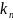выбран в соответствии со следующим достаточным условием

(94)

где 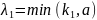, закон управления, приведенный в уравнении(25), обеспечивает глобальное асимптотическое управление отслеживанием в том смысле, что:

(95)

Доказательство: обозначим следующую неотрицательную функцию Ляпунова

(96)

Производная по времени уравнения (96) может быть записана следующим образом

(97)

Основываясь на уравнении (89), для уравнения (97) может быть разработано следующее неравенство

(98)

где был введен в уравнении (94). Следующее выражение может быть получено после заполнения квадратов на заключенных в квадратные скобки членах в уравнении (98)

(99)

При условии, что выбрано в соответствии с достаточным условием, приведенным в уравнении (94), может быть разработано следующее неравенство

(100)

для некоторой положительной константы . Из уравнений (96) и (100) мы можем заключить, что ; следовательно, . Выражения в уравнениях (96) и (100) также могут быть использованы для вывода о том, что 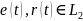. Учитывая, что 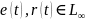, методы линейного анализа могут быть использованы для доказательства того что , из уравнения (85). Поскольку , уравнение (93) можно использовать для доказательства того, что . Предположение о том, что может использоваться вместе с уравнением (82) и уравнением. (83) чтобы сделать вывод о том, что .

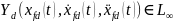Основываясь на этих фактах, уравнения (89) - (92) могут быть использованы для доказательства того, что . Поскольку (т.е. достаточное условие для того, чтобы и были равномерно непрерывными) и , лемма Барбалата может использоваться для доказательства результата в уравнении (95). Поскольку является однозначным преобразованием, уравнения (68) и (69) могут быть использованы для доказательства того, что если результат в уравнении (95) получен, то