3.1.1. Линейная интерполяция

Целью линейной интерполяции является перемещение из одной точки пространства в другую по линейному пути [35,36]. Это показано на рис. 44, где, обозначает начальную точку и обозначает конечную точку. Если задана максимальная скорость подачи 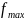, с которой необходимо перемещаться по этому пути, и период замыкания контура управления , который не может быть больше периода интерполяции, движение от до может быть разделено на точек таким образом, что,

(24)

где - общее расстояние, которое необходимо преодолеть по пути. Для случая двумерного линейного пути,

(25)

Осевые приращения (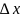 и ) вычисляются как:

(26)

что приводит к увеличению пути,

(27)

и опорные точки на линейном пути генерируются как,

(28)

Для .

Рисунок 44

3.1.2. Круговая интерполяция

Целью круговой интерполяции является перемещение по определенной дуге окружности [35.36], как показано на рис. 45(а). Движение начинается в точке , продолжается по дуге окружности с радиусом r и центральной точкой в точке и заканчивается в точке ,. и - начальный и конечный углы (в радианах) соответственно. Аналогично линейной интерполяции, расстояние между последовательными опорными точками, является постоянным, и поэтому равно ; углу, пройденному на каждом шаге. Количество промежуточных этапов интерполирования рассчитывается как,

(29)

где в этом случае,

(30)

Угловое приращение для каждого шага интерполяции вычисляется как,

(31)

что приводит к расстоянию между последовательными точками в виде,

(32)

С другой стороны, если желательно поддерживать определенную радиальную точность, обозначенную на рис. 45(б), следует обеспечить, чтобы не превышало критического значения 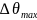. который может быть записан как,

(33)

Рисунок 45

Если это произойдет, максимальная скорость подачи должна быть уменьшена, чтобы привести к меньшим угловым приращениям.

Отныне координаты опорных точек вычисляются как,

(34)

Предлагаемая схема круговой интерполяции включает тригонометрические вычисления на каждом шаге. Хотя в литературе существуют инкрементные методы для выполнения круговой интерполяции с меньшей вычислительной нагрузкой [35,36], этот подход является предпочтительным для поддержания максимально возможной точности интерполяции, что имеет решающее значение для генерации ограниченной траектории. Таким образом, также предотвращаются рывки, возникающие в результате внесения поправок в опорную траекторию, чтобы компенсировать накапливающиеся радиальные отклонения из-за ошибок округления.

3.1.3. Кусочно-линейная интерполяция

Интерполяция кусочно-линейная соединяет узлы N+1 с использованием сплайнов пятого порядка (рис. 46). Полученный сплайн предназначен для обеспечения сохранения непрерывности вплоть до производной второго порядка вдоль общей составной кривой.

Рисунок 46

Сплайн параметризуется с использованием длины хорды между двумя последовательными узлами.

Процедура подгонки начинается с вычисления первой и второй производных для узла путем подгонки кубического многочлена

(35)

через 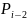, , , . Параметр кубического многочлена может быть однозначно определен с использованием координат четырех последовательных точек , , , . Как только кубическая подгонка получена, первая производная (касательный вектор) и вторая производная (нормальный вектор) для могут быть вычислены. С помощью первой и второй производных от , квинтический сплайн может быть помещен между двумя последовательными узлами ,

(36)

где, … , и … – коэффициенты сплайна, а – параметры сплайна.

Граничными условиями, используемыми для решения параметров сплайна, являются

где – длина хорды между , .