
- •24. Комплексные числа и операции над ними.
- •25. Алгебраические многочлены и их корни.
- •27. Формулы Виета
- •26. Осн теорема алгебры и ее следствие. Теорема о кратности корней алгебраич многочлена.
- •28. Нод. Алгоритм Евклида.
- •29.Теорема Безу. Схема Горнера.
- •30. Разложение рацион дробей на сумму простейших. Метод неопред коэф-тов.
- •32. Теорема о размерности ядра и образа оператора.
- •31. Линейные операторы и их свойства. Обратный оператор.
- •33. Теорема о ранге оператора.
- •34. Матричная запись оператора. Матрица оператора.
- •36. Характеристический многочлен лин оператора. Собст значение и вектор лин операторов.
- •37. Теорема об условии диагональности матрицы лин оператора.
- •35. Преобразование матрицы линейного оператора при переходе к новому базису.
- •38. О линейной независимости собственных векторов лин оператора, отвечающих различн собств значениям.
- •39. Билинейные формы в Евкл пространстве. Теорема о представлении билинейной формы.
- •42. Теорема о матрице билинейной формы.
- •43. Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билин формы.
- •44. Приведение квадратичной формы к канонич виду методом Лагранжа.
- •40. Сопряж операторы в Евклид пространстве. Самосопряж операторы и их свойства.
- •41. Нормы линейн пространства.
- •45. Приведение квадратич формы к канонич виду методом ортогон
- •46. Приведение к канонич виду уравнения кривой 2 порядка. Приведение к канонич виду уравнений поверхности 2 порядка.
41. Нормы линейн пространства.
опр.
![]() V
– евклидово
простр-во,
V
– евклидово
простр-во,
![]() .
.
утв.
Имеет место неравенство ||Ax||<=||A||*||x||
(1);
![]()
Док-во: Ax = A * ((1/ ||x||)*x*||x||)
||(x/ ||x||)|| = 1, т.к. (1/||x||)*||x|| = 1 =>||Ax|| = ||( A* (1/ ||x||)* x* ||x||)|| <= sup ||Az||*||x|| = ||A||*||x||
||Ax|| <= ||A||*||x||, ч.т.д.
утв.2.
А – самосопряж оператор =>
![]() ;
||Ax||
<= ||A||
* ||x||;
|<Ax,x>|
<= ||A|| * ||x||;
;
||Ax||
<= ||A||
* ||x||;
|<Ax,x>|
<= ||A|| * ||x||;
![]() ;=>
μ <= ||A||
=> (1/ ||x||)*
|<Ax,x>|
<= ||A||
* ||x||
;=>
μ <= ||A||
=> (1/ ||x||)*
|<Ax,x>|
<= ||A||
* ||x||
||(x / ||x||) = 1 => |<Ax, (x/ ||x||)>|| <= ||A|| * ||x|| => sup|<Ax,x>| <= ||A||; |A * (x/ ||x||), (x/ ||x||)| <= A => μ = ||A|| => μ = sup |<Ax,x>| = ||A||
утв3.
![]() V
– евклидово
простр-во,
А – самосопряж оператор. λ – собствен
значение А =>
V
– евклидово
простр-во,
А – самосопряж оператор. λ – собствен
значение А =>
![]()
Док-во:
![]() (5).
Обозначимx
= z/
||z||
=> ||x||
= || (z/
||z||
)|| = (1/ ||z||)
* ||z||
= 1. (5) => Az
= A*
(x
||z||)
= λ*x*||z||
=> ||z||*A*x
= λ*x*||z||
=> Ax
= λ*x
= <Ax,x>
= < λx,
x>
= λ <x,
x>
= λ*||x||^2
= λ => λ = <Ax,x>,
||x||
= 1, ч.т.д.
(5).
Обозначимx
= z/
||z||
=> ||x||
= || (z/
||z||
)|| = (1/ ||z||)
* ||z||
= 1. (5) => Az
= A*
(x
||z||)
= λ*x*||z||
=> ||z||*A*x
= λ*x*||z||
=> Ax
= λ*x
= <Ax,x>
= < λx,
x>
= λ <x,
x>
= λ*||x||^2
= λ => λ = <Ax,x>,
||x||
= 1, ч.т.д.
утв4. А – самосопряж оператор, λ – любое собствен значение А.
о пр.
матрица В(е) =
пр.
матрица В(е) =
 ,
где
,
где
![]() -
из (2), наз-ся матрицей линейно формы
В(х,у) в базисе
-
из (2), наз-ся матрицей линейно формы
В(х,у) в базисе![]()
утв.
Любая квадратная матрица
![]() явл-ся
данным в базисе матрицы некоторой
билинейной формы.
явл-ся
данным в базисе матрицы некоторой
билинейной формы.
Док-во:
![]() -
данный базисL;
-
данный базисL;
![]() ,
,![]() ,
,![]() -
данная матрица.
-
данная матрица.![]() .
В(х,у) – билин форма, т.е. удовлетворяет
аксиомам 1-4. В(x+z,
y)
= В(x,y)
+ В(z,y);
.
В(х,у) – билин форма, т.е. удовлетворяет
аксиомам 1-4. В(x+z,
y)
= В(x,y)
+ В(z,y);
![]() =>
В(x+z,
y)
=
=>
В(x+z,
y)
=![]()
![]() В(х,у)
+ В(z,y),
ч.т.д.
В(х,у)
+ В(z,y),
ч.т.д.
утв. В(х,у) – симметричная билинейная форма, если В(е) симметричная матрица (необх и дост условие)

полярной к А(х,х).
 координаты
вектора
координаты
вектора
![]() коэф-ты
у относительно
коэф-ты
у относительно![]() (т.к..
билинейная форма симметрична), а
(т.к..
билинейная форма симметрична), а![]() .
.
![]() матрица
квадратичн формы А(е).
матрица
квадратичн формы А(е).
теорема.
Любая квадратичная форма А(х,х) в n-мерном
лин пространстве L
с помощью невырожденного линейного
преобразования координат может быть
приведена к канонич виду
![]() ,
где
,
где![]() -
координаты вектора
-
координаты вектора![]() канонический
коэф-т.
канонический
коэф-т.
Основная идея метода Лагранжа – последовательно выделяется полный квадрат по каждому аргументу.
Док-во:
А(х,х) не = 0,
![]() в данном базисе
в данном базисе![]()
1
шаг: А(х,х) можно преобразовать так, что
коэф-т при 1-ой координаты вектора х не
=0. Если а11 =0, но другие коэф-ты не =0 =>
при перенумерации базисного вектора
а11 не =0.
![]()
![]()
![]()




пусть
а11 не , в (1) выделим ту группу слагаемых,
кот-е содержит х, т.е.

Преобразуем выделенную сумму
![]()
![]()
(3)
и (4)=>![]() ,
где aij
–
коэф-т после преобразовния
,
где aij
–
коэф-т после преобразовния
![]()
![]() ;
;
![]() преобразуем
преобразуем![]() .
Повторяем этот процесс, получим в итоге
квадратич форму виду
.
Повторяем этот процесс, получим в итоге
квадратич форму виду![]()
45. Приведение квадратич формы к канонич виду методом ортогон


виду 1) метолом Лагранжа 2) методом ортогонал преобразований
Решение:
1)
![]() дополним до полного квадрата
дополним до полного квадрата![]()
![]() ;
;![]()
![]()
Применим
к W(x1,x3),
соберем все члены в группу:
![]()
![]()
![]()
т.о.
получим
![]() ;
;![]() ;
;![]()




 ;
<x2,x3>=-1+1+1=0 => x2┴x1;
<x3,x1>=0; HO <x2,x3>=0,25 => x2 HE ┴
x1
;
<x2,x3>=-1+1+1=0 => x2┴x1;
<x3,x1>=0; HO <x2,x3>=0,25 => x2 HE ┴
x1
собств
вектора
 ;х=Ру:
;х=Ру:
![]() ;
;![]() ;
; ;
; ;
;


Док-во: а11*(х^2)+а12*х*у+а22*(у^2)
A = (a11 a12 = (а11 а12
a21 a22) а12 а22)
привести к канонич виду методом ортогон преобразований.
(х = Р * (х’ Р – ортогон матр= (Р11 Р12
у) y’) (1) Р21 Р22)
λ1*((x’)^2)+ λ2*((y’)^2); λ – собств значение матр А.
столбцами Р явл-ся соответст собств векторы А.
Р – ортогон матрица => (система): (P11)^2 + (P21)^2 = 1; (P12)^2 + (P22)^2 = 1; P11*P12 + P21*P22=0
P11=cos φ; P21= sin φ; P12 = cos ψ; P21 = sinψ
cos φ * cos ψ + sin φ * sinψ =0
cos (φ – ψ)=0 => (φ – ψ)=± (π/4) + πk; φ= ψ – (π/2); cos ψ= cos (φ + (π/2)) = sin φ
P = (cos φ sin φ
sin φ cos φ) -> преобразование поворота на φ
в ОХУ: ĩ, ĵ (базисн векторы) переходит в прямоуг систему ОХ’У c ĩ’, ĵ’ (базисн векторы), причем (ĩ’, ĵ’) = (ĩ, ĵ)Р
i = cos φ * ĩ’ + sin φ * ĵ’
j = - sin φ * ĩ’ + cos φ * ĵ’
через (1) выразим 2*b1*x + 2*b1*y через координаты x’, y’ => λ1 * ((x’)^2) + λ2 * ((y’)^2) + 2*b1*(x’) + 2*b1* (y’) + c =0; выделим полный квадрат относительно x’ и y’: λ1* (x’ + ĩ1)^2 + λ2 * (y’ + ĩ2) + c =0
λ1*(x’’)^2 + λ2* (y’’)^2 + c =0
пр. 11*x^2 – 20*x*y – 4*y^2 20*x – 8*y +1=0 привести к канон виду с помощью

преобразований. Закон инерции квадрат формы.
![]() матрица
квадратичн формы.
матрица
квадратичн формы.
пр.
A(x,x)=![]()
 ;
;
 ;
x=Py
;
x=Py
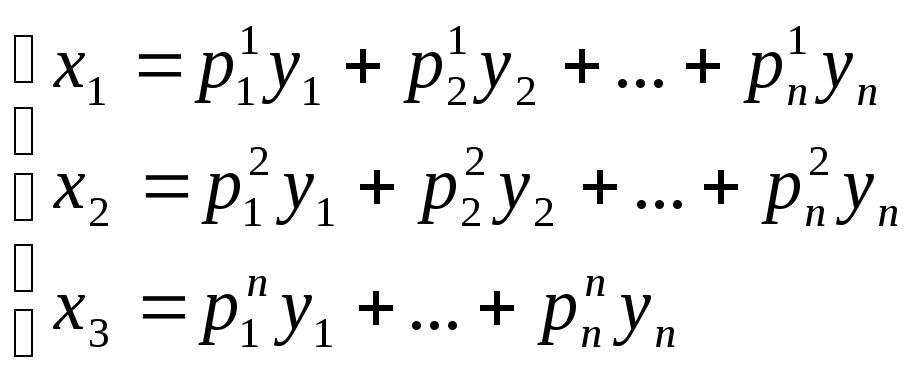 если
матрица Р невырожденная, то
если
матрица Р невырожденная, то
![]() еслиdet
P
=0 (вырожденное линейное преобразование),
х=РУ – ортогон преобразование, если Р
– ортогон матрица, т.е.элементы
строк(столбцов) попарно ортогональны
еслиdet
P
=0 (вырожденное линейное преобразование),
х=РУ – ортогон преобразование, если Р
– ортогон матрица, т.е.элементы
строк(столбцов) попарно ортогональны
![]()
теор.
![]() ортогон
преобразование х=РУ, приводящее ее к
канонич виду,т.е. квадр форме
ортогон
преобразование х=РУ, приводящее ее к
канонич виду,т.е. квадр форме![]() ,
(i=
1…n
– собств знач матрицы А, а столбцы Р –
ортогональные нормированные собств
векторы м-цы А)
,
(i=
1…n
– собств знач матрицы А, а столбцы Р –
ортогональные нормированные собств
векторы м-цы А)
Пр.
![]() привести
к канонич)
привести
к канонич)

2)

![]() ;
rang=2
если λ=-2:
;
rang=2
если λ=-2:
 ;
; ;
;
нормизуем
х1: собств вектор

если
λ=4:
 пусть
х2=1,x3=0
=>x1=0,5:
пусть х2=0, х3=0 =>х1= 0,5
пусть
х2=1,x3=0
=>x1=0,5:
пусть х2=0, х3=0 =>х1= 0,5


![]()
Закон инерции квадратичн формы: независимо от способа приведения квадр формы к канонич виду, число е положительно и число ее положительных, а также отриц-х коэффициентов постоянны.
![]()
![]() (без
док-ва)
(без
док-ва)
