24. Комплексные числа и операции над ними.

опр. комплексные числа – числа вида x+iy, где (упорядоченная пара чисел). х – действительная часть,iy – мнимая часть, i – мнимая единица.

z1=x1+iy1; z2=x2+iy2

“+” z1+z2 = (x1 + x2) + i(y1+y1)

“-“ z1-z2 = (x1 – x2) + i(y1-y2)

“x” z1*z1 = (x1+iy1)(x2+iy2) = (x1*x2 – y1*y2) + i(x1y2 + y1*x2)

z’ = x-iy – сопряженное число z

z*z’ = x^2 + y^2

z1/z2 =

C – множество комплексн чисел.удовлетворяют всем аксиомам линейн пространства.

1)

2) (z1+z2) + z3 = z1 + (z2+z3)

3) z1 + (-z1) = 0 (0=0+i0)

4) λz = λx + i λy

5) (z1 * z2) * z3 = z1 * (z2 ) z3)

C- линейное пространство,

|z|=r=, x=r*cosφ; y=r*sinφ

z= x+iy = r*cosφ + ir*sinφ = r (cosφ + isinφ) = |z| * (cosφ + isinφ); |z| -модуль, φ – аргумент

при k=0

при k=1

имеет n значений (или корней), эти корни расположены на окружности с радиусом = и они являются вершинами правильногоn-угольника, вершина которого наход-ся на этой окружности.

Пр2. x^2 – 2x +6 =0

D= -20, x = 1=> |z| = 5

при k=0 =x1

при k=1 =x2

25. Алгебраические многочлены и их корни.

опр.алгебраическим многочленом n степени назөся выражение: , С1 – комплексное число,z – переменная, комплексн.

пр. Р(х) = ax^2 + bx + c; a не =0.

Любой многочлен в n степени можно делить на любой многочлен в степени, не превосходящей n.

пр. x^4 + 1 = (x^2 + x +1) (x^2 = ) + (x+1)

док-во: (необходимость). Пусть а - корень кратности α для f(z) => a - корень кратности (α-1) для f’(z) => корень кратности (α-2) для f’’(z) =>…=> корень кратности 1 для ,т.е. f(a) = 0, f’(a) = 0,

Кроме того, а не является корнем для многочлена , т.е.

(достаточность) => а - корень кратностине <1 => а - корень кратности не <2 для => … => а - корень кратностине ниже α для f(z) => если а корень кратности > α, - противоречие => теорема доказана.

27. Формулы Виета

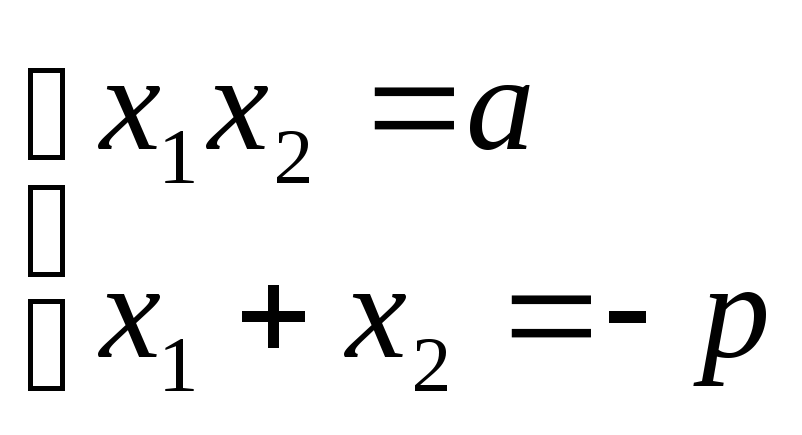
f(x)=xⁿ+a₁x^n-1+a₂x^n-2+…+a_n-1x+a_n, и пусть ₁,…,_n – его корни. f(x)=(x-₁)…(x-_n). Перемножив скобки справа, приводя подобные члены и сравн.получ-е коэфф-ты с коэфф-ми из (1), получаем рав-ва, наз-е формулами Вьета. Эти ф-лы выражают коэффициенты мног-на ч/з его корни:

a₁= -(₁+₂+…+_n),

a₂=₁₂+₁₃+…+₁_n+₂₃+…+_n-1_n,

a3= -(₁₂₃+₁₂₄+…+_n-2_n-1_n),………

a_n-1=(-1)^n-1(₁₂…_n-1+₁₂…_n-2_n+…+₁₂…_n),

a_n=(-1)ⁿ₁_2…_n.

Т.О.: в правой части k-го нер-ва стоит сумма всевозм произв-й по k корней, взятая со знаком «+» или «-», в зависимости от четности или нечетности k.

Если старший коэффициент а₀ мног-на f(x) отличен от 1, для применения ф-л Виета нужно сначала разделить все коэфф-ты на а₀, что не влияет на корни мног-на. Т.О., в этом случае

- остаток = 0

Доказать: - НОД (f(z), φ(z))

1) f(z)/r2(z), φ(z)/:

2) /r0(z), r0(z) – делитель f(z), φ(z)

1) Согласно (к+1) шага => согласно шагу (к), т.к.и, ч.т.д.

2) пусть r0(z) - делитель f(z), φ(z). Доказать

=> r2(z):r0(z) => =>, ч.т.д.

Процесс нахождения НОД – алгоритм Евклида.

пр. f(z)=z^4 – 2z^3 + 3z^2 – 2z +1

φ(z) = 4z^3 – 6z^2 + 6z-2

1 шаг: Делим f(z) на φ(z), получаем остаток (3/4)z^2 – (3/4)z + (3/4), частное (1/4)z-1/8

2 шаг: φ(z)=r1(z) * φ(z) + r2(z).

Делим φ(z) на z^2 – z + 1, частное 4z-2, остаток=0

=> НОД (f(z), φ(z))= z^2 – z + 1

НОД определяется с точностью до постоянного сомножителя

Свойства делимости мног-ов:

1. если f(x) дел-ся на g(x), а g(x) дел-ся на h(x)  f(x) тоже дел-ся на h(x). Д-во: по усл.: f(x)= g(x)*j(х), g(x)= h(x)*(х)  f(x)= h(x)[(х)*j(х)].

2. если f(x) и g(x) дел-ся на j(х) их сумма и разность тоже дел-ся на j(х). Д-во: т.к. f(x)=j(х)*y(х) и g(x)=j(х)*(х)  f(x)g(x)=j(х)[y(х)(х)]

комплексного числа.

опр. Комплексные числа равны, если их действ и мнимые части равны.

tgφ = y/x => φ = actg (y/x)

Пр. z = 1+I => x=1; y=1, |z| = √2; tgφ = 1/1=1 => φ = π/4

z = √2 (cos π/4 + isin π/4)

z1 = r1 (cosφ1 + isinφ1); z2 = r2 (cosφ2 + isinφ2)

z1*z2 = r1*r2 [(cosφ1*cosφ2 – sinφ1*sinφ2) + i*(sinφ1*cosφ2 + cosφ1*sinφ2)] = r1*r2 [cos (φ1+φ2) + i*sin (φ1+φ2)]

z1*z2 = |z1|*”|z2| * (cos (φ1 + φ2) + i*sin (φ1 + φ2))

if z1=z2: z^2 = |z|^2 * (cos 2φ + isin 2φ)

формула Муавра:

показательная формула , формула Эйлера -

формула Муавра в показат форме

Извлечение корня.

z = r (cosφ + isinφ); ;W = ρ (cos ψ +isin ψ) => z = W^n => W^n = (ρ^n) (cos ψ +isin ψ) => r (cosφ + isinφ) = (ρ^n) (cos ψ +isin ψ) => r = ρ; φ+2kπ = nψ k=0,1…(n-1) => ψ = (φ + 2kπ)/n

W =

При извлечении n корня извлекается n корень из модуля, затем [cos…]

Пр.

утв. f(z), φ(z) –многочлены, причем степень φ(z) ≤ степени f(z), тогда f(z) = φ(z)*g(z) + r(z), где g(z) и r(z) – многочлены. Степень g(z) = разности степени f(z) и φ(z), а степень r(z) < степени φ(z).

Вопрос о делимости f(z) на многочлен 1 степени φ(z):

опр. число b является корнем f(z) если f(b)=0, b – комплексн.

Если r(z) (остаток) = 0 => f(z) делится на φ(z)

теор. f(z) делится на (z-b), если b является корнем f(z).

Док-во: (c-const, многочлен в нулевой степени)

пусть φ(z)=z-b => f(z) = φ(z)*g(z) + r(z) = (z-b)*g(z) + r(z) => (r(z)=с) =(z-b)*g(z) + c => r=b f(b) = c =0 => f(z) = φ(z) * g(z) => f(b) = 0, ч.т.д.