1 курс / 1 курс 2 семестр / Теория_вероятностей_15_22_лекц_1К

Теория вероятностей и математическая статистика

Для оценки используют «исправленное» среднее квадратическое отклонение s.

Поскольку обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то теория, изложенная в предыдущем параграфе, применима для оценки точности измерений.

41

Теория вероятностей и математическая статистика

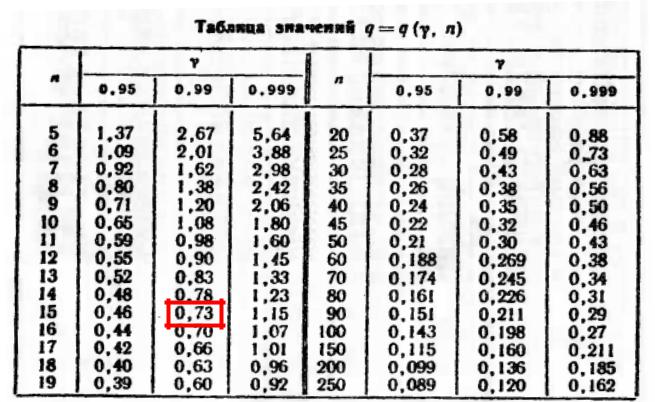
Пример. По 15 равноточным измерениям найдено «исправленное» среднее квадратическое отклонение s = 0,12. Найти точность измерений с надежностью 0,99.

Решение. Точность измерений характеризуется средним квадратическим отклонением случайных ошибок, поэтому задача сводится к отысканию доверительного интервала s(1 — q) < < s(1 + q) (*), покрывающего с заданной надежностью 0,99.

42

Теория вероятностей и математическая статистика

14.17. Оценка вероятности (биномиального распределения) по относительной частоте

Пусть производятся независимые испытания с неизвестной вероятностью р появления события А в каждом испытании. Требуется оценить неизвестную вероятность р по относительной частоте, т. е. надо найти

ее точечную и интервальную оценки.

44

Теория вероятностей и математическая статистика

А. Точечная оценка.

В качестве точечной оценки неизвестной вероятности р принимают относительную частоту

W = m/n,

где m — число появлений события А; n – число испытаний*.

*Напомним, что случайные величины обозначают прописными, а их возможные значения – строчными буквами. В различных опытах число m будет изменяться и поэтому является случайной величиной М. Однако, так как через М уже обозначено математическое ожидание, здесь сохраним для случайного числа появлений события обозначение m.

45

Теория вероятностей и математическая статистика

Эта оценка несмещенная, т. е. ее математическое ожидание равно оцениваемой вероятности.

Действительно, учитывая, что M(m) = nр, получим

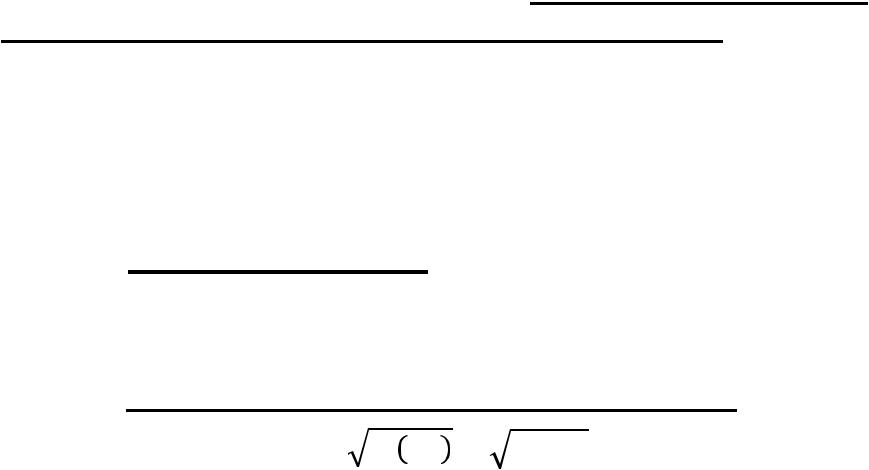
M(W) = M[m/n] = M(m)/n = nр/n = р.

Найдем дисперсию оценки, приняв во внимание, что

D(m) = npq:

D(W) = D[m/n] = D(m)/n2 = npq/n2 = pq/n.

Отсюда среднее квадратическое отклонение

W = = /.

46

Теория вероятностей и математическая статистика

Б. Интервальная оценка.

Найдем доверительный интервал для оценки вероятности по относительной частоте. Напомним, что ранее была выведена формула, позволяющая найти вероятность того, что абсолютная величина отклонения не превысит положительного числа :

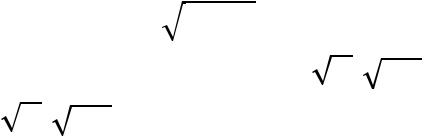
P(| Х - а | < ) = 2Ф( / ), (*)

где X — нормальная случайная величина с математическим ожиданием М(X) = а.

47

Теория вероятностей и математическая статистика

Если n достаточно велико и вероятность р не очень близка к нулю и к единице, то можно считать, что относительная частота распределена приближенно нормально, причем, как показано в пункте А, M(W) = р.

Таким образом, заменив в соотношении (*) случайную величину X и ее математическое ожидание а соответственно случайной величиной W и ее математическим ожиданием р, получим приближенное

равенство*

P(|W – p|< ) = 2Ф( / W). (**)

*так как относительная частота распределена

приближенно нормально

48

Теория вероятностей и математическая статистика

Построим доверительный интервал (p1,p2), который с надежностью покрывает оцениваемый параметр р,

для чего используем рассуждения, с помощью которых был построен доверительный интервал ранее.

Потребуем, чтобы с надежностью выполнялось соотношение P(|W – p|< ) = 2Ф( / W) (**):

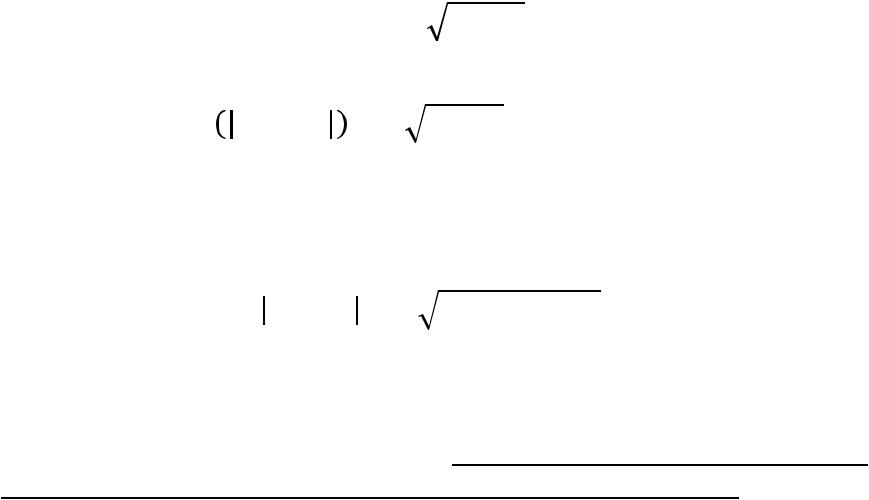
P(|W – p|< ) = 2Ф( / W) = .

Заменив W через / (см. пункт А), получим

P(|W – p|< ) = 2Ф( / ) = 2Ф(t) = ,

где t = / .

49