1 курс / 1 курс 2 семестр / Теория_вероятностей_15_22_лекц_1К

Теория вероятностей и математическая статистика

Однако важно подчеркнуть, что для малых выборок

(n<30), в особенности для малых значений n, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к «повышению

точности оценки».

Например, если n = 5 и = 0,99, то, пользуясь

доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.

21

Теория вероятностей и математическая статистика

То обстоятельство, что распределение Стьюдента при малой выборке дает не вполне определенные результаты (широкий доверительный интервал), вовсе не свидетельствует о слабости метода Стьюдента, а

объясняется тем, что малая выборка содержит малую

информацию об интересующем нас признаке.

22

Теория вероятностей и математическая статистика

14.14. Оценка истинного значения измеряемой величины

Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение а которой неизвестно.

23

Теория вероятностей и математическая статистика

Будем рассматривать результаты отдельных измерений как случайные величины X1, X2, .... Xn. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии 2

(измерения равноточны) и распределены нормально (такое допущение подтверждается опытом).

24

Теория вероятностей и математическая статистика

Тогда, истинное значение измеряемой величины

можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.

Поскольку обычно неизвестно, следует пользоваться формулами предыдущего параграфа 14.13.

25

Теория вероятностей и математическая статистика

Пример. По данным девяти независимых равноточных измерений физической величины найдены среднее арифметической результатов отдельных измерений х = 42,319 и «исправленное» среднее квадратическое отклонение s = 5,0. Требуется оценить истинное значение, измеряемой величины с надежностью =

0,95.

Решение. Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке математического ожидания (при неизвестном ) при помощи доверительного интервала

надежностью = 0,95.

26

Теория вероятностей и математическая статистика

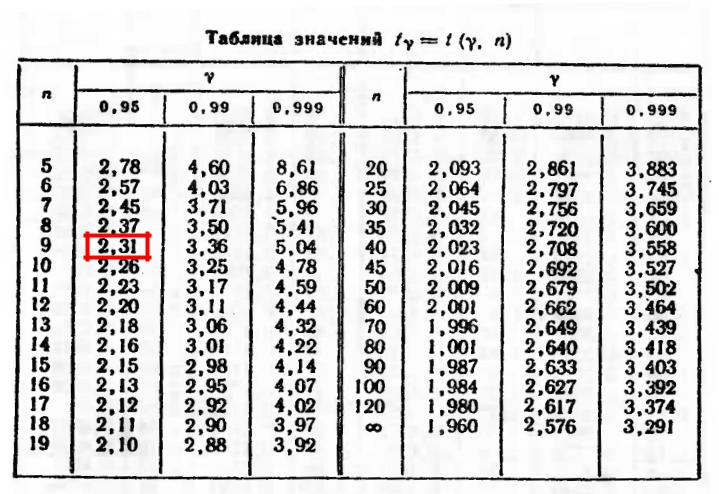
Пользуясь таблицей приложения 3, по =0,95 и n = 9 находим t = 2,31.

Приложение 3

27

Теория вероятностей и математическая статистика

Найдем точность оценки ( = t / ):

= ( / ) = 2,31 (5/ 9) = 3,85.

Найдем доверительные границы:

− = 42,319 — 3,85 = 38,469;

+ = 42,319 + 3,85 = 46,169.

Итак, с надежностью 0,95 истинное значение измеряемой величины заключено в доверительном интервале

38,469 < а < 46,169.

28

Теория вероятностей и математическая статистика

14.15. Доверительные интервалы для оценки среднего квадратического отклонения

нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально. Требуется

оценить неизвестное генеральное среднее квадратическое отклонение по «исправленному»

выборочному среднему квадратическому отклонению s.

Для этого поставим задачу: найти доверительные интервалы, покрывающие параметр с заданной надежностью .

29

Теория вероятностей и математическая статистика

Потребуем, чтобы выполнялось соотношение

Р(| — s|< ) = или P(s — < < s + ) = .

Для того, чтобы можно было пользоваться готовой таблицей, преобразуем двойное неравенство

s — < < s +

в равносильное неравенство

s(1 — /s) < < s(1 + /s)

Положив /s = q, получим

s(1 — q) < < s(1 + q). (*)

30