
Учебники 80377
.pdf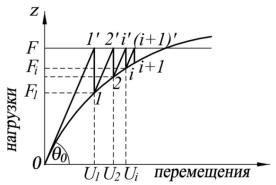
изображает нелинейную связь между перемещениями U и внешней нагрузкой F в соответствии с физическими условиями задачи. Примем линейный оператор Е0=tgθ0, соответствующий начальному модулю упругости (начальным деформационным параметрам системы). Точка 1´ на пересечении координат F, U1 изображает начальное упругое решение задачи. В действительности перемещениям U1 на части расчётной области соответствует нагрузка F1 (точка 1). Элементы расчётной области (каждый, где это требуется, в отдельности) разгружаются от напряжений, вызванных силами ∆F1=F–F1. Условия задачи выполнены, но образовалась невязка сил ∆F1. Затем (в соответствии с кусочной диаграммой 1´–1–2´ на рис. 35) расчётная область (в целом) нагружается этими силами (но противоположного направления), приложенными в тех же точках, сохраняя при этом начальный линейный оператор Е0.
Рис. 35. Схема итерационного процесса метода упругих решений
В общем виде восходящая ветвь итерационного процесса МУР на одной ступени итерации описывается условным уравнением
Е0 (Ui+1–Ui)=F–Fi . (2.47)
В научной литературе известно ещё одно название этого метода: метод начальных напряжений (МНН).
Рассмотрим процедуру МУР-МНН на примере задачи о совместном растяжении силой F=300 кН нитей А и В, объединённых диском С (рис. 36, а). Диск С закреплён от поворота и поперечного смещения и свободно перемещается в направлении силы F. Диаграммы δ=f(FА,В) растяжения нитей изображены на рис. 35, б. Нить А растягивается упруго без предела текучести; нить В растягивается в соответствии с билинейной диаграммой с пределом текучести 100 кН. Жёсткости обеих нитей (до достижения предела текучести нитью В) равны. Решение задачи очевидно: сила F=300 кН распределяется между нитями на 200 кН (нить А) и 100 кН (нить В).
Получим тот же результат при помощи решения задачи методом упругих решений.
Вначале получим линейное решение: сила F=300 кН распределяется между нитями А и В поровну – FА=FВ=150 кН. Этот результат противоречит усло-
79
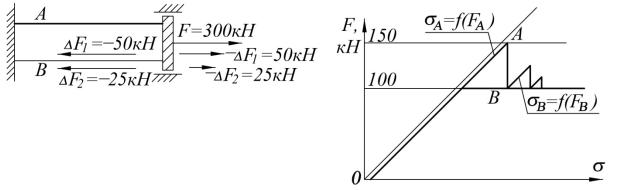
вию задачи о пределе текучести нити В на уровне FВ=100 кН. Приложим к нити В сжимающую силу ∆F=–50 кН. Теперь условия задачи соблюдены, но имеет место невязка силы ∆F1=–50 кН. Чтобы её компенсировать, увеличим силу F на 50 кН и приложим её в той же точке, что и сила F=300 кН.
а) |
б) |
Рис 36. Схема (а) и диаграммы u=f(FА,В) (б) к задаче о совместном растяжении нитей А и В
Разделим дополнительную силу –∆F1=50 кН между нитями А и В в соответствии с решением линейной задачи на равные части по 25 кН. Теперь FА=150+25=175 кН, FВ=150–50+25=125 кН; часть продольной силы, которую неспособна воспринять нить В, составляет 25 кН. К нити В прикладывается сжимающая сила ∆F=–25 кН. Теперь невязка силы ∆F2=–25 кН. Чтобы её компенсировать, увеличим силу F на величину –∆F2=25 кН. После деления ∆F2=25кН между двумя нитями на равные части, получим FА=150+25+12.5=187,5 кН, FВ=150–50+25–25+12,5=112,5 кН.
Процесс можно продолжить. После каждой новой ступени расчёта (итерации) невязка силы уменьшается в два раза: ∆F3=–12,5 кН, ∆F4=–6,25 кН и т. д.; силы FА и FВ становятся ближе к своим конечным значениям 200 и 100 кН.
Рассмотренный пример показывает, что на каждой (i-й) ступени итерационного процесса МУР вычисления выполняются в два шага.
1.Выявляется пластическая подобласть (в рассмотренном примере – нить В), в которой нагрузки (напряжения), полученные на предыдущей ступени расчёта, превышают предел текучести. На пластическую подобласть накладываются силы, переводящие её в физически возможное напряжённое состояние. Определяется невязка силы.
2.Устранение невязки силы: те же силы, но с противоположным знаком, прикладываются ко всей расчётной области.
При расчётах континуальных (плоских, пространственных) систем «не-
вязка сил» {∆F}i в узлах КЭ образуется из «невязки напряжений» {∆σ}i на его континууме на i-й ступени итерации при помощи матричного соотношения
{∆F}i=∫[B]T{∆σ}idV, |
(2.48) |
80 |
|
где V, [B]T – объём пространственного КЭ (или произведение площади S на толщину t плоского КЭ) и транспонированная матрица соотношений Коши.
Получаемые при этом векторы {∆Ui} накапливаются и складываются с начальными перемещениями упругого расчёта. Расчёт доводится до значений {∆Ui} или {–∆Fi}, близких к нулю. Параметры {∆Ui} или {–∆Fi} удобно использовать в качестве меры невязки.
Главными достоинствами МУР являются ясность физического содержания и постоянство в процессе расчёта начальной «упругой» матрицы жёсткости системы. Это качество иллюстрирует параллельность наклонных отрезков диаграмм на рис. 35 и 36,б.
Недостаток метода – не всегда быстрая сходимость итерации. Наиболее известный способ ускорения сходимости – использование повышающих коэффициентов к невязкам напряжений и сил.
Например, если в рассмотренной выше задаче о растяжении нитей А и В к невязке силы ∆F1=–50 кН применить повышающий коэффициент 2,0, то получим ∆F1=–50×2=–100 кН. Повторив те же действия, что и ранее, получим FА=150+100/2=200 кН, FВ=150–100+100/2=100 кН. Решение с нулевой невязкой
получено за одну ступень итерации.
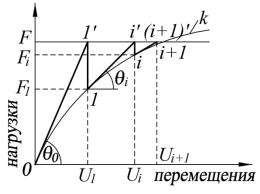
Метод Ньютона–Рафсона (рис. 37) является развитием МУР. Его отличие заключается в определении (в зависимости от достигнутого уровня деформации) и использовании на каждой (i+1)-й ступени итерации переменных деформационных параметров Еi=tgθi.
Лучи 0–1´, 1–i´, изображающие на рис. 37 зависимости между приращениями перемещений ∆Ui+1=Ui+1–Ui и нагрузками F–Fi, являются касательными к кривой 0–1–i–(i+1). Вычислительную схему метода Ньютона–Рафсона характеризует следующее условное уравнение восходящей ветви одной ступени итерации:
Еi (Ui+1– Ui)=F–Fi . |
(2.49) |
Рис. 37. Схема к математической процедуре метода Ньютона-Рафсона
Метод Ньютона–Рафсона позволяет ускорить сходимость за счёт сокращения числа ступеней итерации, но на каждой ступени необходимо заново строить матрицу жёсткости. При этом в соотношениях [D] связи деформаций и напряжений теряется симметрия, и нулевые члены, отражающие в законе Гука
81
независимость объёмного деформирования от формоизменения, заменяются значащими числами.
2.6.Заключительные замечания. Ключевые положения МКЭ
Внастоящей разделе изложено описание линейной версии МКЭ на основе уравнений, постулатов и понятийного аппарата строительной механики и теории упругости. Обобщением основных идей, математических процедур,
приёмов их алгоритмизации являются следующие ключевые положения МКЭ. 1. Конечный элемент – «область тела в совокупности с заданными в ней
аппроксимирующими функциями» [11] перемещений.
Разделение сплошной среды на конечные элементы (КЭ) не сопровождается разрывами на контактах. Задача решается так, что условие неразрывности выполняется не только в узлах, но и на границах КЭ. Это положение не относится к полям относительных деформаций и напряжений, разрывы (скачкообразные изменения) которых на границах КЭ не только возможны, но в большинстве случаев неизбежны.
Одним из показателей качества численного решения является абсолютная или относительная величина этих разрывов. Чем она меньше, тем выше качество решения.
2.Основными принципами, определяющими уравнениями, на которых основано решение задач теории упругости средствами МКЭ, являются следующие положения: 1) условия равновесия узлов конечно-элементной системы; 2) закон Гука; 3) геометрические соотношения Коши, выражающие непрерывность и относительную малость перемещений; 4) описание перемещений в континуальных КЭ при помощи некоторых функций, из которых чаще всего используются степенные полиномы; 5) вариационный принцип минимума для перемещений Лагранжа.
3.В качестве основного способа решения задач МКЭ используется метод перемещений:
– канонические уравнения выражают равновесие узлов;
– неизвестными канонических уравнений являются перемещения узлов.
4.При расчёте систем, состоящих из плоских и пространственных (трёхмерных) конечных элементов, все силы должны быть приложены в узлах.
5.Каждый член матрицы жёсткости КЭ Kij выражает реакцию (узловую силу) в закреплении по направлению i-й степени свободы (считая это закрепление неподвижным) на единичное перемещение Uj по направлению j-й степени свободы.
6.При расчётах стержневых и континуальных систем каждый КЭ находится в глобальной и местной системах координат.
Нумерация узлов в местной системе является общепринятой и используется по умолчанию для каждого типа КЭ. Первый узел помещается в начало координат местной системы. Примеры нумерации других узлов: в стержневом
82
КЭ второй узел совпадает с концом стержня; в треугольном КЭ узлы номеруются последовательно против часовой стрелки, в прямоугольном КЭ сначала номеруются нижние два узла слева направо, затем верхние два узла слева направо.
Контрольные вопросы для самопроверки
1.Опишите наиболее известные формы конечных элементов.
2.Охарактеризуйте степени свободы узлов конечных элементов:
–стержневых плоских и пространственных;
–плоских треугольных и прямоугольных;
–осесимметричных;
–тетраэдров и параллелепипедов.
3.Назовите компоненты напряжений в плоских, пространственных и осесимметричных конечных элементах.
4.Дайте определение коэффициента в составе матрицы жёсткости конечного элемента.
5.Опишите матрицу жёсткости стержневого конечного элемента с тремя степенями свободы в узле.
6.Объясните понятия о континууме, континуальных конечных элементах, функциях перемещений.
7.Объясните построение матриц жёсткости треугольного и прямоугольного плоских конечных элементов.
8.Что представляют собой общая и глобальная системы координат и какова их роль в схеме решения задач МКЭ?
9.Опишите формирование глобальной системы уравнений на примере фрагмента расчётной области, состоящей из прямоугольных и стержневых плоских конечных элементов.
10.Охарактеризуйте конечные элементы, моделирующие связи конечной жёсткости.
83
3. СМЕШАННАЯ (УПРУГОПЛАСТИЧЕСКАЯ) ЗАДАЧА ТЕОРИЙ УПРУГОСТИ И ПЛАСТИЧНОСТИ. НЕЛИНЕЙНЫЙ РАСЧЁТ ГЕОТЕХНИЧЕСКИХ ОБЪЕКТОВ
3.1. Упругопластическая задача для грунтов (постановка и решение)
Модель грунта. В условиях современного проектирования наиболее эффективной и востребованной является рассматриваемая ниже упругопластическая модель грунта, сочетающая использование четырёх групп уравнений:
1) закона Гука (для допредельной стадии деформирования); 2) соотношений Коши; 3) условий текучести (предельного напряжённого состояния) в соответствии уравнениями Мора-Кулона или Мизеса-Шлейхера-Боткина; 4) кинематических соотношений теории пластического течения.
Условия |
|
|
Равновесие узлов системы МКЭ. Принцип Лагранжа |
|||||||||||||||||||
равновесия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Физические |
|
|
Уравнение |
|
|
|
Закон Гука |
|
|
Уравнение Мизеса - |
||||||||||||
уравнения |
|
|
Мора - Кулона |
|
|
|
|
|
|
|
Шлейхера - Боткина |
|||||||||||
|
|
|
Закон Кулона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
(для заданных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
поверхностей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
сдвига) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Геометриче- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ские и кине- |
|
|
|
|
|
|
|
|
|
Соотношения Коши |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
матические |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кинематические соотношения |
|
|
|
|
|
|
||||||||||
соотноше- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ния |
|
|
|
|
|
|
теории пластического течения |
|
|
|
|
|
|
|||||||||
Расчетные |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Смешанная (упругопластическая) задача теорий |
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||
модели |
|
|
|
|
|
|
упругости и пластичности |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Плоская |
|
|
|
|
|
|
|
Пространственная и |
|
|||||||||
|
|
|
деформация |
|
|
|
|
|
|
|
|
осесимметричная |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
задача |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 38. Структурная схема упругопластической модели грунта
На рис. 38 представлена структурная схема РМ, сочетающей уравнения теорий линейно деформируемой и жёстко-пластической сред, которые прошли длительный отбор и многократную проверку при проектировании различных
84
категорий сооружений. Получаемое по расчёту напряжённо-деформированное состояние является физически возможным во всех точках. Геометрической иллюстрацией (двухмерной аналогией) упругопластической РМ является диаграмма Прандтля в виде линии 3 на рис. 21.
Постулаты и гипотезы, формирующие принятую модель грунта, и описывающие их уравнения для условий плоской деформации, пространственной и осесимметричной задач представлены в табл. 9.
Для подготовки исходных данных при решении смешанных задач теорий упругости и пластичности требуется шесть параметров каждого слоя грунта: удельный вес γ, модуль деформации Е, коэффициент поперечной деформации ν, угол внутреннего трения φ, удельное сцепление с, параметр дилатансии Λ* или
Λ. Для пространственной (осесимметричной) задачи параметры φ и с заменяются другой парой: α≈(sinφ)/3 и k≈ccosφ.
Решение упругопластической задачи. Задача решается средствами МКЭ в сочетании с рассмотренной выше процедурой метода упругих решений по версии «метода начальных напряжений» (МНН).
Введём следующие обозначения: {σ}={σx σy σz τxy τyz τxz σ1 σ2 σ3}, {ε}={εx εy εz γxy γyz γxz ε1 ε2 ε3} – матрицы-строки компонентов напряжений и относительных деформаций в точке (элементарном объёме грунта), конечном элементе или центре конечного элемента. Те же матрицы, содержащие члены с верхним индексом «е» ({σе}, {εе}), означают результаты линейного (упругого) решения задачи. Матрица {σр} содержит компоненты напряжений, удовлетворяющие физическим условиям задачи; при этом одно из условий выполняется на предельном уровне: Fp=0, где Fp – правая часть уравнений, описывающих предельное напряжённое состояние.
Предположим, что на некоторой части расчётной области по результатам линейного расчёта получено распределение напряжений, не удовлетворяющее одному из условий прочности. Его необходимо «исправить», т.е. получить на всей расчётной области физически возможное напряжённое состояние, которое может быть допредельным (Fe<0) или предельным {σр}, определяемым в зависимости от {σе} и соответствующим условию Fp=0.
Учитывая, что грунты слабо сопротивляются растяжению, при котором теряет силу закон сопротивления сдвигу и снижается модуль деформации, будем считать их работающими только на сжатие. Поэтому, если в линейном решении {σе} получено σ1е>0, то принимается σ1р=0. При этом второе главное напряжение должно удовлетворять условиям одноосного
сжатия грунтов:
0 ≥σ2е ≥ –2c cosφ/(1–sinφ).
.
85
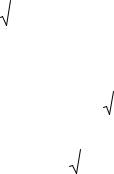
86
Таблица 9
Описание упругопластической модели грунта
Характеристика РМ |
|
|
|
Плоская деформация |
|
|
|
Осесимметричное |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
напряженное состояние |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Учитываемые проявления |
1. Пластическое формоизменение при сложном напряженном состоянии |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Деформирование без сопротивления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
нелинейности грунта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Сдвиг по заданной (контактной) поверхности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Зависимость между напряжения- |
Билинейная в соответствии с диаграммой 3 на рис. 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ми и деформациями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения закона Гука для ли- |
σx |
|
|
|
E |
|
|
|
|
1−ν |
|
|
ν |
0 |
|
εx |
σx |
|
|
|
|
|
|
|
1−ν |
|
ν |
|
ν |
|
|
|
|
|
|
0 |
εx |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
ν |
1−ν ν |
|
|
|
|
|
|
0 |
|
||||||||||
нейной части деформации |
σz |
= |
|
|
|
|
|
|
|
ν |
|
1−ν |
0 |
|
εz |
σz |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εz |
||||||
|
+ν)(1−2ν) |
|
|
|
|
|
|
|
|
|
|
ν |
|
ν |
1−ν |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
+ν)(1−2ν) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
(1 |
|
|
|
|
|
|
1−2ν |
|
σθ |
(1 |
|
|
|
|
|
0 |
εθ |
|||||||||||||||||||||||
{σ}= [D]{ε} |
τxz |
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
γxz |
τ |
|
|
|
|
|
|
0 |
0 |
|
|
0 |
|
1−2ν |
γ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
xz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
xz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Уравнение Мора-Кулона |
|
Уравнение Мизеса-Шлейхера- |
||||||||||||||||||||||||||||||||||||||
Уравнение предела текучести |
|
|
|
|
|
|
|
Боткина |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
(σ1 −σ2) |
|
(σ1 +σ2) |
|
|
|
|
|
|
|
|
+αI1 − K = 0 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
F = |
+ |
sinϕ−c cosϕ =0 |
|
|
|
|
I2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Уравнения для пластических |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ1,2,3 |
− |
|
I1 |
|
|
|
|||||||
|
|
|
|
ε п |
|
= λ (Λ |
|
±1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
1,2 |
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
деформаций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε1,2,3 = λ (Λ+ |
|
|
|
|
|
|
|
|
) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Дилатансионные соотношения на |
|
|
|
|
Λ |
|
= |
ε1п |
+ ε 2п |
|
|
|
|
|
|
|
|
Λ = |
|
J1п |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
ε1п |
− ε 2п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
стадии пластического течения |
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
J2п |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Природное давление в основа- |
|
|
|
|
σ 1,2 |
= р = −γ z1 |
|
|
|
|
|
|
σ1,2,3 |
= р = −γ z1 |
|
|
|
|||||||||||||||||||||||||
нии, ограниченном горизонталь- |
(z1– координата глубины основания, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
ной плоскостью |
отсчитываемая от его поверхности) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
86
Графической иллюстрацией связей между σ1,2е и σ1,2р я вляются схемы на
плоскости главных напряж ений (рисунок 39), где линия ВС изображает уравнение Мора-Кулона Fp=0, то чка В – напряжённое состояние σ1 =0, σ2=–2ccosφ/(1– sinφ). При σ1е>0, 0 ≥σ2е ≥ –2c cosφ/(1–sinφ) принимается σ1р=0, σ2р=σ2е (точки 1 и
1´). При σ1е>0, σ2е>0 принимается σ1р=0, σ2р=0 (точки 2 и 2´). При σ1е>0, σ2е<–2c cosφ/(1–sinφ) прин имается σ1р=0, σ2р=–2ccosφ/(1–sinφ) (точки 3 и 3´).
Рис 39. Графическая форма связей между σ1,2р и σ1,2е на плоскости главных напряжений
При пространственном напряжённом состоянии зависи мости, связывающие напряжения σ2е и σ2р, распространяются на σ3е и σ3р.
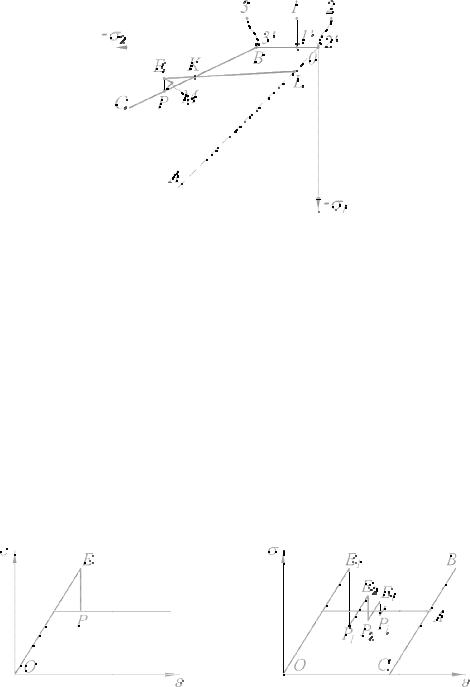
Наибольшее практи ческое значение имеет случай, когда исходное напряжённое состояние {σе} явл яется всесторонне сжимающим, но не удовлетворяет условию текучести в соот ветствии с уравнениями Мора-Кулона (1.7) или Мизе- са-Шлейхера-Боткина (1.1 7): Fe>0. Для составления уравнений связи между {σе} и {σр} воспользуемся условием, согласно которому «упр угие» деформации {εе}, вызываемые напряжениями {σе}, равны упругопластическим деформациям от напряжений {σр}. Это равенство иллюстрирует рисунок 40, а, где на билинейном графике ε=f(σ) точка Е изображает напряжённо-деформированное состояние {σе}–{εе}, а точка Р – напряжения {σр}, которые требуется определить.
а) 
 б)
б)
Рис. 40. Графические иллюстрации:
а– к уравнениям (3.1); б – к уравнениям (3.13), (3.14)
87
Кроме того, в расчёт вводится условие о коаксиальности (соосности) тен- зоров-девиаторов напряжений и скоростей пластических деформаций, следствием чего является соосность напряжений σ1,2,3е и σ1,2,3р. Это позволяет записать следующие уравнения для условий плоской деформации:
|
|
1 |
|
|
[(1−ν )σ |
e |
−νσ |
e |
|
|
|
1 |
|
[(1−ν )σ1 |
p |
−νσ |
p |
|
1 |
|
λ(Λ |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
] = |
|
|
|
|
|
|
2 |
]+ |
|
|
|
+1), |
|
||||||||||||||||
|
|
|
|
|
|
|
2G |
|
|
2G |
|
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1) |
||||||
|
|
1 |
|
|
|
|
|
|
e −νσ |
e |
|
|
|
|
1 |
|
|
|
|
|
|
|
p −νσ |
p |
|
|
1 |
|
|
|||||||||||||
|
|
|
|
[(1−ν )σ |
|
] = |
|
|
[(1−ν )σ |
|
]+ |
λ(Λ |
|
−1), |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
2 |
1 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
2G |
|
|
|
|
|
|
|
|
|
|
2G |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где G = |
|
|
E |
|
– модуль сдвига; Е, ν, λ, Λ* сохраняют значения, принятые в п. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
2(1+ν ) |
|
|||||||||||||||||||||||||||||||||||||||||
1.4. Левые части |
уравнений |
(3.1) |
|
|
выражают |
относительные деформации |
||||||||||||||||||||||||||||||||||||
ε |
e = |
1 |
[(1−ν )σ |
|
e −νσ |
|
e ], |
|
|
|
|
|
первые |
|
|
|
|
|
члены |
|
|
|
|
правых |
частей |
|||||||||||||||||
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1.2 |
2G |
|
|
|
|
2,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ε |
p = |
|
1 |
[(1−ν )σ |
|
p −νσ |
p ] |
– «упругие» части главных деформаций от на- |
||||||||||||||||||||||||||||||||||
|
|
1,2 |
||||||||||||||||||||||||||||||||||||||||
|
1.2 |
|
2G |
|
|
|
|
|
2,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
пряжений {σр}, вторые члены |
ε |
|
|
|
n = |
|
|
1 |
λ(Λ |
|
±1) |
– пластическую деформацию |
||||||||||||||||||||||||||||||
1,2 |
|
2 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
формоизменения c дилатансией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Неизвестные главные напряжения должны удовлетворять условию теку- |
|||||||||||||||||||||||||||||||||||||||||
чести |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F p = |
σ1 p −σ2 p |
|
+ |
σ1 p +σ2 p |
sinϕ − ccosϕ = 0. |
|
|
(3.2) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
22
Уравнения (3.1) и (3.2) образуют замкнутую систему, решение которой позволяет получить следующие соотношения связи между σ1,2р и σ1,2е:
|
λ = Fe |
|
|
|
|
1− 2ν |
|
; |
|
(3.3) |
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
G(1− 2ν + Λ sinϕ) |
|
|
||||||||
|
|
p |
|
e |
|
|
|
e |
1− 2ν ± Λ |
|
|
|||
σ |
1,2 |
|
= σ1,2 |
F |
|
|
|
|
|
, |
(3.4) |
|||
|
1 |
− 2ν + Λ sinϕ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fe |
= |
σ1e −σ2e |
+ |
σ1e |
+σ2e |
sinϕ − ccosϕ . |
(3.5) |
|||||||
|
|
|
||||||||||||
22
Вконечных элементах пластической области Fе>0.
Вернёмся к рис. 39, где на плоскости главных напряжений пограничная прямая линия ВKРС изображает уравнение Мора-Кулона Fp=0, пунктирная ли-
88
