
Учебники 80377
.pdf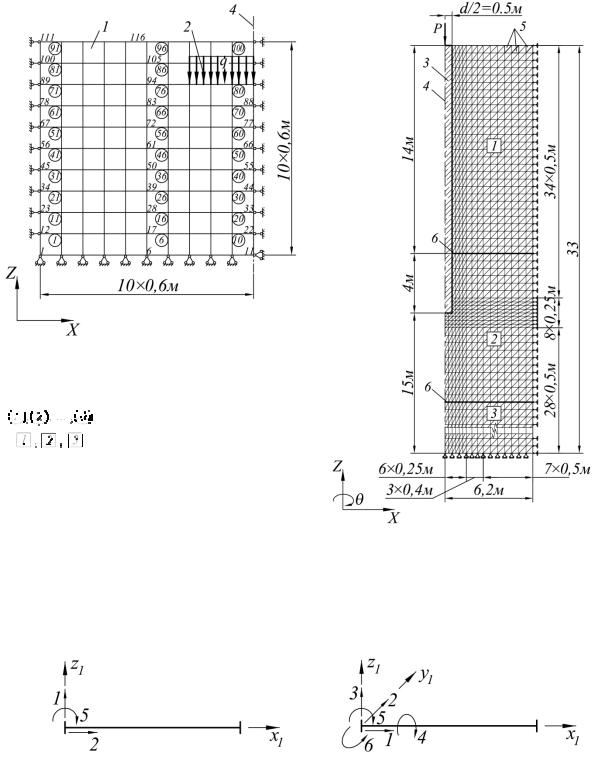
а) |
б) |
1, 2, 3…100 – номера узл ов, 

























 – номера КЭ,
– номера КЭ,
– номера ин женерногеологически х элементов
Рис. 24. Примеры член ения расчётных схем (областей) на конечные элементы:
а – фрагмент полупространст ва, плоская деформация (прямоугольные КЭ); б – осесимметричная система (тело вращения) – свая круглого сечения, вдавливаемая в грунтовое основание осевой силой; стенка; 1 – пластинчатые КЭ, 2 – полосовая нагруз ка, 3 – буронабивная свая, 4 – плоскость (ось) симм етрии; 5 – кольцевой КЭ треугольного сечения, 6 – границы геологических слоёв
а) |
б) |
Рис. 25. Пл оский и пространственный стержневые КЭ с тремя (1, 2, 5) и шестью (1, 2, 3, 4, 5, 6) степенями свобод ы в узле
При идеализации п лоских и сплошных тел (сред) прилегающие друг к другу КЭ считаются шарнирно скреплёнными в узлах. Поэто му в узлах расчётных областей, напряжённ о-деформированное состояние кото рых соответствует условиям плоской задачи приняты степени свободы по направлениям осей X и
49

Z. Результатом расчёта таких систем являются нормальные σx, σz и касательные τxz компоненты напряжений (рисунок 26,а). В пространственных системах возможны перемещения по направлениям осей X, Y, Z, и в расчёте определяются все шесть компонентов напряжений: σx, σy, σz, τxy, τxz, τyz (рис. 26,б).
На рис. 24,б изображено продольное сечение осесимметричной расчётной области (тела вращения) с кольцевыми КЭ треугольного сечения. Каждый узел такой системы имеет две степени свободы по направлениям X и Z, угловое перемещение относительно оси Z отсутствует. Определяемые компоненты напряжений (рис. 26,в) – σx, σz, σθ, τxz. Так как по векторам степеней свободы рассматриваемая задача не отличается от плоской, то и решается по аналогичной процедуре.
Как будет показано в дальнейшем, деление сплошных тел (сред) на КЭ не сопровождается разрывами на контактах. Задачи решаются так, чтобы условие совместности перемещений выполнялось не только в общих узлах, но и на границах КЭ. Поля перемещений в сплошных упругих (линейно деформируемых) телах (средах) являются непрерывными (согласованными), а поля деформаций, напряжений, углов поворота могут иметь (и чаще всего имеют) разрывы на границах КЭ.
а)
б) |
в) |
Рис. 26. Примеры плоских, пространственных и осесимметричного конечных элементов: а – плоские треугольные трёх- и шестиузловой КЭ, прямоугольные четырёх- и восьмиузловой КЭ с двумя степенями свободы в узле; б – пространственные КЭ: тэтраэдр и параллелепипед с тремя степенями свободы в узле; в – осесимметричный КЭ (фрагмент тела вращения) треугольного сечения с двумя степенями свободы в узле; 1, 2, 3 – векторы степеней свободы.
50
Связь МКЭ с методом перемещений. Наиболее известный проектировщикам и исследователям, применяемый в строительной механике вариант МКЭ основан на процедуре метода перемещений. Уравнения, связывающие перемещения узлов на концах (вершинах) КЭ и силы, действующие по направлениям этих перемещений, известны из теории и определены заранее. Эти соотношения формируют общую (глобальную) систему уравнений, выражающую равновесие сил и неразрывность перемещений в общих узлах контактирующих КЭ. Расчёт заключается в формировании и решении системы уравнений, неизвестными в которой являются перемещения свободных от связей узлов.
Применительно к стержневым расчётным схемам рассматриваемый способ реализации МКЭ может рассматриваться как матричная форма метода перемещений, отличающаяся долее глубокой формализацией алгоритма в связи
его ориентацией на использование ЭВМ.
Связь МКЭ с теорией упругости: общность и различия. В математической теории упругости существует ограниченное число решённых задач даже для однородных расчётных областей. Практическая значимость и привлекательность МКЭ связаны с возможностью получать решения научных и технических задач с любыми граничными условиями и такими усложняющими факторами как физическая неоднородность, взаимодействие с заделанными в ли- нейно-деформируемую среду стержневыми элементами, внутренние разрывы сплошности.
Как известно, в теории упругости используются три группы определяющих уравнений:
–закон равновесия в форме дифференциальных соотношений частных производных внутренних напряжений;
–линейные геометрические соотношения Коши связи между перемещениями и деформациями, выражающие непрерывность и относительную малость перемещений;
–линейные физические уравнения (закон Гука) связи между напряжениями и относительными деформациями.
Кроме того, полученные решения должны удовлетворять уравнениям совместности Сен-Венана, выраженным через относительные деформации или напряжения.
В МКЭ (в отличие от теории упругости) статическое равновесие представлено уравнениями метода перемещений, выражающими равновесие узлов. Равновесие узловых сил и напряжений внутри КЭ описывается энергетически-
ми соотношениями по принципу Лагранжа со следующей формулировкой. Принцип Лагранжа. Если некоторое упругое тело находится в равнове-
сии под действием внешних сил, то из всех мыслимых вариаций перемещений материальных точек этого тела действительными являются те, при которых потенциальная энергия системы (т. е. тела и приложенных к нему сил) будет иметь стационарное (минимальное) значение.
51
В настоящем учебном пособии доказательство принципа Лагранжа не приводится, и основанные на нём соотношения МКЭ записываются без вывода.
Геометрические соотношения Коши используются в МКЭ в своей классической записи в соответствии с уравнениями (1.19) и (1.22).
В МКЭ уравнения закона Гука используются в обратной записи: напряжения определяются в зависимости от деформаций. Причина этого станет понятной при чтении п. 2.2.4. Матричная форма соотношений закона Гука, принятая в МКЭ, приводится в табл. 7.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 7 |
|||
Матричная форма уравнений закона Гука, принятая в МКЭ |
|
|
|
|||||||||||||||||||||||||||||||
Вид напряжён- |
|
|
|
|
|
|
|
|
|
|
|
Записи уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ного состояния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общий случай, |
σ x |
|
|
|
|
|
|
|
|
|
|
1−ν |
|
ν |
|
ν |
0 |
|
|
|
0 |
|
|
|
|
0 |
|
ε x |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
пространст- |
|
|
|
|
|
|
|
|
|
ν |
1−ν |
|
ν |
0 |
|
|
|
0 |
|
|
|
|
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
венное |
σ y |
|
|
|
|
|
|
|
|
|
|
ν |
|
ν |
1−ν |
0 |
|
|
|
0 |
|
|
|
|
0 |
|
ε y |
|
||||||
напряжённое |
σ z |
|
|
|
|
E |
|
|
0 |
0 |
|
|
0 |
1− 2ν |
|
|
0 |
|
|
|
|
0 |
|
ε z |
|
|||||||||
состояние |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
τ xy (1+ν )(1− 2ν ) |
|
|
|
|
|
|
|
|
|
1− 2ν |
|
|
|
|
|
γ xy |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
τ xz |
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
γ xz |
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− 2ν |
|
|
|||||||
|
τ yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ yz |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
0 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Плоская |
|
|
|
|
|
σ x |
|
|
|
|
|
|
|
|
1−ν |
ν |
0 |
|
|
ε x |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
деформация |
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
σ z |
= |
|
|
|
|
|
|
|
ν |
1 |
−ν |
0 |
ε z |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
+ν )(1− 2ν ) |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
(1 |
|
|
|
1− 2ν |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
τ xz |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
γ xz |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Осесимметрич- |
|
|
|
σ x |
|
|
|
|
|
|
|
|
1−ν |
ν |
|
ν |
|
|
0 |
|
|
ε x |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ное напряжён- |
|
|
|
|
|
|
|
|
|
|
|
ν |
|
1−ν |
|
ν |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
0 |
|
|
ε z |
|
|
|
|||||||||||
|
|
|
|
σ z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ное состояние |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
ν |
|
ν |
|
1−ν |
|
|
0 |
|
|
ε |
|
|
|
|
|||||
|
|
|
|
|
(1+ν )(1− 2ν ) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
σ |
θ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− 2ν |
|
|
θ |
|
|
||||||||
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
|
|
|
|
γ |
xz |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
xz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.2.Матрицы жёсткости конечных элементов
2.2.1.Общие положения
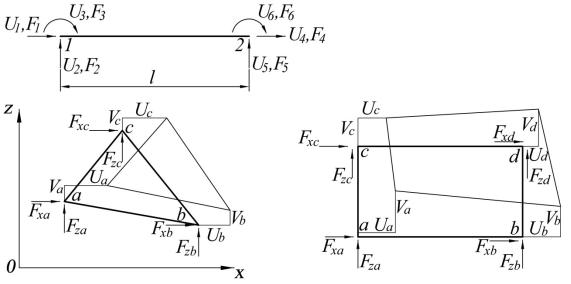
Рассмотрим построение матриц жёсткости КЭ, не касаясь пока вопроса о том, как они используются для решения задач МКЭ. Покажем это на примерах (рис. 27,а,б,в) стержня общего вида с тремя степенями свободы (связями) на концах, треугольного и прямоугольного КЭ плоской (плоское напряжённое состояние или плоская деформация) системы с двумя степенями свободы в каждой вершине.
52
а)
б) |
в) |
Рис. 27. Плоские конечные элементы (а – стержень общего вида, б – треугольник, в – прямоугольник), перемещения и узловые силы на их концах и вершинах
Предполагается, что действующие силы приложены только в узлах (1, 2 на рис. 27,а; a, b, с, d на рис. 27,б,в) и приведены к направлениям перемещений. Матрица жёсткости КЭ содержит коэффициенты уравнений, связывающих векторы сил и перемещений узлов по направлениям координатных осей.
2.2.2.Матрица жёсткости стержневого КЭ
Вобщем виде связь между перемещениями U1…U6 и узловыми силами F1…F6 (см. рис. 26,а) с постоянной жёсткостью растяжении-сжатии ЕА и изгибе EI выражается матричным соотношением
|
|
|
{F}=[K]{U}, |
|
|
(2.1) |
||
где |
|
|
|
|
|
|
|
|
|
|
F |
|
|
U |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
F2 |
|
|
U 2 |
|
|
|
|
|
F |
|
{U } |
U |
|
|
(2.2) |
|
{F }= 3 |
, |
= |
3 |
, |
|||
|
|
F4 |
|
|
U 4 |
|
|
|
|
|
F |
|
|
U |
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
F6 |
|
|
U 6 |
|
|
|
− векторы-столбцы сил и перемещений, |
|
|
|
|
|
|||
|
K11 |
K12 |
K13 |
K14 |
K15 |
K16 |
|
|
|
|
|||||||
[K]= |
K21 |
K22 |
K23 |
K24 |
K25 |
K26 |
(2.3) |
|
|
... ... ... ... ... ... |
|
||||||
|
K61 |
K62 |
K63 |
K64 |
K65 |
K66 |
|
|
53
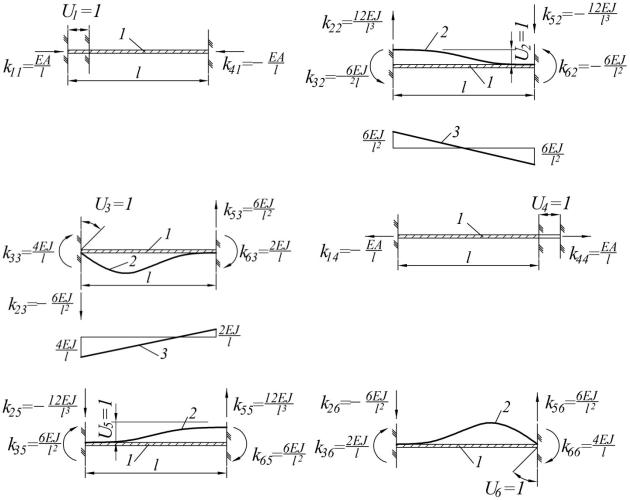
− матрица жёсткости КЭ. Каждый коэффициент Kij выражает реакцию (уз-
ловую силу) в закреплении по направлению i-й степени свободы (считая это закрепление неподвижным) на единичное перемещение Uj=1.
На рис. 28 показаны возможные перемещения Uj=1 (j=1…6) и вызывае-
мые ими силы Kij в закреплениях на концах стержня. Так, например, при U1=1
(рис. 28,а) K11=EA/l, K21=0, K31=0, K41=−EA/l, K51=0, K61=0. При U3=1 (рисунок 28,в) K13=0, K23=−6EI/l2, K33=4EI/l, K43=0, K53=6EI/l2, K63=2EI/l.
а) б)
в) |
г) |
д) |
е) |
Рис. 28. К построению матрицы жесткости стержня общего вида с шестью закреплениями на концах; а…е – усилия в закреплениях при перемещениях U1… U6; 1 – первоначальное положение стержня; 2 – деформированная ось; 3 – эпюра моментов
54
Полная запись системы уравнений (2.1), включающей матрицу жёсткости КЭ, имеет вид:
|
|
|
|
EA |
|
|
|
0 |
|
|
|
0 |
|
− |
EA |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
l |
12EI |
|
|
6EI |
|
l |
|
|
12EI |
|
|
6EI |
|
|
|
|
|
|||||||||||||||
F1 |
|
|
|
|
0 |
− |
|
0 |
− |
− |
|
|
U |
1 |
|
||||||||||||||||||||||
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
l 2 |
|
|
|
|
|
|||||||
F2 |
|
|
|
0 |
− |
6EI |
|
4EI |
|
0 |
|
|
6EI |
|
2EI |
|
|
U |
2 |
||||||||||||||||||
F3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|||||||||||
= |
|
|
l2 |
|
|
l |
|
|
|
|
l 2 |
|
|
l |
|
|
3 |
||||||||||||||||||||
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. (2.4) |
|||
F4 |
|
|
|
− |
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
U |
4 |
|
|||||||||||
F |
|
|
|
l |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
U |
|
|
|||||||||||||
5 |
|
|
|
|
|
− |
12EI |
|
6EI |
|
|
12EI |
|
6EI |
|
|
|
5 |
|
||||||||||||||||||
F6 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
6 |
||||
|
|
|
|
l |
3 |
|
|
|
|
l |
2 |
|
|
|
|
|
l |
3 |
|
|
|
|
|
l |
2 |
|
|
|
|||||||||
|
|
|
|
|
0 |
− |
6EI |
|
|
2EI |
|
|
0 |
|
|
6EI |
|
|
4EI |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
l2 |
|
|
l |
|
|
|
|
l 2 |
|
|
l |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Аналогичным |
|
путём |
|
осуществляется |
построение |
матриц |
жёсткости |
||||||||||||||||||||||||||||||
стержневых элементов с другими условиями закрепления концов.
2.2.3. Функции перемещений континуальных конечных элементов
Перейдём к рассмотрению матриц жёсткости плоских континуальных КЭ на рис. 27, б, в, в которых коэффициенты Kij по-прежнему обозначают реакции в закреплениях при единичных перемещениях узлов. Для того, чтобы выразить коэффициенты Kij через геометрические и физические характеристики конечных элементов, вводится допущение о форме уравнений (аппроксимирующих функций) для компонентов перемещений.
Выбор аппроксимирующих функций обусловливают следующие требования, которые станут понятными из последующего изложения:
1)количество коэффициентов в степенных полиномах, описывающих компоненты перемещений, должно быть равно числу степеней свободы (определяемых перемещений узлов) КЭ;
2)неразрывность перемещений не только в узлах, но и на границах КЭ; для этого показатели степеней членов полиномов должны быть на единицу
меньше числа узлов, скрепляющих контактирующие КЭ.
Здесь используется математическое правило о том, что через п точек можно провести одну кривую, изображающую полином (п–1) порядка, а через две точки – одну прямую.
Покажем построение функций перемещений на примерах простейших КЭ (трёхузлового треугольника и четырёхузлового прямоугольника) континуальных систем.
55
Треугольный КЭ. Для треугольного КЭ с шестью степенями свободы (см. рис. 27, б) вид функции перемещений представляет собой следующие записи:
u=α1+α2x+α3z, v=α4+α5x+α6z, |
(2.5) |
где u=u(x,z), v=v(x,z) – перемещения в произвольной точке с координатами x и z; α1…α6 – неизвестные пока коэффициенты, способ определения которых излагается ниже.
Введём обозначения (см. рис. 27, б): Ua, Ub, Uc, Va, Vb, Vc – перемещения узлов треугольного КЭ по направлениям координатных осей X, Z; xa, xb, xc, za, zb, zc – координаты узлов a, b, c. Уравнения (2.5) становятся определёнными, если коэффициенты αk (k=1…6) выражены через перемещения и координаты узлов a, b, c, которые используются в качестве граничных условий.
Поскольку записи (2.5) распространяются на вершины треугольника, можно записать:
Ua = α1 +α2 xa +α3 za ;
Ub = α1 +α2 xb +α3 zb ;
Uc = α1 +α2 xc +α3 zc ;
. (2.6)
Va = α4 +α5 xa +α6 za ;
Vb = α4 +α5 xb +α6 zb ; Vc = α4 +α5 xc +α6 zc .
В матричной форме уравнения (2.6) имеют вид:
Ua |
|
1 |
xa |
||
|
|
|
|
xb |
|
Ub |
|
|
1 |
||
U |
|
|
1 |
x |
|
c |
|
= |
|
|
c |
Va |
|
|
0 |
0 |
|
V |
|
|
0 |
0 |
|
b |
|
|
|
|
|
Vc |
|
|
0 |
0 |
|
za |
0 |
0 |
0 |
|
α1 |
|
|
|
|
|
|||||||
zb |
0 |
0 |
0 |
|
α2 |
|
||
z |
c |
0 |
0 |
0 |
|
α |
|
|
|
|
|
|
|
3 |
. |
(2.6*) |
|
0 |
1 |
xa |
za |
|
α4 |
|
|
|
0 |
1 |
xb |
zb |
|
α5 |
|
|
|
|
|
|
xc |
zc |
|
|
|
|
0 |
1 |
|
α6 |
|
|
|||
Помещая начало координат в узел а и принимая xа=0, zа=0, находим решение системы уравнения (2.6):
56
α1 |
= U a ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
α2 |
= |
|
|
|
1 |
[(zb − zc )Ua + zcUb − zbUc ]; |
|
|||||||||||||
2S |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
α |
|
= |
[(x |
|
− x |
|
)U |
|
− x |
U |
|
+ x |
U |
|
]; |
|
||||
3 |
|
|
|
c |
b |
a |
b |
c |
|
|||||||||||
|
|
|
|
|
2S |
|
|
|
c |
|
b |
|
|
(2.7) |
||||||
α4 |
= Va ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
[(zb − zc )Va + zcVb − zbVc ]; |
|
||||||||||||||
α5 |
= |
|
|
|||||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α6 |
= |
1 |
[(xc − xb )Va − xcVb + xbVc ], |
|
|
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
2S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где S=½[(xa–xb)(za–zc)−(xa–xc)(za–zb)]=½(xbzc−xczb) – площадь треугольника.
В треугольных КЭ сплошность контакта на границах обеспечена в связи с линейным распределением перемещений. Поскольку смежные КЭ скреплены в двух узлах, то и смежные грани, проходящие через эти узлы, после деформиро-
вания остаются на одной (общей) прямой.
Прямоугольный КЭ. Для четырёхузлового прямоугольного КЭ с восьмью степенями свободы (см. рис. 27, в) функции перемещений записываются в
следующем виде: |
|
u=α1+α2x+α3z+α4xz, v=α5+α6x+α7z+α8xz, |
(2.8) |
где обозначения u=u(x,z), v=v(x,z), x, z, а также αk, сохраняют те же значения, что в уравнениях (2.5).
Повторим изложенный выше способ определения коэффициентов αk для прямоугольного КЭ на рис. 26, в, принимая координатные функции в виде уравнений (2.8).
Отметим, что и в этом случае соблюдается равенство числа неизвестных коэффициентов αk (k=1…8) и степеней свободы узлов. Перемещения на границах распределены линейно, т. е. требование их совместности (непрерывности) выполняется.
Матричная форма уравнений для перемещений узлов имеет следующий
вид:
Ua |
|
|
xa |
za |
xa za |
α1 |
|
Va |
|
xa |
za |
xa za |
|
α5 |
|
||||||||||||
1 |
1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ub |
= |
1 |
xb |
zb |
xb zb |
α |
2 |
|
, Vb |
= |
1 |
xb |
zb |
xb zb |
|
α6 |
.(2.8*) |
||||||||||
Uc |
1 |
xc |
zc |
xc zc |
α3 |
Vc |
1 |
xc |
zc |
xc zc |
|
α7 |
|||||||||||||||
U |
|
1 |
x |
d |
z |
d |
x |
d |
z |
d |
α |
|
|
V |
|
1 |
x |
d |
z |
d |
x |
d |
z |
d |
|
α |
|
d |
|
|
|
|
|
|
|
4 |
d |
|
|
|
|
|
|
|
8 |
|
|||||||||
57
Системы уравнений (2.8) так же, как (2.6), разрешимы относительно αk. Для прямоугольного КЭ с началом координат в узле а решение имеет следующий вид:
α1 |
= Ua ; |
|
|
|
|
|
|
|
||||||
α2 |
= |
|
Ub −Ua |
|
|
|
|
|||||||
|
; |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
Uc |
−Ua |
|
|
|
|||||||
α3 |
= |
; |
|
|
|
|||||||||
|
|
|
|
m |
|
|
|
|
|
|
||||
α |
|
= |
|
Ud +Ua −Ub −Uc |
; |
|
||||||||
4 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
lm |
|
|
(2.9) |
α5 |
= Va ; |
|
|
|
|
|
|
|
||||||
−Va |
|
|
|
|
|
|
|
|||||||
|
|
|
Vb |
|
|
|
|
|
|
|||||
α6 |
= |
|
|
; |
|
|
|
|
||||||
|
|
|
|
l |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
α7 |
= |
Vc −Va |
|
|
|
|
|
|
|
|||||
|
; |
|
|
|
|
|||||||||
m |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Vd +Va −Vb −Vc |
|
|
|||||||||
α8 |
= |
, |
|
|
||||||||||
|
|
|
|
|
lm |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
где l и m – стороны прямоугольника на рис. 27,в.
В табл. 8 представлены формы и функции перемещений наиболее известных плоских и пространственных КЭ, используемых в расчётах конструкций и оснований. Минимальное число узлов (возможные перемещения которых являются степенями свободы) соответствует числу вершин геометрических фигур. Такие КЭ занимают первые пять строк таблицы. Количество неизвестных коэффициентов αk равно удвоенному (в плоских и осесимметричном КЭ) и утроенному (в пространственных КЭ) числу вершин. Функции перемещений являются полиномами первых степеней координат.
Последние две строки занимают примеры КЭ с удвоенным (по сравнению с минимальным) числом узлов. Функции перемещений в таких КЭ построены на основе многочленов второй степени каждой из переменных. Возможно дальнейшее повышение степени многочленов и увеличение числа узлов (степеней свободы) КЭ. Усложнение КЭ (увеличение числа узлов и повышение порядка уравнений, описывающих перемещения) позволяет повысить точность решения, т. е. эквивалентно увеличению частоты членения расчётной области.
58
