
Учебники 80377
.pdf
Диаграммы 1 и 2 являются ветвями общего графика 3 (диаграммы Прандтля), моделирующего деформирование идеализированного упругопластического тела, которое является универсальной расчётной моделью тео-
рий упругости и пластичности.
Теории линейного деформирования. Первая РМ (линия 1 на рис. 21) представляет собой теорию линейно деформируемой среды, описываемую физическими уравнениями закона Гука и геометрическими соотношениями Коши.
Линейно деформируемые тела в отличие от упругих не восстанавливают деформаций при разгрузке (понимаемой как возвращение к исходному напряжённо-деформированному состоянию). Поскольку при проектировании объектов строительства разгрузка, как правило, не предполагается, указанное различие не препятствует применению теории упругости при расчётах оснований, грунтовых и взаимодействующих с грунтом объектов.
Границей линейного деформирования является предел текучести (точка А), принимаемый для грунтов в соответствии с уравнениями Мора-Кулона (1.7) или Мизеса-Шлейхера-Боткина (1.20)–(1.21). Получение на части расчетной области «зоны (подобласти) разрушения» («физически невозможного» напряжённого состояния), где не удовлетворяются условия прочности в соответствии с указанными уравнениями, свидетельствует о неполной корректности или даже непригодности линейного метода расчета.
В современном проектировании существуют и развиваются два направления решения задач теории линейно деформируемой среды: классическое – с использованием решений математической теории упругости (как правило, в виде готовых таблиц) и индивидуальные численные расчёты по методу конечных элементов (МКЭ).
Ещё одной разновидностью линейной модели является метод местных упругих деформаций (метод коэффициента постели), предназначенный для решения контактных задач расчета изгибаемых конструкций (свай, шпунтовых стенок, плит фундаментов конечной жёсткости), взаимодействующих с грунтом оснований. В
дальнейшем изложении этот метод не рассматривается.
Модели жёстко-пластических сред. Вторая теория представляет собой группу РМ в виде жёстко-пластических тел (сред), описываемых уравнениями предельного равновесия или предельного напряженного состояния и изображённых на рис.21 линией 2. При проектировании геотехнических объектов с использованием моделей рассматриваемой группы применяются уравнения закона Кулона и условие прочности Мора-Кулона. Предполагается, что линейная (упругая) часть перемещений (деформаций) пренебрежимо мала по сравнению с пластической составляющей. В расчетах учитываются только прочностные характеристики грунтов (с, ϕ), задачи решаются как статически определимые. Перемещения остаются неопределенными и не вычисляются, так как жёстко-
39
пластическая РМ не содержит соотношений, связывающих напряжения и деформации.
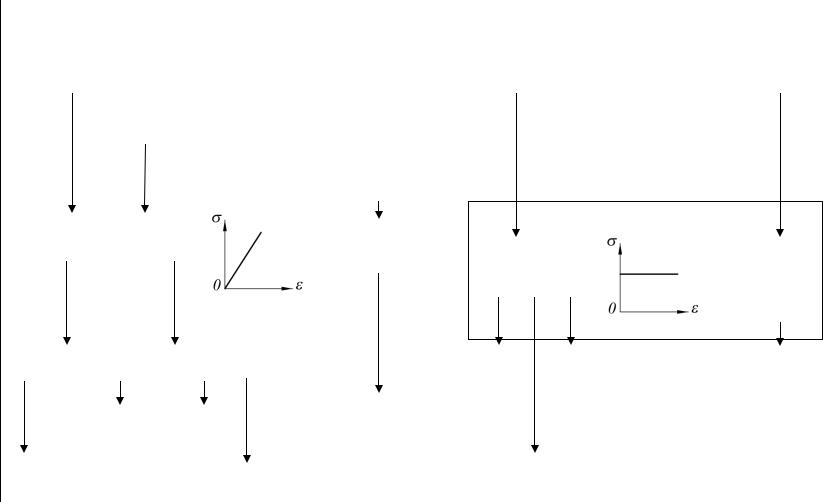
На рис. 22 показаны структурные схемы линейной и жёстко-пластической РМ, изображающие наборы формирующих эти модели уравнений равновесия, физических, геометрических соотношений. В нижней части структурных схем показаны связи РМ с прикладными задачами и практическими приложениями.
Указанные РМ несовместимы по принятым допущениям и используемым механическим характеристикам грунтов. Их упрощенный характер объясняется тем, что напряженно-деформированное состояние предполагается только допредельным на всей расчетной области, подчиняющимся закону Гука и соотношениям Коши; либо предельным. Несмотря на это, применяемые раздельно уравнения теорий линейного деформирования и предельного равновесия (напряжённого состояния) позволили создать комплекс достаточно эффективных методов расчета по предельным состояниям (ПС), предназначенных для проек-
тирования среднесложных геотехнических объектов массового строительства.
Предельные состояния и расчётные проверки норм проектирования.
Основные положения по расчётам объектов строительства на силовые воздействия нормативно закреплены в национальном стандарте Российской Федерации ГОСТ 27751-2014*. Указанный ГОСТ включает основные понятия и определения (в том числе приведенное выше определение ПС), которые формируют современную методологию технических расчётов в строительстве.
Стандарт предусматривает расчёты объектов строительства по ПС трёх групп:
–первая группа – состояния строительных объектов, превышение которых ведёт к потере несущей способности строительных конструкций;
–вторая группа – состояния, при превышении которых нарушается нормальная эксплуатация строительных объектов, исчерпывается ресурс их долговечности или нарушаются условия комфортности;
–особые предельные состояния – состояния, возникающие при особых воздействиях и ситуациях, превышение которых приводит к разрушению зданий и сооружений с катастрофическими последствиями.
____________________________________________________________
*ГОСТ 27751-2014 Надёжность строительных конструкций и оснований. Основные положения.
40
Условия
равновесия
Физические
уравнения
Геометрические
соотношения
Нестрогие
постулаты
Расчётная
модель
41
Прикладные
задачи
Практические
приложения
|
|
|
Дифференциальные уравнения равновесия. |
|
|
Равновесие тела обрушения и его частей (отсеков). |
||||||||||||||||||||||||||||
|
|
Принцип Лагранжа, равновесие узлов системы МКЭ |
|
|
|
|
|
Предельное напряженное состояние в точке |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Закон Гука |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Закон Кулона |
|
Уравнение Мора-Кулона |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношения Коши |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линейные соотноше- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния σ X (Z ) |
= C X (Z )YX (Z ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Жёстко-пластическая среда |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Линейно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Метод коэффи- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
деформируемая среда |
|
|
|
|
|
циента постели |
|
|
|
|
Теория |
|
|
|
|
|
Теория |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
предельного |
|
|
|
|
|
предельного |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равновесия |
|
|
|
|
|
напряженно- |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
го состояния |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Задача Фламана |
|
|
Задача Буссинеска |
|
|
|
|
|
Задачи о |
Метод кругло- |
Расчеты осно- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
подпор- |
|
цилиндрических |
|
ваний по |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных |
|
поверхностей |
|
несущей |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет свай и свай- |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стенках |
|
скольжения |
|
способности |
|
||||||||||||||
|
|
|
Расчеты осадок и кренов |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
ных фундаментов на |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
совместное действие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
вертикальной, гори- |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Начальная крити- |
|
|
|
|
|
|
|
Метод горизонтальных |
|
|
|
|||||||||||||||||||||||
|
|
Метод угло- |
|
|
|
|
|
|||||||||||||||||||||||||||
|
ческая нагрузка |
|
|
|
зонтальной |
сил и |
|
|
|
|
|
сил Г.М. Шахунянца |
|
|
|
|
||||||||||||||||||
|
|
на основание |
|
|
|
вых точек |
|
момента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 22. Линейная и жёстко-пластическая модели механики грунтов:
связи с определяющими уравнениями, прикладными задачами и практическими приложениями (структурная схема)
41
Таблица 6
Главные расчётные проверки оснований, фундаментов, откосных сооружений и их связь с видами предельных состояний
и расчётными моделями
Наименование |
Группы и виды ПС |
Расчётная |
|
расчётов (проверок) |
модель грунта |
||
|
|||
|
|
|
|
Расчёт несущей спо- |
Первая группа: |
Жёстко-пластическая |
|
собности оснований |
-пластическое или хрупкое |
среда: предельное на- |
|
разрушение; |
пряженное состояние |
||
Расчёт устойчивости |
-потеря устойчивости с пере- |
Жёстко-пластическая |
|
оснований и откосов |
ходом в изменяемую систе- |
среда: предельное |
|
против глубокого и |
му; |
||
равновесие |
|||
оползневого сдвига |
-ползучесть, сдвиг, образова- |
||
Расчёт несущей спо- |
ние трещин, ведущие к пре- |
Предельное равнове- |
|
кращению эксплуатации. |
сие при вдавливании / |
||
собности свай |
|
выдергивании сваи |
|
|
|
||
Расчёт устойчивости |
Первая группа: |
|
|
против опрокидыва- |
Предельное равнове- |
||
ния и сдвига фунда- |
-потеря устойчивости с пере- |
сие |
|
ходом в изменяемую систему |
|||
мента |
|
|
|
Расчёт осадок, кренов |
Вторая группа: |
|
|
фундаментов мелкого |
-достижение предельных де- |
Линейно деформи- |
|
заложения |
формаций, прогибов, поворо- |
руемая среда |
|
тов, предельных осадок |
|
||
|
|
||
|
Первая группа: |
|
|
|
-пластическое или хрупкое |
|
|
Расчёт свайных фун- |
разрушение; |
|
|
даментов на совмест- |
-ползучесть, сдвиг, образова- |
|
|
ное действие верти- |
ние трещин, ведущие к пре- |
Метод коэффициента |
|
кальных, горизон- |
кращению эксплуатации. |
постели |
|
тальных сил и мо- |
Вторая группа: |
|
|
ментов |
-достижение предельных де- |
|
|
|
формаций, прогибов, поворо- |
|
|
|
тов, предельных осадок. |
|
42
Описания видов ПС изложены в ГОСТ 27751-2014 в наиболее общем виде, непригодном для использования при проектировании. Их конкретизацией являются расчётные проверки, отражающие предупреждаемые (расчётами) формы разрушения и деформирования, способы их математического описания.
В табл. 6 показана связь между главными нормируемыми расчётными проверками современных сводов правил, расчётными моделями линейного деформирования, предельного равновесия и предельного напряжённого состояния геотехнических объектов и видами ПС в соответствии с формулировками стандарта.
1.5.2. Нелинейные модели грунта
Общие положения. В рассмотренных ранее РМ геотехнических объектов используется только одна группа физических уравнений: либо уравнения закона Гука, либо условия предельного равновесия по закону Кулона (предельного напряжённого состояния грунта в соответствии с уравнением Мора-Кулона). Распределение напряжений на всём континууме расчётной области предполагается либо соответствующим решению теории линейно деформируемой среды, либо предельным.
Вдействительности в большинстве расчётных областей одновременно существуют напряжённые состояния обоих типов. Для того чтобы это положение отразить в расчёте, требуется решение физически нелинейной задачи механики грунтов.
Всовременном строительном проектировании расширяется область использования нелинейных методов расчёта на математической основе МКЭ. Это связано с растущим числом объектов, которые могут быть качественно запроектированы только при помощи решений строгой теории. Примерами таких объектов являются следующие разновидности сооружений:
– крупномасштабные (высотные, большепролетные) сооружения с тяжелыми нагрузками на несущие конструкции и основания;
– сооружения в сложных инженерно-геологических условиях, когда упрощённые расчётные схемы недостаточны для обоснования проектных решений;
– объекты в аварийном или предаварийном состояниях;
– объекты с высокими или повышенными требованиями к точности расчета перемещений (в частности осадок оснований);
– неизученные технические решения.
Но главной предпосылкой востребованности нелинейных (упругопластических) методов расчёта является их доступность (чего не было раньше) в связи
суспехами компьютерной и вычислительной техники.
Использование нелинейных методов предполагает выполнение расчётов по предельным состояниям первой и второй группы без изменения модели грунта. Это позволяет (в отличие от упрощённых методов расчёта) не прибегать
43
к ограничению действующих нагрузок для обеспечения корректности способа определения расчётных напряжений, получать во всех точках физически возможное (допредельное или предельное) напряжённое состояние.
Физически нелинейные задачи строительной механики не имеют единственного решения в связи с различными гипотезами, принятыми на стадии пластического деформирования. Применительно к геотехническим объектам существуют два направления постановки и решения задач строгой теории:
–упругопластические задачи на основе теории пластического течения (смешанные задачи теорий упругости и пластичности);
–физически нелинейные задачи на основе деформационной теории пла-
стичности грунтов.
Упругопластическая модель (смешанная задача теории упругости и пластичности) грунта основывается на следующих представлениях:
–присущими грунтам являются три вида физической нелинейности: пластическое формоизменение при сложном напряженном состоянии; беспрепятственное деформирование при растяжении; сдвиг по заданной или определяемой расчётом поверхности;
–элемент (элементарный объём) грунта при соответствующем нагружении проходит стадии допредельного и предельного (пластического) напряженных состояний, определяемых физическими уравнениями теорий упругости и пластичности;
–в связи с неравномерным распределением напряжений в грунтовом массиве имеют место оба вида (допредельное и предельное) напряженного состояния, локализирующиеся в областях с фиксируемыми расчетом границами;
–предельные состояния (потеря устойчивости, прогрессирование перемещений) являются следствием развития пластических областей, линий скольжения и накопления присущих им деформаций.
Вернёмся к рис. 21, на котором рассматриваемая модель грунта изображена линией 3. Постановка смешанной задачи теорий упругости и пластичности предполагает совместное использование физических уравнений, формирующих расчётные модели грунта как линейно деформируемой и жёсткопла-
стической сред. Это позволяет использовать в качестве исходных данных те же механические характеристики грунтов (Е, ν, φ, с), которые применяются раздельно в моделях, изображаемых линиями 1 и 2. Физическое содержание указанных характеристик доступно для понимания широкого круга специалистов. Они могут быть определены по стандартным методикам, освоенным в современных грунтовых лабораториях, либо при помощи широко апробированных
табличных данных.
Деформационная теория пластичности грунтов (теория малых упругопластических деформаций А.А. Ильюшина) основана на предположении о том, что объёмная деформация εν =J1 (в соответствии с (1.27) и (1.31)) и интенсивность угловой (формоизменяющей) деформации γ i (в соответствии с (1.29))
44

связаны со средним нормальным напряжением σm и интенсивностью касательных напряжений τi = 
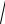 I2 соотношениями
I2 соотношениями
|
|
εν = |
σm |
|
, |
γ i = |
τi |
|
|
, |
(1.41) |
||
|
|
K(σ |
m |
) |
G(τ |
i |
) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
где K(σ m ) = |
σ m |
= tgα и G(τi )= |
τi |
= tgβ |
– переменные секущие |
модули |
|||||||
|
εν |
γ i |
|
|
|
|
|
|
|
|
|
||
объёмной деформации и сдвига, зависящие от σm и τi (рис. 23 а ,б).
а) |
б) |
Рис. 23. Зависимости между инвариантами напряжений и деформаций εν = f1 (σ m ) и γ i = f2 (τi ) в соответствии с деформационной теорией пластичности
Из соотношений (1.41) следуют уравнения связи между напряжениями и деформациями:
εx
εy
εz
=σ x −σ m
2G(τi )
=σ y − σ m
2G(τ i )
=σ z − σ m
2G(τi )
|
|
|
σ |
|
|
|
|
|
+ |
|
|
m |
; |
||||
3K(σ m ) |
||||||||
+ |
|
σ m |
|
|
|
|
; |
|
|
3K(σ |
m |
) |
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
+ |
|
m |
; |
|||||
|
3K(σ m ) |
|||||||
γ xy = Gτ(τxyi );
γ |
|
= |
τ yz |
|
; |
(1.42) |
|
yz |
G(τ i ) |
||||||
|
|
|
|
||||
|
|
|
|
|
|||
γ zx = Gτ(τzxi ).
Криволинейные диаграммы на рис. 23 предполагают единый закон деформирования во всём диапазоне действующих нагрузок. Деление деформаций на упругие и пластические составляющие отсутствует. Это положение затрудняет интерпретацию результатов нелинейного расчёта.
45
Переменные модули K(σ m ) и G(τi ) не являются стандартными показателями механических свойств грунтов. Для их определения нужны специальные лабораторные эксперименты, проводимые без ГОСТов и документов технического регулирования. Геологические лаборатории проектных организаций не оснащены необходимыми приборами.
По указанным выше причинам практическое использование деформационной теории крайне ограничено. Упругопластическая модель с пределами текучести по уравнениям Мора-Кулона и Мизеса-Шлейхера-Боткина остаётся единственной, пригодной для массового проектирования. Только она рассмат-
ривается при дальнейшем изложении.
О геометрической нелинейности. Применительно к геотехническим объектам возможны три случая геометрической нелинейности, под которыми понимается отказ от использования соотношений Коши (1.22).
1.Развитие деформаций в слабых грунтах, когда теряет силу предположение о малости расчётных перемещений. В этом случае изменение местоположения точек при деформировании расчётной области может влиять на распределение усилий в системе.
2.Изгиб тонкостенных конструкций в грунтово-стержневых системах, влияющий на распределение усилий в стенках конструкций и связанные с этим условия деформирования окружающего грунта. Примерами таких конструкций являются трубы из гофрированного металла в дорожных насыпях; ограждения котлованов, устраиваемых вблизи существующих зданий; изгибаемые фундаментные плиты, связанные общими перемещениями с надфундаментными частями зданий.
3.Продольный изгиб центрально и внецентренно сжатых свай, стенок в грунте при поперечных перемещениях осей конструкций.
Контрольные вопросы для самопроверки
1.Опишите физические характеристики грунтов (плотность, пористость, влажность): определения, формульные зависимости, размерности.
2.Назовите классы, виды, разновидности грунтов и определяющие их показатели.
3.Охарактеризуйте пространственное напряжённое состояние, плоскую деформацию, осесимметричную задачу.
4.Изобразите положительные направления осей при решении задач теории упругости и пластичности: координат, усилий, напряжений.
3.Запишите закон Кулона и представьте его графическую форму.
4.Опишите и дайте объяснение метода лабораторного определения грунтов срезу.
5.Опишите и дайте объяснение испытания грунта методом трёхосного сжатия.
46
6.Дайте объяснение и приведите доказательство условия предельного напряжённого состояния грунта по Мору-Кулону.
7.Объясните разницу между предельным равновесием грунта по закону Кулона и предельным напряжённым состоянием по уравнению Мора-Кулона.
8.Приведите записи инвариантов пространственного напряжённого состояния.
9.Что представляют собой фазы напряжённого состояния грунтовых оснований и геотехнических объектов?
10.Охарактеризуйте теории линейного деформирования и жёсткопластичности и области их практического использования.
11.Охарактеризуйте связь видов предельных состояний, расчётных моделей грунта и расчётных проверок сводов правил (СНиП).
47
2.МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
ВМЕХАНИКЕ ГРУНТОВ
Современная прикладная (применяемая в проектной практике) нелинейная механика грунтов использует в качестве своей математической основы метод конечных элементов (МКЭ). Изучению этого метода как средства решения нелинейных задач должно предшествовать знакомство с его теоретической и линейной основой. Настоящий раздел содержит изложение и обоснование уравнений и математических процедур МКЭ в объёме, необходимом для последующего восприятия идей, алгоритмов и прикладных задач нелинейной механики грунтов.
2.1. Теоретические основы МКЭ. Идеи, постулаты
Общие положения. МКЭ позволяет на единой вычислительной основе осуществить расчёт систем любой конфигурации (плоских, осесимметричных, пространственных, комбинированных), встречающейся в строительном и геотехническом проектировании, с произвольным нагружением. Расчётная схема проектируемого (или исследуемого) объекта условно делится на конечные элементы (КЭ) с конечным числом степеней свободы, понимаемых как определяемые в расчёте векторы перемещений узлов. На рис. 24 приводятся примеры такого деления. Контактирующие КЭ, представляющие собой топологически изученные геометрические фигуры, сопрягаются (скрепляются) общими узлами (вершинами, рёбрами).
Каждому узлу и каждому КЭ присваивается порядковый номер. Обе нумерации начинаются с 1. Расчётная область находится под действием сил и моментов, приложенных в узлах (узловых сил). Температурные воздействия и нагрузки, приложенные к точкам и площадкам внутри КЭ, заменяются эквивалентными наборами узловых сил.
На рис. 24 и 25 представлены наиболее употребительные в современном проектировании разновидности КЭ с указанием векторов степеней свободы узлов.
В стержневых плоских (пространственных) КЭ возможны три (шесть) степени свободы: две (три) осевые x1, z1 (x1, y1, z1) по направлениям в системе координат на рис. 24 и одна угловая (поворот) относительно оси y1 (три угловые относительно осей x1, y1, z1). Напряжённое состояние плоских (пространственных) стержней, определяемое по результатам расчёта, описывается продольной силой в направлении оси x1, поперечной силой в направлении оси z1 (поперечными силами в направлении осей y1, z1), изгибающим моментом относительно оси y1 (изгибающими моментами относительно осей y1, z1 и крутящим моментом относительно оси x1).
48
