
Учебники 80377
.pdf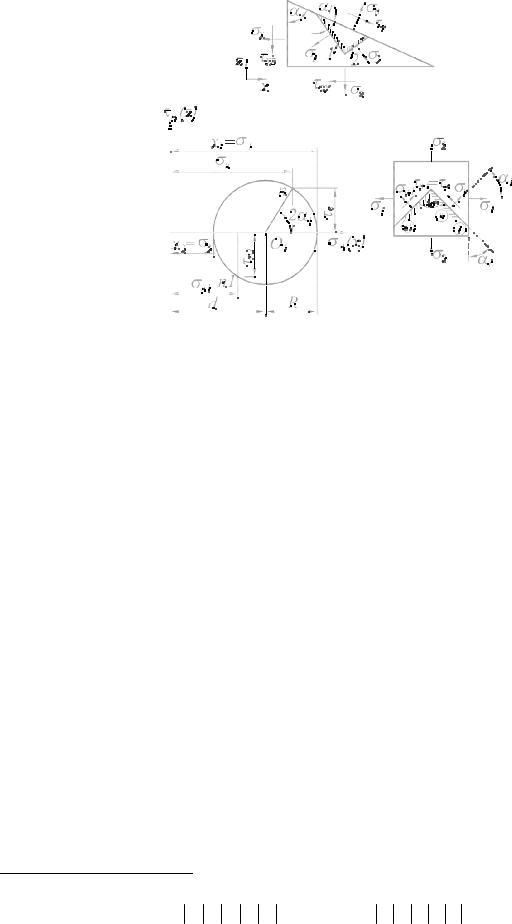
а)
б)
Рис. 10. Схемы к описанию напряженного состояния в точке:
а – к уравнениям (1.4) и (1.6); б – круг Мора и взаимное положение площадок 1, п и п1
Объединение уравн ений (1.3) и (1.6) позволяет получить угол наклона площадок скольжения к главным площадкам 450–φ/2 и запись
σ1 − σ 2 |
+ |
σ1 + σ 2 |
sinϕ − ccosϕ = 0, |
(1.7)1 |
|
|
|||
2 |
2 |
|
|
|
которая известна как усло вие прочности грунта в точке по Мору-Кулону.
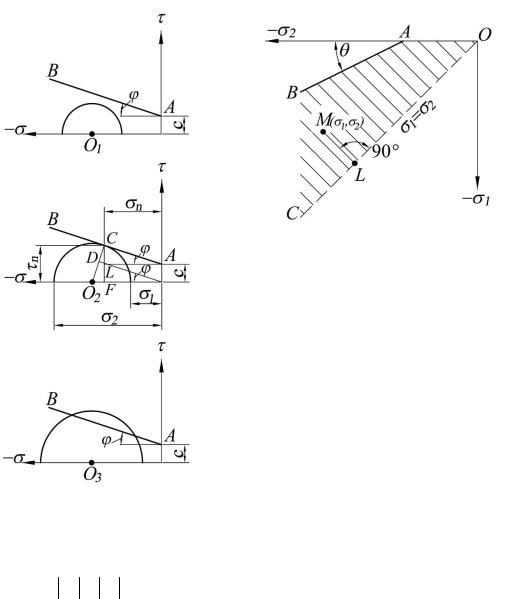
На рис. 11, а, б пр едставлены графические иллюстрации к уравнению (1.7). Прямая АВ, выража ющая зависимость (1.3), совмещена на одном графике с кругами Мора, изображающими три качественно различных напряжённых состояния грунта в точке (см . рис. 11, а). Расположение круга М ора ниже прямой АВ означает, что левая часть уравнения (1.7) меньше нуля и прочность грунта обеспечена. Касание прям ой АВ круга Мора с центром О2 показывает, что на одной из площадок, проходящих через исследуемую точку, имеет место пре-
дельное равновесие в соответствии с зависимостью (1.7). Ур авнение (1.7) может быть получено из пост роений на диаграмме для этого круга: О2С=О2D+DC, где О2С=½(σ1–σ2), О2D=½(σ1+σ2) sinφ, DC=c cosφ. Из рассмат риваемого рисун-
ка (круг Мора с центром О2) также видно, что вектор О2С образует с осями главных напряжений σ1,2 у глы π/2 φ, что соответствует углам наклона площадок скольжения к главным площадкам 450 φ/2.
Согласно излагаемой теории круг Мора не должен пересекать прямую, выражающую закон Куло на, так как грунт не может воспринять изображаемое
1 Напомним, что сжатие счи тается отрицательным направлением напряжений и деформаций: σ 3 ≤ σ 2 ≤ σ 1 , σ3 ≥ σ2 ≥ σ1 ; ε3 ≤ ε 2 ≤ ε1 , ε3 ≥ ε2 ≥ ε1 .
19
напряжённое состояние. Если по результатам расчёта такое положение (круг с центром О3) всё же получено, то это свидетельствует о несовершенстве метода определения компонентов напряжений в грунтовом массиве.
а) |
б) |
Рис. 11. Графические иллюстрации к условию прочности Мора-Кулона (а) и области COAB физически возможных напряженных состояний на плоскости σ1, σ 2 (б)
На рис. 11, б изображена плоскость главных напряжений σ1,2 . Ось симметрии ОС соответствует гидростатическому напряжённому состоянию σ1=σ2. Так как σ1≥σ2 ( σ2 ≥ σ1 ), действительной является только часть диаграммы выше оси ОС. Если напряжённое состояние в элементарном объёме грунта изо-
бражается точкой М с координатами σ1, σ2, |
то точка L |
соответствует |
|||||
σср = σ1 + σ2 , а проекции отрезка LM на оси координат равны τ max |
= |
σ1 −σ 2 |
. |
||||
|
|||||||
2 |
|
|
|
|
2 |
|
|
Прямая АВ, наклонённая к оси σ2 под углом θ = |
|
2 |
ϕ |
|
|
|
|
arctg tg |
45 − |
|
|
и пересе- |
|||
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
ϕ |
|
2c cosϕ |
|
|
кающая её на расстоянии σ 2 |
= OA = −2c ctg 45 |
− |
|
= − |
|
от начала ко- |
|
1− sinϕ |
|||||||
|
|
|
2 |
|
|
ординат, является графической формой уравнения (1.7). Поэтому для грунта
20

физически возможными считаются только такие координаты σ1, σ2, при которых изображаемая точка находится в области ОАВС.
В учебной и научно-технической литературе встречаются записи условия прочности грунта в точке, тождественные уравнению (1.7), полученные в результате его преобразований. Приведём два из таких выражений:
|
σ 2 |
|
+ σ с |
|
σ с − σ 2 |
|
|
2 |
|
ϕ |
|
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
= ctg |
|
45° − |
, |
(1.8) |
|
|
σ1 |
|
|
+ σ с |
|
σ с − σ1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
σ1 −σ 2 |
|
= sinϕ , |
|
(1.9) |
||||||
|
|
|
|
|
σ1 |
|
|
+ |
|
σ 2 |
|
+ 2σ с |
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
c
где σc = tgϕ – характеристика грунта, называемая «давлением связности».
Условие прочности по Мору-Кулону широко и успешно применяется в научных исследованиях и инженерной практике. В настоящее время в теории механики грунтов нет другого равноценного постулата для условий плоской задачи, сочетающего простоту, ясность физического смысла и удовлетворительное соответствие данным наблюдений и научных ис-
следований.
Пространственная задача. Перейдём к рассмотрению условий прочности при пространственном (трёхмерном) напряжённом состоянии, определяемом главными напряжениями σ1, σ2, σ3 (или σ1,2,3) и изображаемом графически в виде точки М на рис. 12, а. При анализе трёхмерно-
го напряжённого состояния используются следующие приёмы.
1. Разложение тензора напряжений на гидростатическую (шаровой тензор) и девиаторную части. Под тензором напряжений в точке пони-
мается совокупность напряжений, действующих на трёх взаимно перпендикулярных площадках (рис. 12, б). Матричная запись тензора напряжений имеет вид:
|
σ x |
τ xy |
τ xz |
|
σ1 |
0 |
0 |
|
|
|
|
|
|
||||||
Tσ = |
τ yx |
σ y |
τ yz |
или |
0 |
σ 2 |
0 |
. |
(1.10) |
|
τ zx |
τ zy |
σ z |
|
0 |
0 |
σ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
Гидростатическая часть напряжённого состояния включает три пары равных напряжений:
21
σm = |
σ x +σ y +σ z |
= |
σ |
1 |
+σ |
2 |
+σ |
3 |
. |
(1.11) |
|
3 |
|
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
Напряжения σm не меняют своей величины при по вороте осей, т. е. являются равными (и одновременно главными) на всех пл ощадках, проходящих через точку М.
Матричная запись шарового тензора имеет вид:
|
σ m |
0 |
0 |
|
|
|
|
|
|||
Tш = |
0 |
σ m |
0 |
. |
(1.12) |
|
0 |
0 |
σ m |
|
|
а) |
б) |
в)
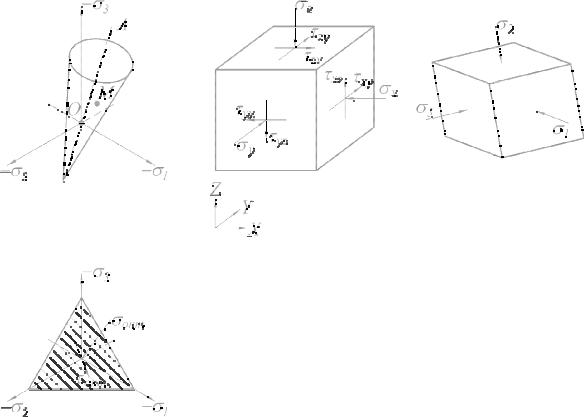
Рис. 12. Пространство главных напряже ний σ1 , σ 2 , σ 3 и графическая форма условия прочности Мизеса-
Шлейхера-Боткина (а); компоненты нап ряжений в условиях пространственной задачи (б); октаэдрическая площадка (в)
Девиаторная часть в ключает касательные напряжения и разности между нормальными напряжения ми и их средним значением σ m . Матричная запись девиатора напряжений им еет вид:
22
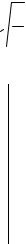
|
σ x −σ m |
τ xy |
τ xz |
|
|
|
|
|
|||
Dσ = |
τ yx |
σ y −σ m |
τ yz |
. |
(1.13) |
|
τ zx |
τ zy |
σ z −σ m |
|
|
Девиаторное напряжённое состояние характерно тем, что его сумма главных напряжений равна нулю.
Матрицы (1.10), (1.12), (1.13) связаны равенством
Tσ = Tш + Dσ . |
(1.14) |
Шаровой тензор вызывает изменение объёма, девиатор – формоизмене-
ние.
2. Использование инвариантов напряжённого состояния, т. е. таких комбинаций напряжений, которые не меняют своих значений при повороте осей. Наибольшее практическое значение имеют первый инвариант тензора напряжений
|
|
|
|
|
|
|
|
|
I1 |
= σ x |
+ σ y |
+ σ z |
|
= σ1 + σ 2 + σ 3 |
|
|
|
(1.15) |
|||||||||||||||||||||
и второй инвариант девиатора напряжений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
I |
|
= |
1 |
[(σ |
|
− σ |
|
)2 |
|
+ (σ |
|
−σ |
|
)2 + (σ |
|
− σ |
|
)2 ]= |
|
|
|||||||||||||||
|
|
|
|
2 |
|
1 |
2 |
|
2 |
3 |
1 |
3 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
[(σ |
|
− σ |
|
)2 + (σ |
|
− σ |
|
)2 + (σ |
|
− σ |
|
)2 |
+ 6(τ 2 |
+τ 2 |
+τ 2 |
)]= |
|||||||||||||||||||||
|
x |
y |
y |
z |
z |
x |
|||||||||||||||||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
yz |
zx |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
= |
1 |
[σ |
2 |
+ σ |
|
2 |
+ σ |
2 |
− (σ σ |
|
|
+ σ |
σ |
|
|
+ σ σ |
|
)] |
. |
(1.16) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
1 |
|
2 |
|
|
2 |
|
|
3 |
3 |
|
1 |
|
|
|
||||
Ось симметрии ОА на рис. 12, а изображает гидростатические напряжённые состояния σ1=σ2=σ3. Эта прямая наклонена к осям σ1,2,3 под равными угла-
ми arcsin 2 и является нормалью к девиаторной плоскости, проходящей через  3
3
начало координат и определяемой тем, что суммы координат её точек σ1+σ2+σ3.
Покажем способ получения инвариантов I1, I2 и доказательство их независимости от положения осей координат. Выполним для этого следующие построения. В параллелепипеде на рис. 13 выделим тетраэдр, образованный наклонной плоскостью, пересекающей оси координат Х, Y, Z. Предположим, что выбранная (обозначенная штриховкой) наклонная плоскость является одной из трёх главных площадок в рассматриваемой точке, и нормаль v параллельна σ – одному из трёх главных напряжений.
23
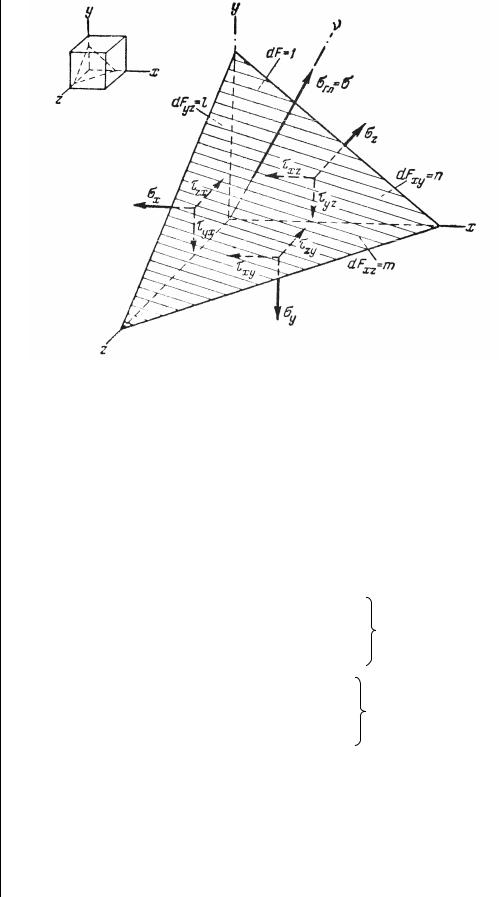
Рис. 13. Схема к уравнениям (1.13)
Обозначим через l, m, n направляющие косинусы нормали v по отношению к осям Х, Y, Z. Направляющие косинусы связаны соот-
ношением
l2+m2+n2=1. (a)
Отношения площадей граней, лежащих на координатных плоскостях, к площади Fv главной площадки, нормальной к оси v, будут равны Fyz/Fv=l, Fxz/Fv=m, Fxy/Fv=n. Запишем три уравнения равновесия проекций напряжений на оси Х, Y, Z:
Fv [(σx–σ)l+τxym+τxzn]=0;
Fv [τyxl+(σy–σ)m+τyzn]=0; (б) Fv [τzxl+τzym+(σz–σ)n]=0
или
(σx–σ)l+τxym+τxzn=0;
τyxl+(σy–σ)m+τyzn=0; (1.17) τzxl+τzym+(σz–σ)n=0.
В высшей алгебре системы уравнений этого вида называются однородными с двумя вариантами решения относительно неизвестных, которыми в нашем случае являются направляющие косинусы l, m, n. Первый вариант – l, m, n равны нулю. Это невозможно, так как противоречит уравнению (a). Второй вариант – определитель системы (1.17) равен нулю:
24

|
σ x − σ |
τ xy |
τ xz |
|
|
∆ = |
τ yx |
σ y − σ |
τ yz |
= 0 |
(в) |
|
τ zx |
τ zy |
σ z − σ |
|
|
Раскрытие определителя (в) ведёт к кубическому уравнению следующего вида:
σ3 – I1σ2 – I2σ – I3=0. |
(1.18) |
Три корня уравнения (1.18) являются значениями трёх главных напряжений σ1, σ2, σ3. Коэффициенты уравнения (1.18) являются инвариантами тензора напряжений:
I1=σx+σy+σz,
I2=–σx σy – σy σz – σzσx + τxy2 + τyz2 + τzx2, (1.19)
I3=σxσyσx – σx τyz2 – σy τxz2– σz τxy2+2τxy τyz τxz.
Инвариантность выражений (1.19) обосновывается тем, что при одних и тех же значениях главных напряжений σ1, σ2, σ3 коэффициенты I1, I2, I3 не зависят от положения координатных осей.
Решение системы (1.17) можно получить путём подстановки вместо σ одного из трёх σ1,2,3 главных напряжений, полученных в
результате решения кубического уравнения (1.18), совместно с уравнением (а).
Получим теперь инвариант I2 для условий девиатора напряжений в соответствии с (1.13). Для этого в запись этого инварианта в составе (1.19) вместо σx,y,z введём выражения (σx,y,z–⅓I1), а последние три члена τxy2+τyz2+τzx2 оставим без изменения и временно исключим из рассмотрения. Выполним тождественные преобразования с первыми тремя членами:
–(σx–⅓I1)(σy–⅓I1) –(σy–⅓I1)(σz–⅓I1)–(σz–⅓I1)(σx–⅓I1)= =–[σxσy–⅓I1(σx+σy)+(⅓I1)2]–[σyσz–⅓I1(σy+σz)+(⅓I1)2]–
–[σzσx–I1(σz+σx)+(⅓I1)2]=
=–σx σy – σy σz – σzσx+⅔I12–⅓I12=–σx σy – σy σz – σzσx+⅓I12= =–σx σy – σy σz – σzσx+⅓(σx2+σy2+σx2+2σx σy+2σy σz+2σzσx)= =⅓(σx2+σy2+σx2–σx σy – σy σz – σzσx)= 16 [(σx–σy)2+(σx–σy)2+(σx–σy)2].
Присоединяя к последнему выражению τxy2+τyz2+τzx2, получаем окончательный вид второго инварианта девиатора напряжений в соответствии с (1.16):
I2= 16 [(σx–σy)2+(σx–σy)2+(σx–σy)2]+τxy2+τyz2+τzx2=
= 16 [(σx–σy)2+(σx–σy)2+(σx–σy)2+6τxy2+6τyz2+6τzx2].
25

В механике грунтов при анализе пространственного напряжённого состояния используется условие прочности Мизеса-Шлейхера-Боткина, описываемое уравнением
I2 |
+ aI1 − k = 0, |
(1.20) |
где α и k – прочностные характеристики грунта, подобные sinϕ и с в уравнении (1.7).
Графической формой уравнения (1.20) является коническая поверхность, ось которой совпадает с гидростатической (рис.12, а). Физически возможными являются напряжённые состояния {σ 1σ 2σ 3 }, изображённые на рис.12, а точками М, находящимися на конической поверхности (1.20) или внутри неё.
Уравнение (1.20) тождественно соотношению с более конкретным физическим содержанием, выражающему предельное равновесие на октаэдрической площадке, аналогичное закону Кулона:
τ окт = |
|
σ окт |
|
tgρокт + nокт , |
(1.21) |
|
|
где τ |
|
= |
|
2 |
I |
|
, σ |
|
= |
I1 |
– касательное и нормальное напряжения на октаэд- |
окт |
|
|
2 |
окт |
|
||||||
|
|
|
3 |
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|||
рической (равнонаклонённой с осям главных напряжений, рис.12, в) площадке; ρокт и покт – прочностные характеристики грунта. Уравнения (1.20) и (1.21) то-
ждественны при α = |
tgρокт |
и k = |
|
3 |
|
n |
окт |
. |
||
|
|
|
2 |
|||||||
|
||||||||||
6 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
Уравнение (1.7) и тем более (1.20), (1.21) изменяют первоначальное представление о механизме разрушения грунта. Если по закону Кулона это явление происходит как взаимное смещение частей сыпучего тела, то условия прочности Мора-Кулона и Мизеса-Шлейхера-Боткина объясняют разрушение как результат формоизменяющего (девиаторного) воздействия приложенных сил.
Испытание грунта методом трёхосного сжатия. Физической иллюстрацией формы разрушения в соответствии уравнениями (1.7) и (1.20) является лабораторное испытание образцов грунта цилиндрической формы в соответствии с ГОСТ 12248-2010 в приборе трёхосного сжатия (стабилометре) с принципиальной схемой на рис. 14. Прибор допускает деформации образца грунта в радиальном направлении при фиксированном (контролируемом) горизонтальном давлении. Размеры образца: диаметр не менее 35 мм, отношение высоты к диаметру от 1,85:1 до 2,25:1.
Опыт заключается в приложении к образцу грунта (ненарушенного сложения с природной влажностью или нарушенного сложения с заданными значениями плотности и влажности) осесимметричной системы сил (рис. 15, а): вертикальных σ3 и горизонтальных
26
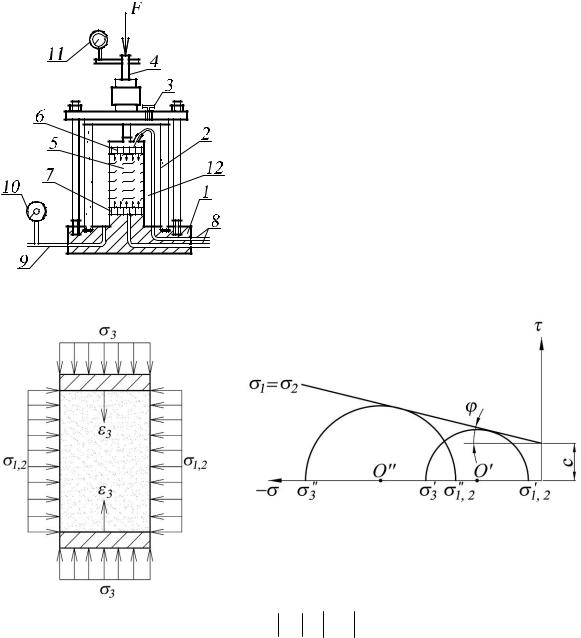
Рис. 14. Принципиальная схема прибора для испытания грунта методом трехосного сжатия:
1 – основание камеры; 2 – корпус камеры; 3 – вентиль для выпуска воздуха; 4 – шток; 5 – образец грунта в оболочке; 6 – верхний штамп; 7 – нижний штамп; 8 – трубки для дренирования и измерения порового давления; 9 – трубка для заполнения камеры и измерения давления в камере; 10 – манометр; 11 – индикатор; 12 – жидкость
а) |
б) |
Рис. 15. К анализу результатов испытания грунта методом трехосного сжатия: а – схема приложения напряжений σ3 и σ1,2 к образцу грунта; б – определение ϕ и с
(радиальных) напряжений σ1 =σ2 (σ3 > σ1,2 ). При каждом отдельном испыта-
нии радиальные напряжения σ1,2 остаются постоянными, а напряжения σ3 увеличиваются небольшими ступенями. Испытание считается законченным после исчерпания прочности грунта по одному из следующих признаков: разрушение образца; пластическое течение без приращения напряжений σ3; достижение относительной деформацией величины ε3 = − 0,15. Опыт повторятся не менее трёх раз (с тремя образцами исследуемого грунта) при разных значениях радиальных напряжений σ1,2. По результатам измерений по известным значениям пар главных напряжений (σ΄1,2, σ΄3; σ˝1.2, σ˝3; σ˝΄1.2, σ˝΄3) определяются значения прочностных характеристик (φ и с или α и k) расчётным путём в соответствии с уравнениями (1.7) или (1.20) или графически при помощи диаграмм на рис. 15,б.
27

ГОСТ 12248-2010 предусматривает три варианта проведения опыта:
–неконсолидированное-недренированное испытание – для опре-деления сопротивления сдвигу водонасыщенных глинистых, органо-минеральных и органических грунтов природной плотности;
–консолидированное-недренированное испытание с измерением порового давления – для определения характеристик прочности φ и с для водонасыщенных в природных условиях дисперсных грунтов;
–консолидированное-дренированное испытание – для определения характеристик прочности φ, с и характеристик деформируемости Е, ν дисперсных грунтов.
1.4. Зависимости между перемещениями, напряжениями и деформациями
В настоящем параграфе рассматриваются условия деформирования грунтов (связи между перемещениями, напряжениями и относительными деформациями) с делением на стадии линейного деформирования и пластического течения (до и после достижения условия текучести в соответствии с уравнения-
ми Мора-Кулона или Мизеса-Шлейхера-Боткина).
Соотношения Коши и обобщённый закон Гука. Напомним обозначения составляющих перемещений в точке U, W, V по направлениям осей X, Y, Z
ивведём обозначения деформаций: εx, εy, εz, γxy, γxz, γyz – относительные осевые
иугловые деформации в прямоугольных координатах; ε1, ε2, ε3 – главные относительные деформации.
Линейные соотношения, связывающие перемещения, относительные деформации и напряжения, имеют следующий вид.
Соотношения Коши связи между перемещениями и деформациями (выражают непрерывность и относительную малость перемещений):
|
|
|
ε x |
= ∂U |
, |
ε y = |
∂W |
, ε z = |
∂V |
, |
|
|
|
|
||||||||
|
|
|
|
|
|
∂z |
|
|
|
|
||||||||||||
|
|
|
|
|
∂x |
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
||||
γ |
|
= |
∂U |
+ |
∂W |
, γ |
|
= |
∂W |
+ |
∂V |
, γ |
|
= |
∂U |
+ |
∂V |
. |
(1.22) |
|||
xy |
∂y |
|
yz |
∂z |
|
xz |
||||||||||||||||
|
|
∂y |
|
|
||||||||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
∂z |
|
∂x |
|
|||||||||
Напомним читателям происхождение указанных выше уравнений. С этой целью рассмотрим проекцию и перемещения на плоскости XOZ элементарного объёма упругого тела с размерами dx dy dz (рис. 16). В соответствии с изображением на рисунке абсолютные удлинения по направлениям X и Z соответственно равны (дU/дх)dx и (дV/дy)dy, а относительные удлинения (деформации)
28
