Учебное пособие 800396

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

li xi2 yi2

li xi2 yi2

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

2.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

□ Имеем

	b		b				b		b
						dx udv vdu,
	uv dx u v uv					dx udv vdu,
	a		a				a		a
но, согласно формуле Ньютона – Лейбница,
			b
			uv dx uv				ba ,


			a
откуда сразу следует доказательство теоремы.									■
		2
Пример. Найти ln xdx.
		1
Решение:
2				1					2
ln xdx u ln x;			du x		dx x ln x			12	dx 2ln 2 1.
ln xdx u ln x;			du x		dx x ln x			12	dx 2ln 2 1.
1	dv dx;		v x						1

23.ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

23.1. Вычисление площадей в прямоугольных координатах с помощью определенного интеграла

Т.к.	lim	b	f x dx,	то это означает, что, если f x 0	,
Т.к.	0			то это означает, что, если f x 0	,
		a
		a

определенный интеграл равен площади криволинейной трапеции, ограниченной кривой y f x , осью Ох и прямыми x=a и x=b, т.е.

S f x dx.

Если f x 0 на a,b , то и S 0, и поэтому, если f x конечное число раз меняет знак на a,b , то площадь под (над) кривой y f x необходимо находить по формуле (рис. 5)

S f x dx.

Рис. 5

Пример. Вычислить площадь фигуры, ограниченной синусоидой

y sin x и осью Ох, при 0 x 2 .
Решение. Т.к. sin x 0	при 0 x , и sin x 0				при x 2
(рис. 6), то
	2				2
	S		sin x	dx sin xdx	sin xdx


	0	0

cos x 0 cos x 2 cos cos0

cos 2 cos 1 1 1 1 4.

Рис. 6

23.2. Вычисление площади с помощью определенного интеграла при задании функции в параметрической форме

Пусть y f x задана в параметрической форме:

		x t ,	y t ,
где t ,	a,	b.
	b	x t
	S f x dx		t t dt.
	a	dx	t dt

Пример. Вычислить площадь области, ограниченной эллипсом x a cost, y bsin t.

Решение. Вычислим площадь верхней половины эллипса и удво-

им. Здесь x a, a					t ,0 .
	0				0				cos 2t
S 2 bsin t a sin t dt 2ab sin2tdt 2ab sin2tdt 2ab								1	cos 2t	dt
S 2 bsin t a sin t dt 2ab sin2tdt 2ab sin2tdt 2ab									2	dt
						0	0		2
						0	0
	t		sin 2t
	t		sin 2t
2ab				ab.
2ab				ab.
		2	4	0
				0

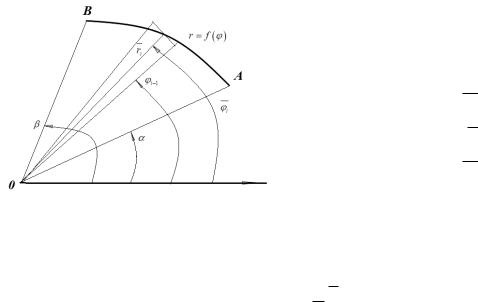
23.3.Вычисление площади криволинейного сектора в полярных координатах с помощью определенного интеграла

Пусть в полярной системе координат задана кривая r f , где f непрерывная на , (рис. 7).

Выберем

i ii 0n .

Пусть

i 1 i i .

Обозначим через ri радиус-вектор, соответствующий i .

Рис. 7

Площадь кругового сектора

Si 12 ri 2 i .

Составим Риманову сумму

1	n			1	n		i .
			2 i		f 2
		ri				i

2 i 1				2 i 1

В силу непрерывности f

lim		1	r2d .
lim			r2d .
0	2
	2

	83

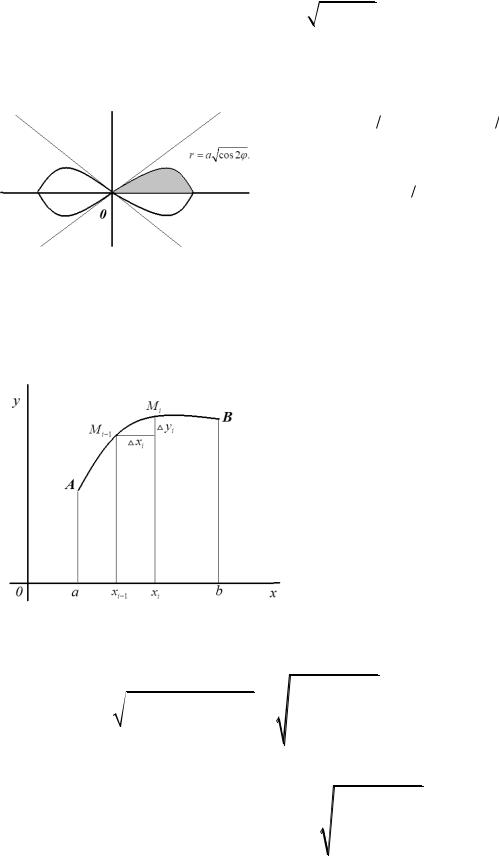
Пример. Вычислить площадь фигуры, ограниченной лемниска-

той

r a 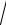cos 2 .

Решение. Радиус-вектор опишет область с площадью, равной

четверти искомой площади (рис. 8), если 0								.
								4
	1				1	4			1		4
	1	S			1	r2d			1	a2	cos 2 d
		S				r2d				a2	cos 2 d
4					2	0		2			0
						0					0
			a2	sin 2			4	a2
							4
												S a2 .
		2				2		4				S a2 .
		2				2	0	4
Рис. 8							0
Рис. 8
23.4. Длина дуги кривой в прямоугольных координатах
					Пусть дана y f x ,								x a,b

(рис. 9).

Выберем

xi ii 0n .

Длину кривой АВ приближенно представим, как

LAB Mi 1M i , i 1

Рис. 9

но Mi 1Mi 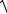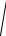xi 2 yi 2

В силу непрерывности

1 yi

f x

xi .

		n
lim lim
0	n	i 1
		i 1

1 yixi

xi .

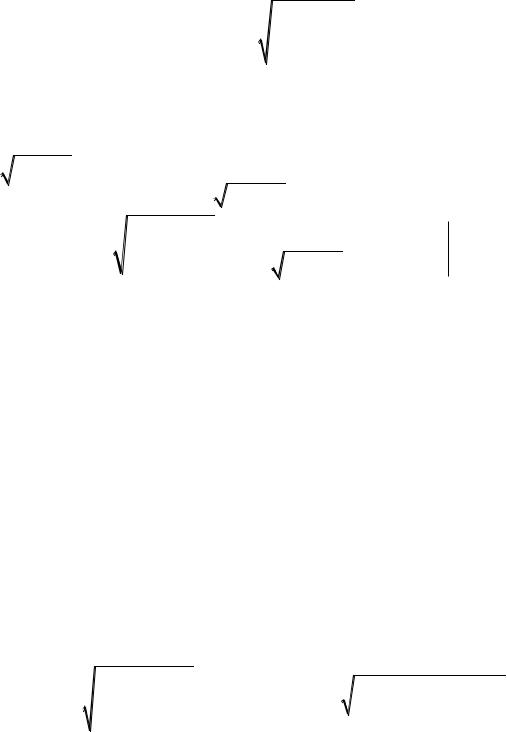
По теореме Лагранжа имеем
	yi		f xi f xi 1	f i ,		где i xi 1, xi ,
	xi		xi xi 1	f i ,		где i xi 1, xi ,
	xi		xi xi 1
причем при xi		0 i x, тогда

			b		dy	2
			LAB		dy
				1		dx.
				1		dx.
			a		dx
			a
Пример. Определить длину окружности x2 y2 r2 .

Решение. Вычислим вначале длину четверти окружности, лежащей в I-м квадранте. Тогда уравнение ее будет

r2 x2 , откуда

r2 x2

rdx

r arcsin

r2 x2

тогда l 2 r.

r 2 ,

23.5. Длина кривой в параметрической форме

Пусть y f x в виде

x t ,

y t ,

t ,

где t , t непрерывные

функции

с непрерывными

производ-

ными, t 0,тогда

Пусть

a ,

и сделаем

подстановку

x t ,

dx t dt, тогда

t dt

или l

dt.

Пример. Вычислить длину астроиды

x a cos3 t,

y asin3 t.

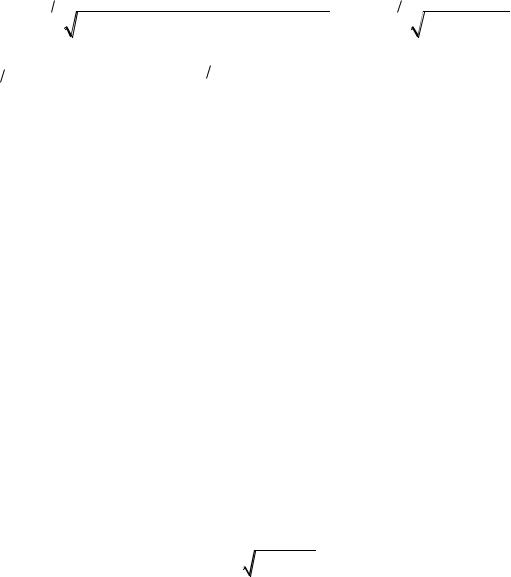
Решение. Т.к. кривая симметрична относительно обеих координатных осей, то вычислим сначала длину ее четвертой части, расположенной в I-м квадранте. Находим

					dx	3a cos2 t sin t;					dy	3a sin2 t cost.
						3a cos2 t sin t;						3a sin2 t cost.
					dt						dt
Параметр t будет изменяться от 0 до
											2
	1		2										2
	1	l		9a2 cos4 t sin 2t 9a2 sin4 t cos 2t dt 3a										cos2 t sin2 t dt
4		l		9a2 cos4 t sin 2t 9a2 sin4 t cos 2t dt 3a										cos2 t sin2 t dt
4			0										0
			0										0
2							sin2 t	2	3a
								2

3a sin t cost dt 3a										;	l 6a.
3a sin t cost dt 3a										;	l 6a.
0				2				0	2
0								0

23.6. Длина дуги кривой в полярных координатах

Пусть в полярных координатах задано уравнение кривой

r f .

Воспользуемся

формулами

перехода

от

полярных координат

к декартовым:

x r cos ,

y r sin ,

или x f cos ,

y f sin .

Найдем

cos f sin ,

sin f cos ,

d f

тогда

dx 2

dy 2

r 2 r2

r 2 r2 d .

Пример. Найти длину кардиоиды r a 1 cos .

Решение. Изменяя полярный угол от 0

до ,

получим поло-

вину искомой длины. Здесь r asin

				d
l	a2 1 cos 2 a2 sin2 d 2a		d 2a cos
		2 2cos
0	0	0		2

8asin 8a. 2 0

23.7.Вычисление объема тела по площадям параллельных сечений

Пусть имеется некоторое тело Т. Предположим, что известна площадь любого сечения этого тела плоскостью, перпендикулярной к оси Ox (рис. 10). Эта площадь будет зависеть от положения секущей плоскости, т.е. будет функцией х:

		S S x .
		Предположим, что	S x	есть
		непрерывная функция от х.
		Проведем плоскости
		x x0 a; x x1; x x2 ;...x = xn		b.
		Эти плоскости разобьют тело
		на слои.
		Т.о., имеем x i n , тогда
		i	i 0
Рис. 10
объем i-го слоя есть
	n
	Vn S i xi ,
	i 1
где xi 1 i xi ; xi	xi xi 1, а объем всего тела Т будет
	V limV	b S x dx.
	0 n
		a
		a

Пример. Вычислить объем эллипсоида

x2	y2	z2	1.
a2	b2	c2

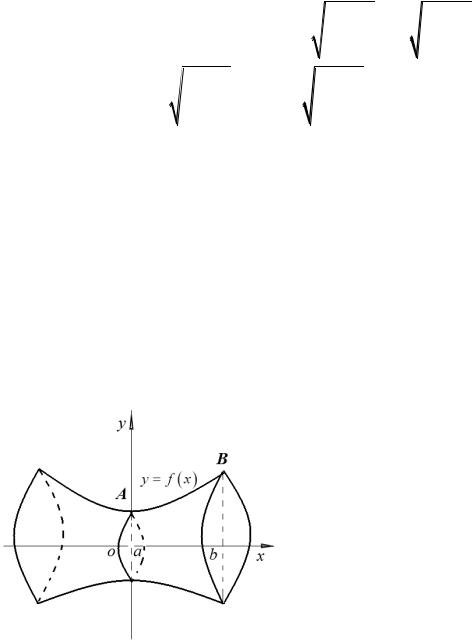
Решение. В сечении эллипсоида плоскостью, параллельной плоскости Oyz и отстоящей на расстоянии х от нее, получится эллипс

;

с полуосями b b

;

c c

Но площадь такого эллипса

равна b1c1, поэтому

S x bc 1

Объем эллипсоида будет равен

V bc

dx bc x

abc.

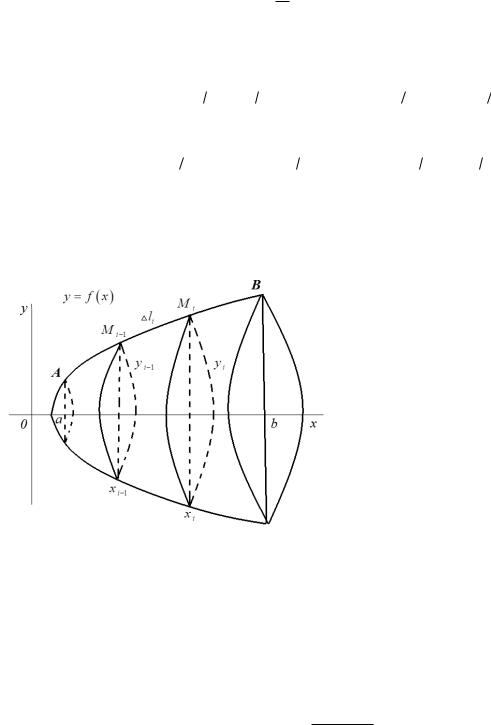
23.8. Объем тела вращения

Рассмотрим тело, образованное вращением вокруг оси Ох криволинейной трапеции aABb, ограниченной кривой y f x , осью Ох и пря-

мыми x a, x b (рис. 11).

В этом случае произвольное сечение тела плоскостью, перпендикулярной к оси Ох, есть круг, площадь которого

S x f x 2 .

Рис. 11

Применим формулу из п. 23.7:

	b
V	f x	2 dx.

	a

Пример. Найти объем тела, образуемого вращением цепной линии

y a2 exa

вокруг оси Ох на участке от 0 до b.

Решение:

					2	b
V				a		ex a e x a 2 dx
V				4		ex a e x a 2 dx
						0
	a2	a					a		b
	a2	a					a		b
					e2 x a 2x			e 2 x a
					e2 x a 2x			e 2 x a
	4		2				2		0
									0

e xa .

	2	b
a		e2 x a 2 e 2 x a		dx
4		e2 x a 2 e 2 x a		dx
		0
	a2		e2b a e 2b a		a2b	.
		8			2

23.9. Площадь поверхности тела вращения
Пусть	дана		поверх-
ность, образованная враще-
нием кривой		y f x ,
вокруг оси Ох. Найдем
площадь этой		поверхности
на a,b (рис. 12).
Пусть	f x и		f x
непрерывны на a,b .
Выберем
x		i n .
	i	i 0

Рис. 12

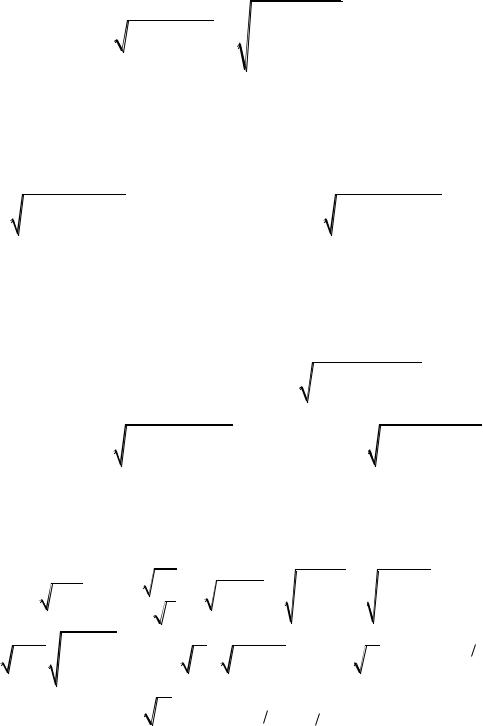
Точки Mi f xi соединим прямыми отрезками, которые обозначим через li . Каждый отрезок при вращении образует усеченный

конус, площадь которого

Si 2 yi 1 yi li , 2

но

Применим теорему Лагранжа

xi 1

f i ,

xi 1

где xi 1

yi 1 yi

l 1

и S

x ,

тогда

Si ,

i 1

но, в силу непрерывности f x

и f x , имеем

f x

2 x

lim

f x

1 f

max x 0

i 1

1 f

2 x

x 1 f x 2 dx.

lim

2 f

max xi 0

i 1

Пример. Определить площадь поверхности параболоида, образо-

ванного вращением вокруг оси Ох дуги параболы y2 2 px,

x 0, a .

Решение:

2 p

2x p

2 px; y

2 x ;

1 y

2x .

2x p

2x p 3 2

S 2

dx 2

2 px

2x p dx 2

2a p 3 2 p3 2 .

23.10. Вычисление работы с помощью определенного интеграла

Пусть под действием силы F материальная точка М движется по прямой Ох, причем направление F совпадает с направлением Ох.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20222.17 Mб3Учебное пособие 800391.pdf
#
01.05.20222.19 Mб2Учебное пособие 800392.pdf
#
01.05.20222.21 Mб6Учебное пособие 800393.pdf
#
01.05.20222.21 Mб5Учебное пособие 800394.pdf
#
01.05.20222.22 Mб19Учебное пособие 800395.pdf
#
01.05.20222.23 Mб6Учебное пособие 800396.pdf
#
01.05.20222.24 Mб5Учебное пособие 800397.pdf
#
01.05.20222.27 Mб10Учебное пособие 800398.pdf
#
01.05.20222.27 Mб7Учебное пособие 800399.pdf
#
01.05.2022158.06 Кб2Учебное пособие 8004.pdf
#
01.05.2022349.85 Кб2Учебное пособие 80040.pdf