
Учебное пособие 800396
.pdf
Пример.
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4x2 2x 1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dx |
|
|
|
|
|
|
|
1 2 |
|
3 |
|
|
|||
Решение: |
|
|
|
|
4x2 |
2x 1 |
4 |
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||||||||||
|
4x2 2x 1 |
|
|
|
|
|
|
|
4 |
|
16 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
t |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
x |
1 |
|
2 |
|
3 |
|
|
|
|
|
1 |
2 |
|
|
|
3 x t |
; dx dt |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
t t 2 |
|
|
|
|
|
|
|
C |
|
|
ln |
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
C. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
t 2 |
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
16 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Интегралы |
|
|
типа |
|
|
|
|
|
|
|
|
|
|
Pn x |
|
|
|
|
dx, |
где |
|
|
P |
x |
многочлен |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax2 bx c |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
степени n, можно вычислить, пользуясь формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Pn x |
|
|
|
|
|
dx Q |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax2 bx c |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ax2 bx c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax2 bx c |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
где |
|
Qn 1 x |
|
|
многочлен |
|
|
|
|
|
|
степени |
|
|
|
|
|
|
n-1 |
|
|
с |
|
|
|
неопределенными |
|||||||||||||||||||||||||||||||||||||||||||||||||
коэффициентами, также неопределенный коэффициент.
Все неопределенные коэффициенты находят из тождества путем дифференцирования предыдущего выражения
|
Pn x |
|
Q |
|
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
ax2 bx c |
|
|
|
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ax |
2 |
bx c |
|
|
n 1 |
|
|
|
|
|
ax |
2 |
bx c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
после чего необходимо приравнять коэффициенты при одинаковых степенях неизвестной x, т.е. использовать метод сравнения.
Пример. Найти интеграл
I |
|
|
x2 |
||
|
|
|
|
dx. |
|
|
|
|
|
||
|
|
|
|||
|
1 |
2x x2 |
|||
|
|
|
61 |
|
|
Решение. Имеем
|
|
|
|
|
|
|
|
|
|
I Ax B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 2x x2 |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
2x x2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
после дифференцирования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
A 1 2x x2 Ax B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
1 2x x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 2x x2 |
|
|
|
|
1 |
2x x2 |
|
|
|
||||||||||||||||||||||||||||||
т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x2 A 1 2x x2 |
|
|
|
|
Ax B |
|
|
1 x |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
x2 A 2 Ax Ax2 Ax Ax2 B Bx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
x2 2 Ax2 3A B x A B ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
1 2 A; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
3A B; |
|
A |
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
; B |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
A B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
I |
|
|
|
x |
|
1 2x x2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
1 2x x2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
2 x 1 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2arcsin |
|
x 1 |
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
18.2. Дробно-линейная подстановка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax b |
|
|
|
|
|
|
|
|
ax b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Интегралы типа R x, |
|
|
|
|
|
|
|
|
|
,..., |
|
|
|
|
|
|
|
|
dx, где a,b,c, d |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cx d |
|
|
|
|
|
|
|
|
cx d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
действительные числа, |
, ,..., , натуральные |
числа, |
сводятся к |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
интегралам от рациональной функции путем подстановки:
ax b tk , cx d
где k наименьшее общее кратное знаменателей дробей 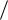 ,...,
,..., 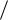 .
.
62

|
|
|
|
|
следует x |
b dtk |
|
|
Действительно, из |
подстановки |
|
и |
|||
|
|
||||||
|
|
ct k a b dt k ckt k 1 |
|
ctk a |
|||
dx |
d ktk 1 |
|
|
|
|||
|
|
|
dt, т.е. |
x и dx выражаются через |
|||
|
ctk a 2 |
|
|||||
|
|
|
|
|
|
|
|
рациональные функции от t.
При этом и каждая степень дроби ax b выражается через cx d
рациональную функцию от t.
Пример. Найти интеграл
dx
I 3 x 2
x 2 
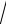 x 2 .
x 2 .
Решение. Наименьшее общее кратное знаменателей дробей
2
3
и1 есть 6
2
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x 2 t6 ; |
x t6 2; |
dx 6t5dt; |
t 6 x 2 |
|
|
|||||||||
I |
|
6t5dt |
6 |
|
t2 |
dt 6 t2 1 1dt 6 |
|
t 1 |
|
1 |
dt 3t2 |
6t |
||||
|
|
|
|
|
|
|
|
|||||||||
|
t4 t3 |
t 1 |
|
t 1 |
|
|
|
|
|
|
|
|||||
|
|
t 1 |
|
|
||||||||||||
6ln t 1 C 33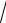 x 2 66
x 2 66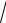 x 2 6ln
x 2 6ln 
 6
6 x 2 1 C.
x 2 1 C.
18.3. Тригонометрическая подстановка |
|
|
|
Интегралы типа |
|
|
|
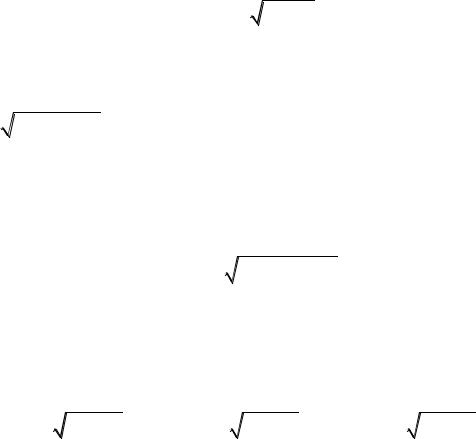
R x, a2 x2 dx; |
R x, a2 x2 dx, |
R x, |
x2 a2 dx |
приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью тригонометрических подстановок
x a sin t; |
x a tgt; |
x |
a |
. |
|
||||
|
|
|
sin t |
|
|
63 |
|
|
|
Пример. Найти интеграл
|
|
|
|
|
|
I |
|
4 x2 |
dx. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. x 2sin t; |
dx 2cost dt; |
t arcsin |
x |
. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I |
|
4 4sin |
2 t |
2cost dt |
|
|
4cos2 t |
dt |
1 sin2 t |
dt |
|
dt |
dt |
|
|
||||||||
|
4sin2 t |
|
|
4sin2 t |
|
sin2 t |
sin2 t |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
||
|
|
|
|
|
|
ctgt t C C arcsin |
|
|
ctg arcsin |
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
||
18.4. Интегралы типа R x, |
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||
ax2 |
bx c |
|
|
|
|
|
|
|
|
|
|||||||||||||
Выделив под радикалом полный квадрат и сделав подстановку
x |
b |
t, |
интегралы указанного типа можно привести к интегралам |
|||||||||
2a |
||||||||||||
|
|
|
|
dt; |
|
|
dt, |
|
|
dt. |
||
вида R t, |
|
|
R t, |
|
R t, |
|
||||||
|
a2 t2 |
a2 t2 |
t 2 a2 |
|||||||||
18.5. Интегрирование дифференциального бинома
Интегралы типа xm a bxn p dx (называются интегралами от
дифференциального бинома), где a,b действительные числа; m, n, p рациональные числа, берутся лишь в случае, когда хотя бы одно
из чисел p, |
m 1 |
или |
m 1 |
p |
является целым. |
|||
|
|
|
||||||
|
|
n |
n |
|
|
|||
Рационализация интеграла в этих случаях осуществляется |
||||||||
следующими подстановками: |
|
|
||||||
1) если p целое число, |
то |
x tk , где k наименьшее общее |
||||||
кратное знаменателей дробей m и n ; |
||||||||
2) если |
m 1 |
целое число, |
то a bxn t s , где s знаменатель |
|||||
|
||||||||
|
|
n |
|
|
|
|
||
дроби p;
64
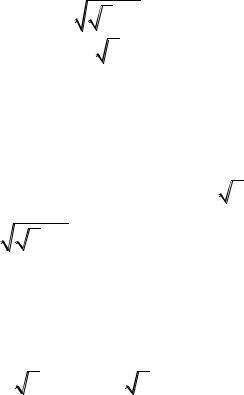
3) если |
m 1 |
p целое |
|
|
число, |
|
|
то a bxn xnt s , |
|
где |
s |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
знаменатель дроби |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример. Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
x |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Т.к. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I x |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
dx, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||||
то m |
; |
|
n |
; |
|
|
p |
; |
|
|
|
2 |
|
1 4 x t3; |
x |
t3 1 |
; |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
3 3t 2dt; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
dx 4 |
|
t3 |
1 |
|
|
t 3 4 x 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Т.о. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
I |
|
|
|
|
|
|
t |
|
|
|
12t |
2 |
|
t3 |
1 |
3 dt 12 |
|
|
|
t6 |
|
t3 |
|
dt 12 |
t7 |
12 |
t 4 |
C |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
t |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
4 |
|
1 |
|
3 4 |
|
1 |
|
C. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Глава 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
19. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
19.1. Определение интеграла по Риману
Прежде всего введем понятие разбиения отрезка a,b :
a x |
x |
... x |
x |
b |
или |
кратко |
x |
i k |
, |
причем |
|
0 |
1 |
k 1 |
k |
|
|
|
|
i |
i 0 |
|
|
xi 1 , xi отрезок разбиения , |
xi |
xi |
xi 1. |
|
|
|
|
||||
Величину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max x |
|
|
|
|
||
|
|
|
|
|
|
|
i |
|
|
|
|
i 1,k
будем называть мелкостью разбиения .
65
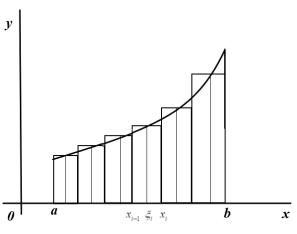
Пусть |
теперь |
дана |
f x , |
x a,b и |
пусть |
имеется |
некоторое |
|||||||||||
разбиение |
для a,b (рис. 4). Пусть i |
xi 1, xi , |
тогда |
составим |
||||||||||||||
сумму |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
f ; 1,..., k |
f |
i xi , |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
которая называется интегральной суммой Римана. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
Если |
f x 0, |
то |
каждое |
||||||
|
|
|
|
|
|
|
слагаемое |
|
|
равно площади |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямоугольника |
с |
|
основанием |
||||||||
|
|
|
|
|
|
|
xi и с высотой |
f i . |
|
|||||||||
|
|
|
|
|
|
|
|
|
Вся |
сумма |
|
равна пло- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щади ступенчатой фигуры. |
|||||||||||
Рис. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. |
f x называется интегрируемой (по Риману) на |
|||||||||||||||||
a,b , если A ; n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
x i n i kn |
, |
n 1,2,..., |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
причем lim |
0, и |
n : |
|
n x n , x n |
|
|
|
|
|
|
|
|
|
|||||
n |
n |
i |
|
i |
|
i 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
kn |
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
lim f |
|
|
|
A, |
|
|
|
|
|
|
||||||
|
|
i |
xi |
|
|
|
|
|
|
|||||||||
|
|
n |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где xi n xi n xi n1 . При выполнении вышеперечисленных условий
число А называется (римановым) определенным интегралом и обо-
значается через
b
f x dx,
a
где x переменная интегрирования, f x подынтегральная функция; a,b нижний и верхний пределы интегрирования; a,b промежуток интегрирования.
66

19.2. Ограниченность интегрируемой функции
Теорема. Если функция интегрируема на некотором отрезке, то она ограничена на этом отрезке.
□ Доказательство от противного, т.е. пусть f x , |
x a,b не |
ограничена и пусть
x i ii 0k ,
всилу неограниченности f x на a,b , она, по крайней мере, не
ограничена на |
каком-то отрезке |
|
разбиения, например, на x0 , x1 , |
||||
n |
x0 , x1 |
; |
n 1, 2,..., что |
|
|
|
|
т.е. 1 |
|
|
|
|
|||
|
|
|
lim f n |
. |
|||
|
|
|
n |
|
1 |
|
|
k
Но, по определению интеграла по Риману, f i xi будет
i 2
иметь определенное значение , тогда
|
|
|
|
|
|
n |
|
|
k |
|
|
|
i |
|
|
|
|
lim |
|
lim |
|
f |
|
|
|
x |
|
f |
|
x |
|
, |
|
||
n |
n 2 |
|
1 |
|
1 |
|
|
i |
|
|
|||||||
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
||
а это значит, что |
f x неинтегрируема. |
|
|
|
|
|
|
|
■ |
||||||||
Замечание. Обратное утверждение неверно. Контрпримером |
|||||||||||||||||
служит функция Дирихле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
f x |
1, |
|
если x рационально |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
если x иррационально. |
|
|
|
|||||||||
Действительно, если |
i |
выбрать |
рациональными, то |
1, |
|||||||||||||
а если i выбрать иррациональными, |
то |
0, а это означает, |
что |
||||||||||||||
предела нет.
19.3. Верхние и нижние суммы Дарбу. Верхний и нижний интегралы Дарбу
Пусть f x , |
x a,b и есть x i ii 0k , |
тогда, положим, |
||||||
|
|
sup f x , |
|
|
f x ; |
|
|
|
Mi |
|
mi |
inf |
i 1, k. |
||||
|
|
xi 1 x xi |
|
xi 1 x xi |
|
|
|
|
|
|
|
67 |
|
|
|
|
|
Составим
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
S |
S f |
Mi xi ; |
s |
s f mi xi ; |
|||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
i 1 |
очевидно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s S . |
|
|
|
|
|
|
Назовем |
S и |
s |
соответственно |
верхней и нижней суммами |
|||||||||
Дарбу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства сумм Дарбу |
||||||||
1. Если |
f x |
ограничена, то |
|
S и s определены. |
|||||||||
|
f x : Mi , mi |
i |
|
конечны, и поэтому |
|||||||||
□ В силу ограниченности |
1, k |
||||||||||||
S и s также конечны. |
|
|
|
|
|
|
|
|
■ |
||||
2. Если |
|
|
|
, то S |
S |
и s s |
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
□ Пусть |
|
|
|
|
|
|
xj |
|
|
|
|
|
|
|
|
|
|
|
|
i k |
|
j k |
|
|
|
||
|
|
|
x i i 0 и |
j 0 |
|
, тогда |
|||||||
|
|
|
|
|
f x , |
|
|
|
|
|
|
inf f x , |
|
|
|
|
mi |
|
inf |
|
i 1,k; |
|
|
|
|||||||||
|
mj |
j 1,k . |
||||||||||||||
|
xi 1 x xi |
|
|
|
|
|
|
|
x j 1 x x j |
|
|
|
|
|||
Т.к. |
x |
1 |
, x |
|
x |
, x |
, то m m . |
Кроме того, |
|
|
|
|||||
|
j |
j |
|
i 1 |
i |
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
xj , |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ji |
|
|
|
|
|
|
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
k |
|
|
k |
|
k |
|||
s mi xi |
mi x j |
mi x j |
mj |
x j |
mj x j |
|||||||||||
|
|
|
|
|
|
i |
|
|
|
|
i |
i |
i |
|
|
|
i 1 |
|
|
i 1 ji |
|
|
i 1 ji |
|
i 1 ji |
|
j 1 |
||||||
Аналогично доказывается, что S |
S . |
|
|
|
|
|||||||||||
Следствие. 1, 2: a,b s 1 |
S 2 . |
|
|
|
|
|||||||||||
□Положим, 1 и 2 , и воспользуемся свойством 2.
суммы Римана и Дарбу связаны неравенствами
|
|
s S . |
|
3. Если |
|
интегральная сумма Римана для , то |
|
|
|
|
|
|
|
s inf , |
S sup . |
|
|
1 ,... k |
1 ,... k |
|
|
|
|
s .
■
■
68
□ Пусть x |
i k |
|
для a,b и |
|
x |
|
1 |
, x |
и пусть |
|
X |
|
числовые |
|||||||||||||||||
|
i |
|
i 0 |
|
|
|
|
|
|
|
|
i |
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
i |
|
||
множества, ai |
const 0, то для множества |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
X x: x ai xi , xi Xi , i |
1, k |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
справедливы равенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||||
|
sup X ai |
sup Xi ; |
|
inf X ai inf Xi . |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
s mi xi |
inf |
f i |
xi |
inf |
|
f |
i xi |
inf |
|
. |
||||||||||||||||||||
i 1 |
i 1 |
x |
|
|
x |
|
|
|
x |
|
|
x |
|
i 1 |
|
|
|
|
|
x |
|
|
x |
|||||||
i 1 |
|
|
i |
|
i |
|
|
|
i 1 |
i |
|
i |
|
|
|
|
|
|
i 1 |
i |
|
|
i |
|||||||
Аналогично |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
S Mi xi |
sup |
f i xi |
|
|
sup |
|
f i xi |
|
|
sup . ■ |
||||||||||||||||||||
i 1 |
i 1 xi 1 i xi |
|
|
|
xi 1 i xi |
i 1 |
|
|
|
|
|
|
xi 1 i xi |
|||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. S s |
i |
|
f xi , где i |
f колебание |
f |
на xi 1, xi . |
||||||||||||||||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
□ Пусть X ,Y числовые множества и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
Z z: z x y, |
|
x X , |
y Y , |
|
|
|
|
|
|
|||||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sup Z sup X inf Y. Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Mi |
|
mi |
sup |
|
f x |
|
inf |
f x |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
xi 1 i xi |
|
|
|
|
|
xi 1 i xi |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x f x |
|
|
|
f , |
|
|
|
|
|
|
|
|||||||||||
|
|
|
sup |
|
|
|
f |
|
|
|
i 1,k |
|
|
|
|
|||||||||||||||
|
xi 1 x i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
xi 1 x i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
s |
Mi |
mi xi |
i f xi . |
|
|
|
■ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|||||
Определение. |
I |
* |
sup s , |
I |
* inf S |
называются |
соответственно |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нижним и верхним интегралами Дарбу, причем I* I *.
69

19.4. Необходимые и достаточные условия интегрируемости
Теорема. Для того чтобы ограниченная на некотором отрезке функция была интегрируемой на нем, необходимо и достаточно
lim S s 0.
0
Иными словами, 0 ,что : выполняется нера-
венство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S s |
|
, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
но т.к. s S , то окончательно S s . |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
□ Доказательство необходимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть для f x |
I b f |
x dx существует, т.е. |
lim |
|
I |
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
, то |
|
|
|
|
I |
|
|
или I |
|
I . |
||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
По свойству 2 сумм Дарбу имеем
I s S I
или 0 S s 2 .
Доказательство достаточности.
Пусть для f x выполнено условие lim S s 0. Из определения
0
нижней и верхней сумм Дарбу имеем
|
|
|
|
|
s |
I |
* |
I * S , |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда 0 I * I |
* |
S |
s |
|
|
|
I |
* |
I * I , |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
I S , |
|
|
|
|
|||||
что равносильно двум неравенствам |
|
|
|
|
||||||||||||
|
|
0 I s S |
s ; |
0 S |
I S s . |
|
||||||||||
Поэтому |
lim I s lim S I 0, |
|
|
|
|
|||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. lim s |
lim S |
I , но s |
|
|
S |
|
lim |
|
0. |
■ |
||||||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70
