Учебное пособие 800396

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

d 2 y d f x dx f x d dx

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

2.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

8.5. Таблица производных основных элементарных функций

Таблица 1

loga x

sin x

cos x

ax ln a

cos x

sin x

x ln a

tg x

ctg x

arcsin x

arccos x

arctg x

arcctg x

cos2 x

sin2 x

1 x2

ex e x

sh x

ch x

th x

cth x

sh x

ch x

sh x

ch x

ex e x

9.ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ И ПАРАМЕТРИЧЕСКИ ЗАДАННЫХ ФУНКЦИЙ

9.1. Неявно заданная функция

Если функция задана в виде y f x , то говорят, что она задана

в явном виде.

Определение. Под неявным заданием функции понимаем задание функции в виде уравнения F x, y 0, не разрешенного

относительно y.

Алгоритм вычисления производной от такой функции следующий: продифференцировать уравнение F x, y 0 по x, рассматри-

вая при этом y как функцию от x, и полученное затем уравнение разрешить относительно y .

9.2. Функция, заданная параметрически

x x t ;
Пусть	где t – вспомогательная переменная.
y y t ,
	31

Найдем y	. Для этого предположим,				что x t , y t дифферен-
x
цируемы, причем t x ,		тогда
			1	.


		tx	xt
			xt
Запишем y f x f x , откуда

					yt	.

	yx	ft tx		yx	xt
					xt

9.3.Логарифмическое дифференцирование

Рассмотрим функцию y uv , где u u x , v v x , тогда

ln y v ln u

y v ln u

v 1

ln u

v u

y v

ln u v

u .

10. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ

10.1. Производные высших порядков явно заданной функции

Определение. Производной n-го порядка (или n-ой производ-

ной) называется производная от производной (n – 1) порядка: y n y n 1 .

Производные порядка выше первого называются производными высших порядков.

10.2. Механический смысл производной второго порядка

Пусть в момент времени t скорость	материальной точки V,
а в момент t t скоростьV V , тогда	V	среднее ускорение
	t

точки за t.

lim V a ускорение в точке,

t 0 t

но

lim S V ,

t 0 t

поэтому

St Vt a.

Вывод. Вторая производная от пути по времени есть величина ускорения прямолинейного движения точки.

10.3. Производные высших порядков неявно заданной функции

Имеем F x, y 0, тогда, продифференцировав его по x, получим выражение, в которое войдут x, y, y . Вновь продифференцируем по x как неявную функцию и получим y .

10.4.Производные высших порядков от функций, заданных параметрически

			x x t ;		y	yt	.
Пусть	y y			тогда
					x
		x :				xt
			y y t ,


					t
				yx	t	, и т.д.
Найдем вторую производную yx	yx x	yx t	tx	xt		, и т.д.
				xt

11. ДИФФЕРЕНЦИАЛ ФУНКЦИИ

11.1. Понятие дифференциала функции

Пусть y f x имеет в точке x отличную от нуля производную,

т.е.

lim y f x 0,

x 0 x

тогда, по теореме о связи функции, ее предела и б.м.ф., имеем

y f x x x,

где б.м.ф.

Определение. Дифференциалом функции y f x в точке x

называется главная часть ее приращения dy f x x,

где dy дифференциал первого порядка.

Пусть y x, тогда dy dx, поэтому окончательно

dy f x dx.

Отсюда следует

fx dydx .

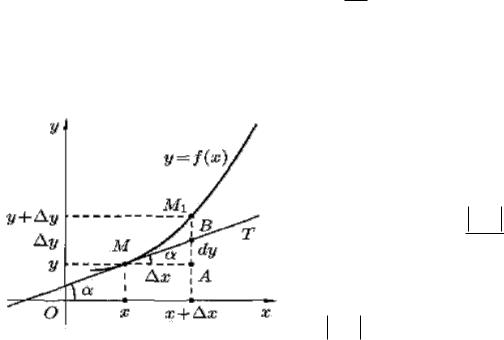
11.2.Геометрический смысл дифференциала функции

T – касательная в точке M x, y .

Из MBA

AB tg x ,

т.е.

AB tg x f x dx dy,

Рис. 1

т.е. дифференциал функции y f x в точке x равен приращению

ординаты касательной к графику функции в этой точке, когда x получит приращение x (рис. 1).

11.3. Основные теоремы о дифференциалах

Теорема.

d u v du dv; d uv v du u dv;

u	v du u dv			v 0
d
d		v	2
v		v
						■
□ d uv uv		dx u v uv			dx vu dx uv dx vdu udv.	■

Остальные доказываются аналогично.

Теорема. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

□ Пусть y f u		и u x , т.е.	y f x , тогда	y	y	u	, но
				x	u	x
							■
yx dx yu	ux dx, т.е. dy yu du.						■

11.4. Дифференциалы высших порядков

Пусть y f x , тогда dy f x dx, поэтому

d dy d f x dx

f x dxdx

Обобщая этот результат, получим

d n y f n x dxn .

12.ИССЛЕДОВАНИЕ ФУНКЦИЙ ПРИ ПОМОЩИ ПРОИЗВОДНЫХ

12.1. Некоторые теоремы о дифференцируемых функциях

Теорема Ролля. Если f x непрерывна на a,b , дифференцируема на a,b ; f a f b , то c a,b ,в которой f c 0.

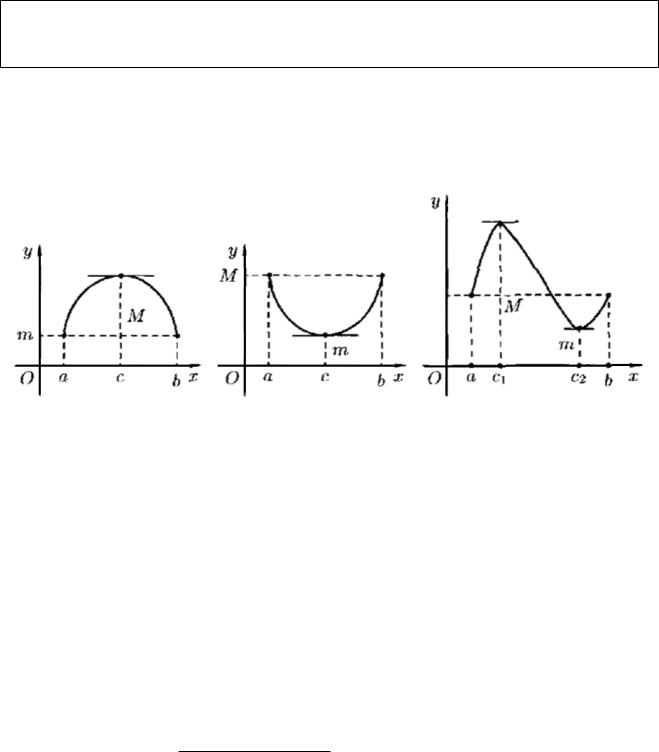
□ Т.к. f x непрерывна на a,b , то M max f x , m min f x ;

M , m a,b (если M m, то f x const f x 0 x a,b ). Если M m, то M или m a,b (рис. 2), т.к. f a f b .

		Рис. 2
Пусть, например, М в	точке x c a,b , т.е.			f c M . Тогда
x a,b :
f c f x .

Найдем f x в точке с:
		f c x f c	,

f c lim		x
x 0		x

откуда f c x f c 0.

Если x 0 (справа точки с), то

fc x f c 0, f c 0 .

Если x 0 (слева точки с)

	f c x f c	0, f c 0
	x

f c 0.		■

Теорема Коши. Если f x и x непрерывны на a,b , диффе-

ренцируемы на a,b , причем x 0 x a,b , то c a,b , для

которой

b f a

f c

b a

□ Отметим, что b a 0, т.к.

по теореме Ролля нашлась бы

точка c: c 0.

Рассмотрим вспомогательную функцию:

F x f x f a

f b f a

x a .

b a

F x удовлетворяет условиям теоремы Ролля, тогда c:

c a,b , что

F c 0, но

f b f a

x f

x b a

x ,

f b f a

c f

c 0,

b a

f b f a

f c

■

b a

Теорема Лагранжа.

Если f x непрерывна на a,b ,дифферен-

цируема на a,b , то c a,b , что

f b f a f c b a .

□ Положим, x x, тогда, воспользовавшись доказательством теоремы Коши, находим

b a b a;				x 1;		c 1,
откуда		f b f a
		f b f a			f c
					f c
			b a

f b f a f c b a .								■
Следствие 1. Если	f x 0,			x a,b , то f x const.
□ Пусть f x 0, a,b . Возьмем произвольные x1							и x2 из a,b ,
и пусть x1 x2 , тогда по теореме Лагранжа c x1, x2 ,							что
f x2 f x1 f c x2 x1 ,
но f x 0 f c 0,			где	x1 c x2		f x2 f x1 0,		т.е.
f x2 f x1 ,а т.к. x1, x2 – произвольные из a,b ,то f x const.								■
Следствие 2. Пусть
Следствие 2. Пусть		f1	x f2 x , x a,b , тогда

f2 x f1 x const.


□ f2 x f1 x			по сл. 1	f2 x f1 x const. ■
	f2	x f1 x 0,

12.2. Правило Лопиталя

Теорема (Правило Лопиталя раскрытия неопределенностей

вида

). Пусть f

x и x непрерывны и дифференцируемы в окре-

и f x0 x0 0.

Пусть x 0 в окрестности

стности точки x0

точки x0. Если существует предел

lim

то

x x0

lim

f x

lim

x x0

□ Применим к f x и x теорему Коши для x0 , x , тогда

f x f x0

, c x , x

x x0

или, учитывая f x0 x0 (по условию теоремы):

f x

f c

Пусть x x0 , тогда c x0 , поэтому c x

lim

f x

lim

■

x x0 x

x x0

Теорема (Правило Лопиталя раскрытия неопределенностей

вида

). Пусть

f x , x

непрерывны

дифференцируемы

lim f x

окрестности

точки x0

этой

окрестности

x x0

lim x , x 0. Тогда если существует предел

lim

то

x x0

lim

f x

lim

x x0

(Без доказательства)

12.3. Возрастание и убывание функций

Установим необходимые и достаточные условия возрастания и убывания функции.

Теорема (необходимые условия). Если дифференцируемая на
a,b f x возрастает (убывает), то f x 0			f x 0 x a,b .

□ Пусть f x возрастает	a,b . Возьмем		x и x x, x a,b
и x x a,b . Рассмотрим
y	f x x f x	.

x	x

	Если x 0,			то x x x и f x x f x ;
если x 0,			то	x x x и		f x x f x ,		тогда	y 0,	т.к.
									x
числитель и знаменатель имеют одинаковые знаки, тогда
					lim	y f x 0.				■
					x 0	x
	Аналогично доказывается случай убывания f x .

	Теорема (достаточные условия). Если f x							дифференцируема
на	a,b	и	f x 0		f x 0 x a,b ,		то	f x	возрастает
(убывает) на a,b .

□	Пусть	f x 0. Возьмем				x1 a,b , x2 a,b , причем x1 x2 .
Применим к x1, x2 теорему Лагранжа:
			f x2 f x1 f c x2 x1 , где c x1, x2 .
Т.к. f c 0, x2 x1 0					f x2 f x1 0		f x2 f x1 .			■

12.4. Максимум и минимум функций

Определение. Точка x0 называется точкой максимума

y f x , если существует такая окрестность точки x0 , что x x0: f x f x0 .

Аналогично определяется точка минимума. Максимум и минимум называются экстремумом.

Теорема (необходимое условие экстремума). Если дифферен-

цируемая функция y f x имеет экстремум в точке x0, то							f x 0.
цируемая функция y f x имеет экстремум в точке x0, то							f x 0.

□ Пусть точка x0 – точка максимума, тогда
	f x0		f x0 x ,
но y	f x0 x f x0	0,	если x 0 и	y	0,	если x 0.
но y		0,	если x 0 и	x	0,	если x 0.
x	x			x
			40

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20222.17 Mб3Учебное пособие 800391.pdf
#
01.05.20222.19 Mб2Учебное пособие 800392.pdf
#
01.05.20222.21 Mб6Учебное пособие 800393.pdf
#
01.05.20222.21 Mб5Учебное пособие 800394.pdf
#
01.05.20222.22 Mб19Учебное пособие 800395.pdf
#
01.05.20222.23 Mб6Учебное пособие 800396.pdf
#
01.05.20222.24 Mб5Учебное пособие 800397.pdf
#
01.05.20222.27 Mб10Учебное пособие 800398.pdf
#
01.05.20222.27 Mб7Учебное пособие 800399.pdf
#
01.05.2022158.06 Кб2Учебное пособие 8004.pdf
#
01.05.2022349.85 Кб2Учебное пособие 80040.pdf