Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 800396

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

2.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 106 7 8 9 10 > Следующая >>>

Теорема (основная теорема алгебры). Всякий Pn x , n 0

имеет по крайней мере один корень (действительный или комплексный).

(Без доказательства)

Теорема. Всякий многочлен Pn x

можно представить в виде

Pn x a0 x x1 x x2 ... x xn ,

где x1, x2 ,...xn корни многочлена.

□ Пусть

Pn x : Pn x1 0,

тогда

x x x1 Pn 1 x ,

но

Pn 1 x : Pn 1 x2 0,

тогда

Pn x x x1

x x2 Pn 2 x

т.д.

Продолжая этот процесс, получим

Pn x a0 x x1 x x2 ... x xn .

■

Определение. Множители вида x xi будем называть линей-

ными.

Если в разложении Pn x

линейный множитель встречается k

раз, то такой корень называется корнем кратности k.

Теорема. Если Pn x 0, то ai

0, n

Теорема. Если Pn x Qn x ,

то ai

0, n

Теорема. Всякий многочлен Pn x

может быть представлен в

виде

x a

x x

k1 x x k2

... x x kr

x2 p1x q1 s1 ... x2

pm x qm sm ,

при этом k1 k2 ... kr 2 s1

s2 ... sm .

Определение. Дробно-рациональной функцией (или рациональ-

ной дробью) называется функция

f x Pm x .

Qn x

Рациональная

дробь

называется правильной,

если m n,

в противном случае – неправильной.

Утверждение. Пусть даны Pm x и Qn x , m n,

тогда

Pm x

Lm n x

Rk x

k n .

Qn x

Это можно сделать путем деления Pm x

на Qn x в столбик.

Определение. Правильные рациональные дроби вида

;

k 2 ;

III

Mx N

p2 4q 0 ;

x a

x a k

x2 px q

Mx N

4q 0

называются

простейшими

px q k

рациональными дробями I, II, III, IV типов.

Теорема.

Всякую правильную

рациональную

дробь

P x

Q x ,

знаменатель которой разложен на множители

Q x x x1 k1

x x2 k2 ... x2 p1x q1 s1

... x2 pm x qm sm ,

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

P x				A1				A2				...				Ak1
Q x			x x1					x x		2		...			x x			k1
									1								1
								B				B			2 ...				Bk				k2	...
							x x2					x x			2 ...				x x				k2	...
							1						2								2
														2							2
...			C x D									C x D						...					Cs		x Ds			...
				1			1					2			2									1	1
		x2		p1x q1						x2 p1x q1 2										x2 p1x q1						s1
...			M		1	x N						M	2	x N			2		...					M s x Ns			m
					1		1						2				2								m		m
																													.
	x2			pm x qm							x2 pm x qm 2											x2			pm x qm sm				.

Пример.
				x2 4								A					B					C				D
1)																											;
1)	x 2 x 3 3									x 2					x 3						x 3 2			x 3 3			;
2)			x3		1			A			B		Cx D							;
2)		2			2							2				2	1			;
		2			2	1		x			x	2		x		2
	x x							x			x			x
	x x
3)						7x2	8x 9												A				B		Cx D					Mx N			.
3)															2										2							2	.
																		x		1			x 2		x x			1
		x 1 x 2 x							2	x 1								x		1			x 2		x x			1	x	2	x 1
									2																					2

Для нахождения A1, A2,…, B1, B2,… (см. теорему) можно применить метод сравнения коэффициентов. Суть метода такова:

1.Правую часть приведем к общему знаменателю.

2.Т.к. в полученном тождестве знаменатели равны, то тождественно равны и числители.

3.Приравнивая коэффициенты при одинаковых степенях, получим систему линейных уравнений, из которой и определяются неизвестные коэффициенты разложения.

Пример. Представить дробь

2x2 3x 3

x 1 x2 2x 5

ввиде суммы простейших дробей.

Решение:

2x2 3x 3

Bx C

, т.е.

x 1

x 2x 5

x 1

2x 5

2x 3x 3

A x

2x 5

x 1 Bx C

;

x 1

x2 2x 5

x 1

2x 5

2x2 3x 3 Ax2 2Ax 5A Bx2 Bx Cx C,

т.е. 2x2 3x 3 A B x2 2A B C x 5A C ,

2 A B,

A 1; B 3; C 2

3 2A B C,

3 5A C,

2x2 3x 3

3x 2

x 1

x 2x 5

x 1 x

2x 5

16.2. Интегрирование простейших рациональных дробей

Найдем интегралы от простейших рациональных дробей.

dx A

d x a

Aln

x a

II.

dx A x a

d x a

k 1

x a k

k 1

III. J

Mx N

px q

= x

=t,

x=t

dx=dt;

=a2 =

M t

t dt

dt = M

t2 a2

t 2 a2

ln t2

arctg

ln x2 px q2

arctg

IV.

Mx N

dx,

k 2,

x2 px q k

Данный интеграл подстановкой x 2p

интегралов:

t dt

t2 a2

Вычислим первый интеграл:

= t сводится к сумме двух

a2 q p2 . 4

t dt

d t2 a2

k 1

2 1 k

t a

Вычислим второй интеграл:

1 t2 a2 t2

t2dt

t2 a2

k 1

t2 a2

Найдем

u t

du dt

tdt

t 2

d t 2

t2 a2

k 1

2 1 k

	t						1			dt			.

					k 1		1 k					k 1
		2		2		2	1 k		2		2
2 1 k	t	2	a	2				t	2	a	2
2 1 k	t		a					t		a

Дальнейшие действия очевидны.

17.ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ

17.1. Универсальная тригонометрическая подстановка

Вычисление неопределенных интегралов типа

R sin x,cos x dx

сводится к вычислению интегралов от рациональной функции подстановкой

tg 2x t,

которая называется универсальной. Действительно,

2 tg

tg2

1 t2

sin x

;

cos x

;

2 x

1 t2

1 tg

x 2arctgt;

dt, поэтому

1 t2

1 t

R sin x,cos x dx R

;

dt R1 t dt.

1 t

Здесь R1 t – рациональная функция от t. Обычно этот способ весьма

громоздкий, зато он всегда приводит к результату.

На практике применяют и другие, более простые подстановки, в зависимости от свойств и вида подынтегральной функции. В частности, удобны следующие правила:

1) если R sin x,cos x нечетна по sin x, т.е.

R sin x,cos x R sin x,cos x ,

то подстановка cos x t;

2) если R sin x,cos x нечетна по cos x, т.е.

R sin x, cos x R sin x,cos x ,

то подстановка sin x t;

3) если R sin x,cos x четна по sin x и cos x, т.е.

R sin x, cos x R sin x,cos x ,

то подстановка tg x t. Такая же подстановка применяется, если

R tg x dx.

Пример. Найти интеграл

3 sin x cos x

Решение: t tg

тогда

dt;

sin x

;

cos x

1 t2

;

1 t2

2dt

3 sin x cos x

1 t 2

3 3t 2 2t 1 t 2

1 t

																									1
				2dt								dt								d t
																				d t
																									2
			2 t 2 t 2							t2 t 2												1	2				7
																			t
																			t			2					4
																						2					4
					t	1													1 tg					x
		2			t								2						1 tg
		2		arctg	2			C					2		arctg								2			C.

		7			7								7									7
		7			7								7									7

					2
Пример. Найти интеграл
													dx					.

											1 sin2 x
Решение:
R sin x, cos x				1									1				R sin x,cos x , то

				sin2 x							sin2
		1		sin2 x					1		sin2					x
tg x t	x arctgt;				dx				dt			,		sin2 x							tg2 x							t2	,
tg x t	x arctgt;				dx		1 t2					,		sin2 x							1 tg2					x		1 t2	,
							1 t2														1 tg2					x		1 t2

		dt						dt			1			d		2t

					2		2t2		1							2

				t								2			2t
1 t2	1			t								2					1
1 t2	1			1 t		2											1
				1 t
	1							1		arctg
	1		arctg			2t C		1					2 tg x C.

	2								2
	2								2

17.2. Интегралы типа sinm x cosn x dx

Для нахождения таких интегралов используются следующие приемы:

1)подстановка sin x t, если n целое положительное нечетное

число;

2)подстановка cos x t,если m целое положительное нечетное

число; 3) формулы понижения порядка:

cos2 x

1 cos 2x ;

sin2 x

1 cos 2x ;

sin x cos x

sin 2x,

если m и n целые неотрицательные четные числа;

подстановка

tg x t,

если

m n четное неотрицательное

число.

Пример. Найти интеграл

sin4 x cos5 x dx.

Решение:

sin x t;

x arcsin t;

dt;

cos x 1 t 2 ,

sin4 x cos5 x dx t 4

1 t2

t 4 1 t 2 2dt t 4 2t6 t8 dt

1 t 2

sin5 x

sin7 x

sin9

x C.

Пример. Найти интеграл

sin4 x cos2 x dx.

Решение:

sin4 x cos2 x dx sin2 x cos2 x sin2 xdx 14 sin22x 12 1 cos 2x dx

sin22xdx

sin2

2x cos 2xdx

1 cos 4x dx

sin22xd sin2x

sin 4x

sin32x C.

Пример. Найти интеграл

cos 1x sin 3 x dx.

Решение: m n 4

tg x t;

x arctgt;

;

1 t2

sin x

;

cos x

, поэтому

t 2

1 t2

cos

x sin

x dx

dt t

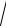1 t2 1 t2

21t2 ln t C 12 ctg2 x ln tg x C.

17.3.Использование тригонометрических преобразований

Интегралы типа

sin axcosbx dx,

cos axcosbx dx,

sin axsin bx dx

вычисляются с помощью известных формул тригонометрии:

sin x cos x

sin

sin ;

cos x cos x

cos cos

;

sin xsin x

cos

cos .

Пример. Найти интеграл

sin8x cos 2x dx.

Решение:

sin8x cos 2x dx

sin 6x sin10x dx

cos 6x

cos10x

18. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ

18.1. Квадратичные иррациональности

Рассмотрим некоторые типы интегралов, содержащих иррациональные функции

mx n

ax2 bx c dx,

dx,

ax2

bx c

ax2 bx c

которые называются неопределенными интегралами от ных иррациональностей.

Эти интегралы вычисляются следующим образом: 1) под радикалом выделить полный квадрат

ax2 bx c

b 2

a x2

a x

a 4a

2) сделать подстановку

квадратич-

		4ac b2

		4a2
		4a2

<<< < Предыдущая 1 2 3 4 56 / 106 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20222.17 Mб3Учебное пособие 800391.pdf
#
01.05.20222.19 Mб2Учебное пособие 800392.pdf
#
01.05.20222.21 Mб6Учебное пособие 800393.pdf
#
01.05.20222.21 Mб5Учебное пособие 800394.pdf
#
01.05.20222.22 Mб19Учебное пособие 800395.pdf
#
01.05.20222.23 Mб6Учебное пособие 800396.pdf
#
01.05.20222.24 Mб5Учебное пособие 800397.pdf
#
01.05.20222.27 Mб10Учебное пособие 800398.pdf
#
01.05.20222.27 Mб7Учебное пособие 800399.pdf
#
01.05.2022158.06 Кб2Учебное пособие 8004.pdf
#
01.05.2022349.85 Кб2Учебное пособие 80040.pdf