Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 800396

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

2.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

С другой стороны,			f x0 x f x0
f x0	lim				,
				x
	x 0
поэтому f x0 0, когда		x 0		и f x0 0, когда		x 0,
f x 0.						■

Теорема (достаточное условие экстремума). Если непрерыв-

ная функция y f x дифференцируема в некоторой окрестности точки x0 и при переходе через нее (слева направо) f x меняет знак

с ″+″ на ″-″, то x0 – точка максимума, с ″-″ на ″+″, то x0 – точка минимума.

(Доказательство очевидно)

Вывод. Исследовать функцию на экстремум означает найти все ее производные.

Теорема.

Если в точке x0 f x0 0 и f x0 0, то точка x0 –

максимум, если f x0 0; точка x0 – минимум, если

f x0 0.

□ Пусть f x0 0.Т.к.

f x0

lim

x f

lim

x0 x

т.е.

x 0

f x0

Т.о., если x 0,

то

f x0

x 0,

если x 0 , то

f x0 x 0, точка x0 – точка максимума. ■

12.5. Наибольшее и наименьшее значение функции на отрезке

Сформулируем правило нахождения наибольшего и наименьшего значений y f x на a,b .

1)найти критические точки функции на a,b ;

2)вычислить значение функции в найденных критических

точках;

3)вычислить значение функции при x a и x b;

4)среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

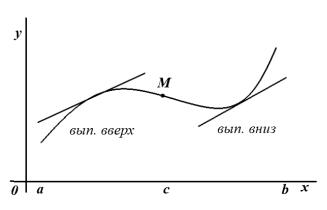
12.6.Выпуклость графика функции. Точки перегиба

Определение. График дифференцируемой функции y f x называется выпуклым вниз на a,b , если он расположен выше

любой ее касательной на этом интервале, а если ниже – выпуклым вверх. Точка графика, отделяющая части выпуклости, называется

точкой перегиба (см. на рис. 3 точку M).

		Рис. 3

Теорема. Если y		f x на a,b имеет f x 0,	то на a,b –
выпуклость вверх, если		f x 0 выпуклость вниз.

□ Пусть f x0 0	x a,b . Возьмем точку x0, тогда уравнение
касательной	yкас f x0 f x0 x x0
	yкас f x0 f x0 x x0
или		f x0 f x0 x x0 .
	yкас	f x0 f x0 x x0 .

Вычтем из y f x почленно уравнение касательной y yкас f x f x0 f x0 x x0 .

По теореме Лагранжа:						f x f x0 f c x x0 , где x0 c x,
тогда
y y		f	c x x	f x x x				f c	f x	x x .
кас			0			0	0		0		0
По теореме Лагранжа:					f c f x0 f c1 x x0 ,					x0 c1	c,
тогда					f c1 c x0 x x0 .
			y yкас
Если x x0			c x0			f c1 0		y yкас 0.
Если x x0			c x0			f c1 0		y yкас 0.			■

Теорема (достаточное условие существования точек пере-
гиба). Если f x при переходе через точку x0,									в которой f x 0
(или не существует), меняет знак, то точка x0 – точка перегиба.
□ Пусть	f x0 0 при x x0 , и						f x0 0 при x x0 . Это означает,

что слева от точки x0 – выпуклость вверх, справа – выпуклость вниз
M x , f x		точка перегиба.	■
0	0

12.7. Асимптоты графика функции

Определение. Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Прямая x a вертикальная асимптота, если

lim f x ,	или lim	f x ,	или lim f x .
x a	x a 0		x a 0

Рассмотрим вопрос о наклонной асимптоте, имеющей уравнение y kx b.

Пусть M x, y L : y f x , тогда расстояние от точки М до касательной

d kx y b , k 2 1

но из d 0 lim

kx y b 0, т.е.

kx y b x , где x б.м.ф.

Запишем

lim

x x

Т.к.

0, и

0, то

k lim

b lim kx y .

x x

В частности,

если k 0,

то b lim f x

, т.е.

y b горизон-

тальная асимптота.

12.8. Общая схема исследования функции и построения графика

Исследование y f x проводится в следующей последовательности:

1)найти область определения функции;

2)найти (если это можно) точки пересечения графика с осями координат;

3)найти интервалы знакопостоянства функции (промежутки,

на которых f x 0

или f x 0);

4)выяснить, является ли функция четной, нечетной или общего

вида;

5)найти асимптоты графика функции;

6)найти интервалы монотонности функции;

7)найти экстремумы функции;

8)найти интервалы выпуклости и точки перегиба графика функции.

13. ФОРМУЛА ТЕЙЛОРА

Для того чтобы вычислить значения y f x , ее заменяют многочленом Pn x степени n.

13.1. Формула Тейлора для многочлена

Пусть

f x

x a

a x a x2

... a xn .

Представим Pn x в виде

x A A

x x

x x 2 ... A

x x n .

Для нахождения A0 , A1,...An

продифференцируем Pn x :

x A 2A

x x

3A x x

2 ... nA

x x n 1

;

P x 2A 2 3A x x ... n n 1 A

x x

n 2 ;

……………………………………………………………

P n x n n 1 ...2 1A .

Возьмем x x0 ,

тогда

x A P

x 1!A P x ,

P x

2!A

P x ,

P x 2 3A P

x ,

……………………………………………………………

Pn n x0 n n 1 ...2 1An Pn n x0 ,

т.е.

Pn x Pn x0 Pn x0 x x0 Pn x0 x x0 2 ...

1! 2!

... Pn n x0 x x0 n формула Тейлора для многочленов. n!

13.2. Формула Тейлора для произвольной функции

Теорема. Если y f x

определена

некоторой

окрестности

точки x0

и имеет в ней

производные

до n 1 го порядка

включительно, то x из этой

окрестности найдется точка c x0 , x ,

такая, что

f x f x

x x

...

f n

x x

f n 1 c

x x

n 1

n 1 !

где c x0

x x0 ,

0 1.

Это формула Тейлора, а при x0 0 формула Маклорена.

R x

f n 1 c

x x

n 1

n 1 !

остаточный член.

Глава 2. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

14. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

14.1.Понятие неопределенного интеграла

Вдифференциальном исчислении решается задача: по данной функции f x найти ее производную (дифференциал). Интегральное

исчисление решает обратную задачу: найти функцию F x , зная ее производную F x f x (или дифференциал).

Определение. Функция F x называется первообразной функ-

ции для f x на a,b , если x a,b :

F x f x dF x f x dx .


Теорема. Если F x первообразная	для f x	на a,b , то
множество всех первообразных задается	формулой	F x С, где

С const.

□	F x С F x С f x . Пусть

	x f x ,тогда
	x f x ,тогда
		x F x	f x f x 0
		x F x	f x f x 0

теперь x F x	и
x F x C.	■

Определение.		Множество		всех	первообразных функций
F x С для	f x	называется неопределенным				интегралом от
функции f x и обозначается символом
			f x dx F x С.
f x подынтегральная			функция,	f x dx подынтегральное выра-
жение, x переменная			интегрирования,		знак	неопределенного

интеграла.

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Для всякой ли функции существует неопределенный интеграл? Имеет место утверждение: «Всякая непрерывная на a,b функ-

ция имеет на этом промежутке первообразную».

14.2. Свойства неопределенного интеграла

f x dx,

f x

1) d

f x dx

□ d

x dx d F x C dF x dC F x dx f x dx

x dx

F x C F x C

f x .

■

2) dF x F x C

□ dF x F x dx f x dx F x C.

■

3) f x dx f x dx,

0 постоянная

□

f x dx

F x dx

d F x F x C

F x

F x C

f x dx.

			f x dx	g x dx .
4)	f x g x dx
□ Пусть F x f x ,		G x	g x , тогда

■

f x g x dx

F x G x dx

x G x dx

d F x G x F x G x C F x

G x C

f x dx g x dx. ■

Если f x dx F x С,то и f u du F u С.

□ Пусть u x , тогда F u

F x

поэтому

dF u F u du f u du

u du

F u C.

d F u

■

14.3. Таблица основных неопределенных интегралов

Таблица 2

xn dx

xn 1

C n 1

n 1

tg x C;

cos2 x

dx x C

;

ctg x C;

sin2 x

Окончание табл. 2

ax dx

sin x

ln a

ex dx ex C;

cos x

sin xdx cos x C;

arcsin

a2 x2

cos xdx sin x C;

x2 a2

tg xdx ln

cos x

arctg

ctg xdx ln

sin x

a x

15. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

15.1. Метод непосредственного интегрирования

Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

15.2. Метод интегрирования подстановкой (заменой переменной)

Пусть требуется вычислить интеграл

f x dx.


Тогда x t		dx t dt и		f x dx		f t t dt.

15.3. Метод интегрирования по частям

Пусть u u x , v v x , тогда d uv udv vdu.

Интегрируя

d uv udv vdu, или udv uv vdu.

– формула интегрирования по частям.

Типы интегралов, которые удобно вычислять методом интегрирования по частям:

1. Интегралы вида P x ekxdx, P x sin kx dx, P x cos kx dx,

где P x многочлен, k const.

Удобно положить u P x , dv остальное.

2.Интегралы вида P x arcsin kx dx, P x arccos kx dx,

P x arctg kx dx, P x arcctg kx dx, P x ln x dx.

Удобно положить P x dx dv.

Интегралы вида eax sin bx dx, eax cosbx dx, a,b const.

За u eax .

16. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ

16.1.Понятие о рациональных функциях

Определение. Функция вида

P x a xn a xn 1 ... a						x a ,
	n	0	1	n 1		n
где n N, ai i
	0, n	постоянные		коэффициенты,			называется
многочленом, n степень многочлена.
Определение. Корнем многочлена называется x0: Pn x0 0.

Теорема. Если x1 корень Pn x ,				то	многочлен		делится без
остатка на x x1 .

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20222.17 Mб3Учебное пособие 800391.pdf
#
01.05.20222.19 Mб2Учебное пособие 800392.pdf
#
01.05.20222.21 Mб6Учебное пособие 800393.pdf
#
01.05.20222.21 Mб5Учебное пособие 800394.pdf
#
01.05.20222.22 Mб19Учебное пособие 800395.pdf
#
01.05.20222.23 Mб6Учебное пособие 800396.pdf
#
01.05.20222.24 Mб5Учебное пособие 800397.pdf
#
01.05.20222.27 Mб10Учебное пособие 800398.pdf
#
01.05.20222.27 Mб7Учебное пособие 800399.pdf
#
01.05.2022158.06 Кб2Учебное пособие 8004.pdf
#
01.05.2022349.85 Кб2Учебное пособие 80040.pdf