Момент силы относительно оси

Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси , взятому относительно точки пересечения оси с этой плоскостью.

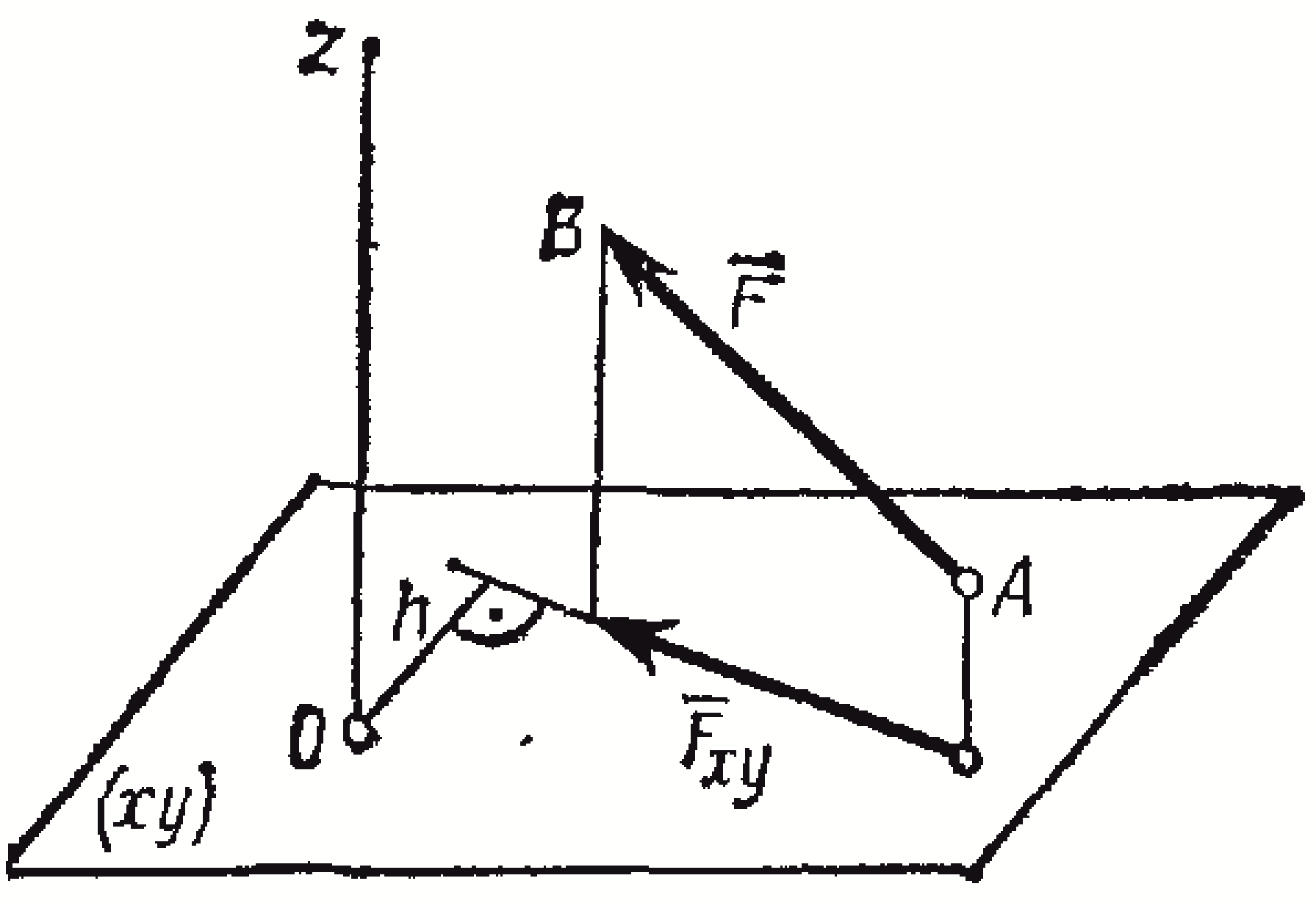
Момент силы относительно оси будет иметь знак плюс, когда с положительного конца оси поворот, который стремится совершить сила , виден происходящим против хода часовой стрелки, и знак минус — когда по ходу часовой стрелки.

Рис. 28

Равновесие пространственной системы сил

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю. Т.е

1.) , 2.) , 3.) ;

4.) , 5.) , 6.) .

Задача 7. Горизонтальная прямоугольная плита весом и толщиной (рис. 29) закреплена сферическим шарниром в точке , цилиндрическим (подшипником) в точке и невесомым стержнем . На плиту в плоскости , действует сила , а в плоскости , пара сил с моментом .

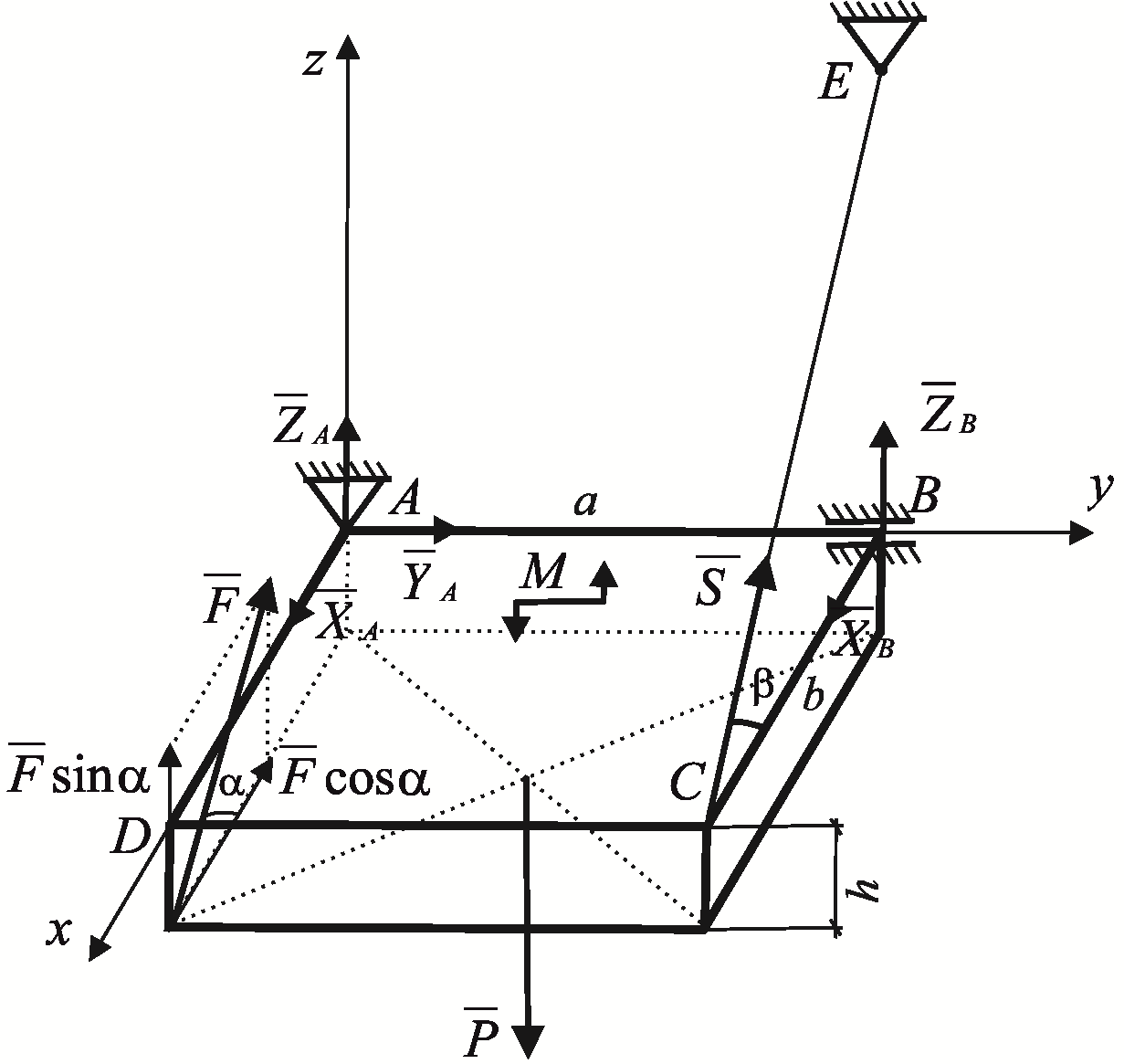
Рис. 29

Дано: , , , , , , , .

Определить реакции опор , , , , и усилие стержня .

Указание. Данная задача относится к теме о равновесия тела под действием произвольной системы сил. При её решении надо учесть, что реакция сферического шарнира имеет три составляющие, а реакция цилиндрического шарнира две составляющие, лежащие в плоскости, перпендикулярной оси шарнира. При вычислении момента силы часто удобно разложить её на две составляющие, параллельные координатным осям, и применить теорему Вариньона.

Решение. На плиту действуют заданные силы , и пара с моментом , а также реакции связей , , , , , . _{Для определения шести неизвестных реакций составляем шесть уравнений равновесия произвольной пространственной системы сил, действующих на плиту:}

: ;

: ;

: ;

: ;

: ;

: .

_{Подставим в составленные уравнения числовые значения всех заданных величин, получим:}

;

;

;

;

;

.

_{Решив систему алгебраических уравнений получим:}

_{, , , , , .}

Определение положение центра тяжести тела

Центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.

Некоторые способы определения положений центров тяжести тел:

Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.

Разбиение (задача 8). Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно.

Дополнение (задача 9). Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известные.

Задача 8. Определить координаты центра тяжести плоской фигуры, изображенной на рис. 30 при следующих данных ; ; .

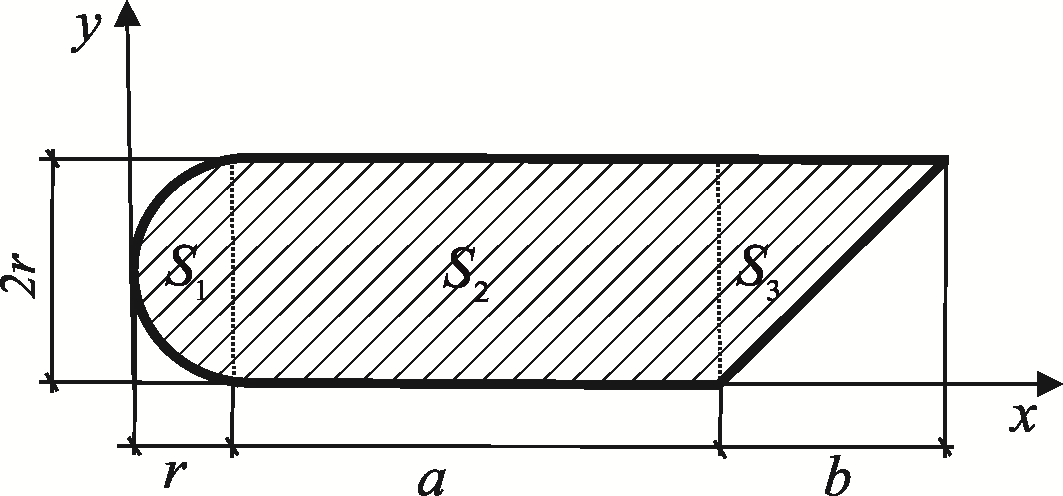
Рис. 30

Указания. В решении необходимо применить способ разбиения, при котором плоская фигура разбивается на простейшие части (прямоугольник, треугольник, полукруг), для которых положение центра тяжести известно:

для прямоугольника – на пересечении диагоналей;

для треугольника – на пересечении медиан. В частности, для прямоугольного треугольника центр тяжести находиться в точке пересечения отрезков, проведённых на расстоянии 1/3 длины соответствующего катета. Отрезки проводится от прямого угла параллельно катетам;

для полукруга – на оси симметрии полкруга на расстоянии от центра соответствующего круга. В общем случае, центр тяжести площади кругового сектора лежит на его оси симметрии, на расстоянии от центра равном (для полукруга ).

Решение. Фигура разбивается на три простейшие части: полукруг ( ), прямоугольник ( ), треугольник ( ), площади которых равны:

, , .

Центры тяжести рассматриваемых частей фигуры имеют следующие координаты:

для полукруга ( ): , ;

для прямоугольника ( ): , ;

для треугольника ( ): , .

Координаты центра тяжести всей плоской фигуры вычисляются по формулам:

Задача 9. Определить положение центра тяжести круглой пластины радиуса с вырезом радиуса (рис. 31). Расстояние _.

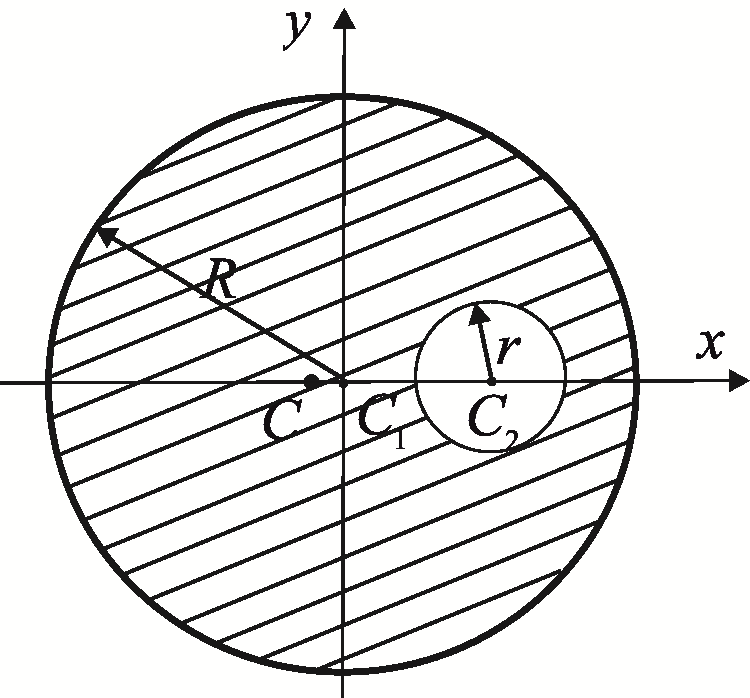
Рис. 31

Решение. Центр тяжести пластины лежит на линии , так как эта линия является осью симметрии. Проводим координатные оси. Для нахождения координаты дополняем площадь до полного круга ( ), а затем вычитаем из полученной площади площадь вырезанного круга ( ). При этом площадь , как вычитаемая, должна браться со знаком минус.

, , , , .

; .

Найденный центр тяжести как видим, лежит левее точки (рис. 31).