Лабораторная работа № 3

Решить симплекс-методом ЗЛП из лабораторной работы № 2.

2.3. Симплекс-метод с искусственным базисом

Вернемся к алгоритму симплекс-метода и заметим, что его применение возможно только при наличии начального базисного решения. Однако его можно получить, только если матрица А имеет вид . В этом случае ЗЛП представляется в виде

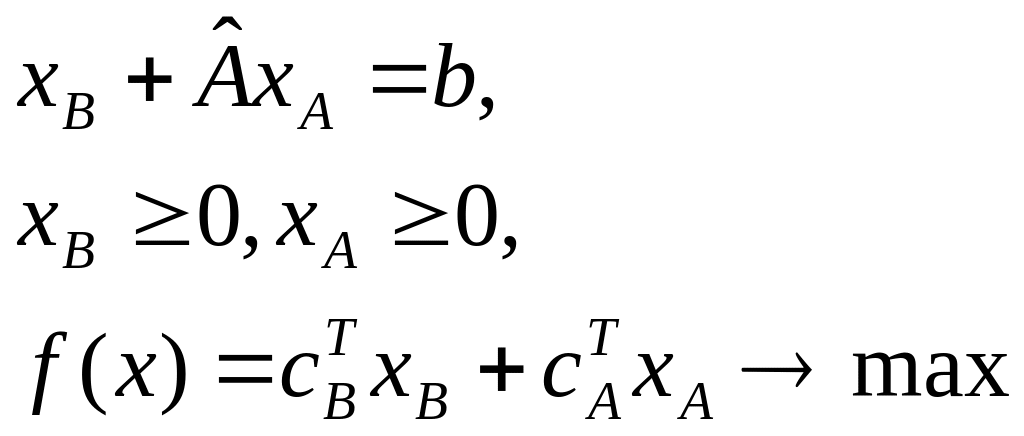
и имеется базисное решение с базисными компонентами .

Рассмотрим задачу.

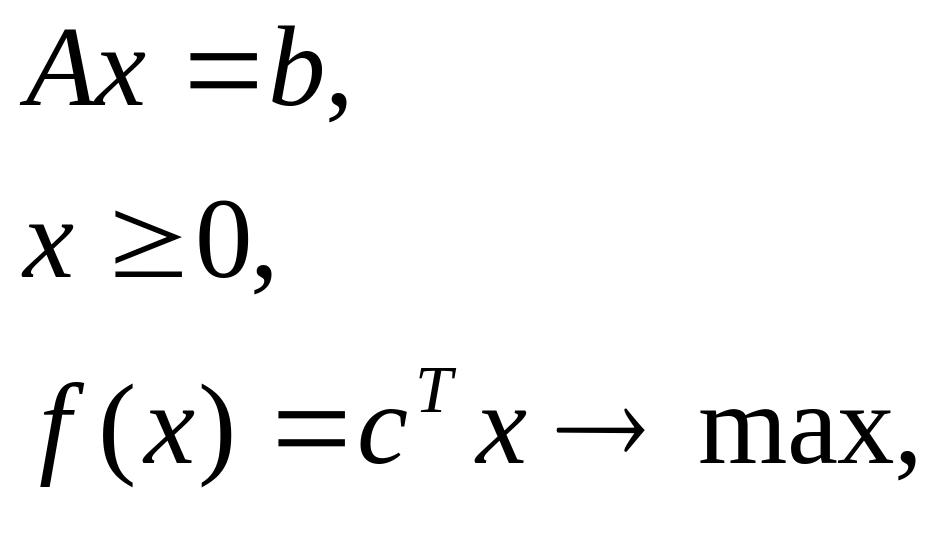(2.3.1)

где матрица А не имеет единичных столбцов или их число меньше числа строк матрицы.

В этом случае нет возможности найти начальное базисное решение, более того задача (2.3.1) может оказаться несовместной.

Поэтому задача решается в два этапа. На первом этапе отыскивается начальное базисное решение, а на втором – решается исходная задача с помощью алгоритма симплекс-метода.

Задача первого этапа:

,

, (2.3.2)

Переменные называются искусственными переменными.

Утверждение 1: Задача (2.3.2) разрешима.

Утверждение 2: Если при решении задачи (2.3.2) получено оптимальное решение и , то точка является допустимым решением задачи (2.3.1).

Утверждение 3: Если оптимальное значение целевой функции , то допустимое множество задачи (2.3.1) пусто.

На основе утверждений 1-3 и строится алгоритм симплекс-метода с искусственным базисом.

Алгоритм симплекс-метода с искусственным базисом

Шаг 0: Приведение к канонической форме.

Шаг 1: Запись всех исходных данных в таблицу.

Шаг 2: Просмотреть столбцы матрицы A и отыскать единичные столбцы с единицами в разных позициях. Соответствующие переменные занести в графу-базис.

Шаг 3: Просматривается базисный столбец, если он заполнен, то переход к алгоритму симплекс-метода.

Конец.

Иначе Этап 1.

Этап 1

Шаг 1: Свободные места в базисном столбце заполняются переменными с номерами соответствующими номерам строк.

Шаг 2: Целевые коэффициенты при переменных полагаются равными нулю ( ).

Целевые коэффициенты при полагаются равными минус единице.

Шаг 3: Переход к алгоритму симплекс-метода.

Шаг 4: Если , то выписывается ответ: Задача несовместна.

Конец.

Иначе переход к Этапу 2.

Этап 2

Шаг 1: Для всех переменных целевые коэффициенты полагаются равными .

Шаг 2: Переход к алгоритму симплекс-метода.

Конец.

Замечание 1: Единичные столбцы, соответствующие переменным , в таблицу не заносятся.

Пример 2.3. Решить задачу:

,

.

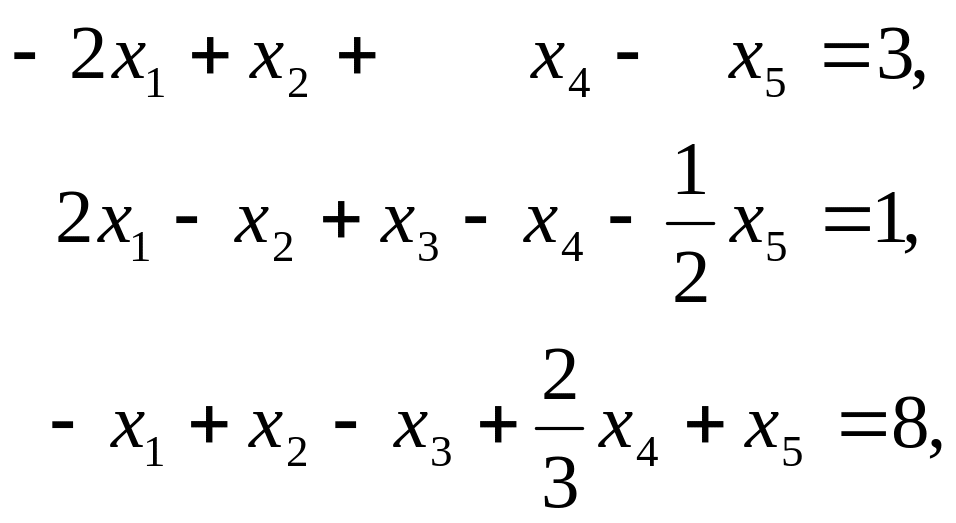
1.Занесём все данные задачи в табл. 2.3.

Таблица 2.3

B	cв	xв	1	-1	1	0	-3
		3	-2	1	0	1	-1
		1	2	-1	1	-1	-1⁄2
		8	-1	1	-1	2⁄3	1

2. Просматриваем табл. 2.3 и отыскиваем единичные столбцы для введения их в базис.

В таблице таких столбцов нет, поэтому в графу В заносят три искусственные переменные, а в графу c_в - коэффициент (-1) (табл. 2.4).

Таблица 2.4

B	cв	xв	0	0	0	0	0	Ө
z1	-1	3	-2	1	0	1	-1
z2	-1	1	2	-1	1	-1	-1⁄2
z3	-1	8	-1	1	-1	2⁄3	1

3. Вычисляем значения целевой функции по формуле . Вычисляем оценки по формуле (табл. 2.5).

Таблица 2.5

B	cв	xв	0	0	0	0	0	Ө
z1	-1	3	-2	1	0	1	-1
z2	-1	1	2	-1	1	-1	-1⁄2
z3	-1	8	-1	1	-1	2⁄3	1
		-12	1	-1	-1	-2⁄3	1⁄2

4. Так как ∆₄<0, то x₄ можно ввести в базис.

Вычисляем θ по формуле .

Минимальному значению θ будет соответствовать место направляющего элемента в столбце x₄.

Полностью все Шаги перестроения базисного решения представлены в табл. 2.6.

Таблица 2.6

B	cв	xв	0	0	0	0	0	Ө
z1	-1	3	-2	1	0	1	-1
z2	-1	1	2	-1	1	-1	-1⁄2
z3	-1	8	-1	1	-1	2⁄3	1
		-12	1	-1	-1	-2⁄3	1⁄2
Окончание табл. 2.6
B	cв	xв	0	0	0	0	0	Ө
x4	0	3	-2	1	0	1	-1	-
z2	-1	4	0	0	1	0	-3⁄2	-
z3	-1	6	1⁄3	1⁄3	-1	0	5⁄3	18
		-10	-1⁄3	-1⁄3	0	0	-1⁄6
x4	0	39	0	3	-6	1	9	-
z2	-1	4	0	0	1	0	-3⁄2	4
x1	0	18	1	1	-3	0	5	-
		-4	0	0	-1	0	3⁄2
x4	0	63	0	3	0	1	0
x3	0	4	0	0	1	0	-3⁄2
x1	0	30	1	1	0	0	1⁄2
		0	0	0	0	0	0

Так как все оценки и , то первый этап закончен и переходим ко второму этапу.

В верхнюю строку вновь заносим коэффициент и в столбец c_в - коэффициенты при базисных переменных (табл. 2.7).

Таблица 2.7

B	cв	xв	1	-1	1	0	-3
			А1	А2	А3	А4	А5
x4	0	63	0	3	0	1	0
x3	1	4	0	0	1	0	-3⁄2
x1	1	30	1	1	0	0	1⁄2
		34	0	2	0	0	2

Так как все оценки больше или равны нулю, следовательно, получено оптимальное решение:

,

.