5.2.3. Венгерский метод

Венгерский метод состоит из четырех этапов:

Этап 1. Приведение матрицы.

Этап 2. Подсчет – числа независимых нулей.

Этап 3. Преобразование матрицы С с целью получения новых нулей.

Этап 4. Поиск независимых нулей и получение оптимального решения.

Блок-схема последовательности выполнения этапов Венгерского метода приведена на рис. 5.2

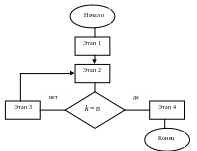
Рис.5.2. Блок-схема выполнения этапов Венгерского метода

Рассмотрим каждый этап подробно.

Этап 1. Приведение матрицы

Определение 2. Матрица С называется приведенной, если она имеет в каждой строке и в каждом столбце, по крайней мере, один ноль.

Матрица С легко приводится с помощью первого свойства, то есть вычитанием из строк и столбцов минимального элемента.

Алгоритм выполнения первого этапа

Шаг 0. .

Шаг 1. В каждой строке определяется .

Шаг 2. Для всех полагают .

Шаг 3. .

Шаг 4. Для каждого j полагают .

Шаг 5. Для всех полагают .

Шаг 6. .

Шаг 7. Переход ко второму этапу.

Этап 2. Подсчет k – числа независимых нулей

Пусть мы хотим вычеркнуть независимые нули горизонтальными или вертикальными линиями. Заметим, что никакие два независимых нуля нельзя вычеркнуть одной горизонтальной или вертикальной линией, так как они стоят в разных столбцах и строках. То есть если мы хотим вычеркнуть все независимые нули горизонтальными и (или) вертикальными линиями, то число этих линий будет совпадать с числом независимых нулей. Отсюда следует, что для того чтобы определить, сколько независимых нулей имеет матрица С, достаточно все нули матрицы С вычеркнуть минимально возможным числом горизонтальных и (или) вертикальных линий.

Рассмотрим следующую матрицу (рис. 5.3):

0	0	0	0
0
0
0

Рис. 5.3

Эта матрица является приведенной, так как в каждой строке и в каждом столбце имеется, по крайней мере, один ноль. При этом все нули могут быть вычеркнутыми двумя линиями: вертикальной и горизонтальной, - то есть эта матрица имеет всего два независимых нуля (рис. 5.4).

0	0	0	0
0
0
0

Рис. 5.4

Отсюда сформулируем алгоритм второго этапа.

Алгоритм выполнения второго этапа

Шаг 1. Отыскивается строка, содержащая один ноль. Этот ноль вычеркивается вертикальной линией. Процесс продолжается, пока может быть найдена строка, содержащая один ноль.

Шаг 2. Отыскивается столбец, содержащий один ноль. Этот ноль вычеркивается горизонтальной линией. Процесс продолжается, пока может быть найден столбец, содержащий один ноль.

Шаг 3. Просматриваются невычеркнутые элементы матрицы С.

Шаг 4. Если среди невычеркнутых имеются , то переход

к Шагу 7.

Иначе Шаг 5.

Шаг 5. Подсчитывается число линий k.

Шаг 6. Если , то переход к четвертому этапу. Если , то переход к третьему этапу.

Шаг 7. Просматриваются строки матрицы С и подсчитывается , где – число невычеркнутых нулей в i-й строке ( ).

Шаг 8. Просматриваются столбцы матрицы С и подсчитывается , где – число невычеркнутых нулей в j-м столбце.

Шаг 9. Если , то выбирается строка, содержащая нулей, и все нули вычеркиваются вертикальными линиями. Переход к Шагу 1.

Шаг 10. Если , то выбирается столбец, содержащий , невычеркнутых нулей и все нули вычеркиваются горизонтальными линиями. Переход к Шагу 2.

Замечание. В случае выхода на восьмой, девятый или десятые шаги, алгоритм, к сожалению, не гарантирует получение минимального числа линий, так как эти шаги являются эвристическими. Студенты могут попробовать предложить свои подходы к вычеркиванию нулей для случаев, когда их более одного в строке или столбце.

Этап 3. Преобразование матрицы С с целью получения новых нулей

Третий этап осуществляется, если полученное на втором этапе число независимых нулей недостаточно, поэтому необходимо преобразовать матрицу так, чтобы получить новые нули. Пометим через те элементы матрицы С, которые вычеркнуты одной линией, через - те элементы, которые вычеркнуты одновременно горизонтальной и вертикальной линиями, невычеркнутые элементы помечать не будем.

Алгоритм выполнения третьего этапа

Шаг 1. Найдем (из невычеркнутых ).

Шаг 2. Элементы матрицы С преобразуются по следующему правилу:

(для невычеркнутых),

(для вычеркнутых одной линией),

(для вычеркнутых одновременно двумя линиями).

Шаг 3. .

Шаг 4. Переход ко второму этапу.

Покажем, что приведенный алгоритм есть формализация преобразования матрицы с помощью ( ) шагов, основанных на первом свойстве матрицы С. Шаги 2-3 могут быть представлены следующим образом.

Шаг 2. Из всех строк вычисляется с, то есть .

Шаг 3. .

Шаг 4. Ко всем вычеркнутым строкам и столбцам прибавляется число с, то есть все вычеркнутые определяются по формуле .

Шаг 5. .

Отсюда получается, что после второго шага все элементы матрицы С уменьшаются на величину c. Следовательно, все нули становятся отрицательными числами, равными ( ), после четвертого шага все вычеркнутые элементы увеличиваются на с, при этом если элементы были вычеркнуты одной линией, то они не изменяются по сравнению с исходными значениями, а те элементы, которые были вычеркнуты горизонтальной и вертикальной линиями, одновременно увеличились на с, так как с один раз вычиталось и два раза прибавлялось. Именно эта процедура описана в алгоритме, но более кратко.

Этап 4. Поиск независимых нулей и получение оптимального решения

Алгоритм четвертого этапа подобен алгоритму второго этапа, однако имеет некоторые модификации.

Алгоритм выполнения четвертого этапа.

Шаг 1. В матрице размера ( ) помечаются места всех нулей.

Шаг 2. .

Шаг 3. Отыскивается строка, содержащая один ноль. Этот ноль выделяется, а соответствующие строка и столбец вычеркиваются. . (Процесс продолжается пока существует строка, содержащая один ноль.)

Шаг 4. Если , то переход к Шагу 11. Иначе Шаг 5.

Шаг 5. Отыскивается столбец, содержащий один ноль. Этот ноль выделяется, а соответствующие строка и столбец вычеркиваются. . (Процесс продолжается пока существует столбец, содержащий один ноль.)

Шаг 6. Если , то переход к Шагу 11. Иначе Шаг 7.

Шаг 7. Просматриваются строки и определяется – число невычеркнутых нулей в i-й строке.

Шаг 8. Просматриваются строки и определяется – число невычеркнутых нулей в j-м столбце.

Шаг 9. Если , то выбирается строка, содержащая нулей, один из нулей выделяется, а строка и столбец вычеркиваются. .

Переход к Шагу 3.

Шаг 10. Если , то выбирается столбец, содержащий нулей, один из нулей выделяется, а строка и столбец вычеркиваются. .

Переход к Шагу 3.

Шаг 11. На исходной матрице С помечаются элементы соответствующие помеченным нулям.

Шаг 12. Вычисляется целевая функция

.

Шаг 13. Сравнивается и S. Эти значения должны совпасть.

Пример 5.1 Дана матрица С (рис. 5.5). Решить задачу о назначениях.

3	6		8	10	15
	8	9	10	12	16
2		10	12	14	15
5	6	9	10	10
1	2	3		5	6
5	6	7	9		12

Рис. 5.5

Этап 1

Шаг 0. S=0.

Шаг 1 (рис. 5.6).

3	6		8	10	15	3
	8	9	10	12	16	4
2		10	12	14	15	2
5	6	9	10	10		5
1	2	3		5	6	1
5	6	7	9		12	5

Рис.5.6

Шаг 2. Из строк матрицы вычитаем соответствующее (рис. 5.7)

0	3	1	5	7	12
0	4	5	6	8	12
0	2	8	10	12	13
0	1	4	5	5	6
0	1	2	3	4	5
0	1	2	4	5	7

Рис. 5.7

Шаг 3. S=0+20=20.

Шаг 4 (рис. 5.8).

	0	3	1	5	7	12
	0	4	5	6	8	12
	0	2	8	10	12	13
	0	1	4	5	5	6
	0	1	2	3	4	5
	0	1	2	4	5	7
	0	1	1	3	4	5

Рис. 5.8

Шаг 5. Из каждого столбца вычитаем соответствующее (рис. 5.9).

0	2	0	2	3	7
0	3	4	3	4	7
0	1	7	7	8	6
0	0	3	2	1	1
0	0	1	0	0	0
0	0	1	1	1	2

Рис.5.9

Шаг 6. S=20+0+1+1+3+4+5=34.

Этап 2

Подсчет k – числа независимых нулей (рис. 5.10)

0	2	0	2	3	7
0	3	4	3	4	7
0	1	7	7	8	6
0	0	3	2	1	1
0	0	1	0	0	0
0	0	1	1	1	2

Рис. 5.10

переход к Этапу 3.

Этап 3

Шаг 1. с=1.

Шаг 2. Элементы матрицы С (рис. 5.110преобразуются по следующему правилу:

(для невычеркнутых),

(для вычеркнутых одной линией),

(для вычеркнутых одновременно двумя линиями).

0	2	0	1	2	6
0	3	4	2	3	6
0	1	7	6	7	5
0	0	3	1	0	0
1	1	2	0	0	0
0	0	1	0	0	1

Рис.5.11

Шаг 3. .

Переход к этапу 2.

Этап 2

Подсчет k – числа независимых нулей (рис. 5.112).

0	2	0	1	2	6
0	3	4	2	3	6
0	1	7	6	7	5
0	0	3	1	0	0
1	1	2	0	0	0
0	0	1	0	0	1

Рис.5.12

. Выбираем столбец. .

Переход к этапу 3.

Шаг 1. с=1.

Шаг 2. Аналогично предыдущей итерации (рис. 5.13).

0	1	0	0	1	5
0	2	4	1	2	5
0	0	7	5	6	4
1	0	4	1	0	0
2	1	3	0	0	0
1	0	2	0	0	1

Рис. 5.13

Шаг 3. .

Переход к этапу 2 (рис. 5.14).

0	1	0	0	1	5
0	2	4	1	2	5
0	0	7	5	6	4
1	0	4	1	0	0
2	1	3	0	0	0
1	0	2	0	0	1

Рис . 5.14

.

Переход к этапу 4 (рис. 5.15).

0			0
0
	0			0
				0	0
	0		0

Рис. 5.15

Переносим места выделенных нулей на исходную матрицу С. Получаем

.