
Учебное пособие 1942
.pdf
структивным и динамическим ограничениям /31/:
|
|
|
X (t) |
Q , |
X (t) |
Q , |
(3.3) |
|||
|
|
|
|
p |
|
X |
|
p |
X |
|
|
|
|
|
|
( X p (t), X p (t)) PF , |
|
(3.4) |
|||
|
|
|
|
|
|
|
|
|
|
|
где Q |
X |
, Q |
заданные ограниченные области в n-мерном пространстве; |
|
|
|||||
|
X |
|
|
|
|
|
|
|
||
PF — подпространство в 2n-мерном пространстве, вид которого определяется уравнением
движения |
|
|
|
|
, t t0 |
, |
(3.5) |
X (t) F[X (t), u(t), ξ], X (t0 ) X0 |
где X X(t) — n-мерный вектор состояний исполнительных приводов и механизмов в текущий момент времени t;
uu(t) — m-мерный вектор управлений;
—р-мерный вектор параметров двигательной системы; X 0 — начальное состояние.
Кроме того, ПД X p (t) должно удовлетворять заданным граничным условиям |
|
||||
|
X p (t0 ) |
X0 , |
X p (tТ ) |
X1. |
(3.6) |
Отметим также, что ПД X p (t) |
как частное решение уравнения движения (3.5) при неко- |
||||
тором допустимом управлении u |
up (t) зависит от |
параметров ξ |
Q . В задачах |
про- |
|
71

граммного управления предполагается, что эти параметры известны. В рассматриваемом случае на класс ПД накладываются более жесткие ограничения, связанные с учетом структуры множества QX состояний.
Построение ПД осуществляется с учетом свойств динамической модели робота с граничными условиями (3.6) и ограничениями (3.3) (3.4). Эффективным методом синтеза ПД является метод их параметризации с учетом граничных условий (3.6) /28, 29/. Этот метод обеспечивает отыскание приемлемых параметров ПД при выполнении граничных условий (3.6) и учете динамического ограничения (3.4), что достигается путем специального выбора базисных функций.
Рассмотрим подробно один из вариантов метода параметризации ПД /29, 30/. Будем искать ПД в многопараметрическом классе функций вида
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
X p (t) |
a0 (t) |
j a j (t), |
t [t0 , tT ] , |
(3.7) |
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
N |
|
|
|
|
|
где τ |
|
|
|
j 1 — вектор искомых параметров; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
a0 (t), a1 (t), ..., aN (t) — заданные N-мерные вектор-функции. |
|
|
|
||||||
Будем называть их базисными, если они удовлетворяют следующим условиям /28, 29/: |
|
||||||||
|
1) функции {a j (t)}Nj 0 |
таковы, что ПД (3.5) удовлетворяет граничным условиям (3.6) при |
|||||||
любом выборе параметров |
1, ..., N ; |
|
|
|
|
||||
|
2) функции {a j (t)}Nj 0 |
и их производные {a j (t)}Nj |
0 попарно удовлетворяют структурному |
||||||
ограничению (a j (t), a j (t)) |
PF при всех t [t0 , tT ] ; |
|
|
|
|
||||
72

3)функции {a j (t)}Nj 0 при любом конечном числе N линейно независимы;
4)каковы бы ни были функция X (t) на интервале [t0, tT] и положительное число , суще-
ствует натуральное число N и постоянные коэффициенты |
1, ..., |
N такие, что |
|
||
|
|
|
N |
|
|
|
|
|
|
|
|
|
X (t) |
a0 (t) |
τ j a j (t) |
ε ; |
(3.8) |
|
|
|
j 1 |
|
|
5) функции {a j (t)}Nj 0 достаточно просты для программной или схемной реализации.
Перечисленные требования к базисным функциям имеют следующий смысл. Первое требование обеспечивает решение двухточечной краевой задачи, второе гарантирует осуществимость параметризованного ПД (3.7) с учетом динамики робота, третье и четвертое означают возможность экономного и вместе с тем сколь угодно точного представления ПД в виде (3.7) и, наконец, пятое обеспечивает простоту технической реализации искомого ПД.
Первая задача в рамках параметрического метода построения ПД заключается в рациональном выборе базисных функций. Рассмотрим некоторые примеры и общие рекомендации по конструированию базисных функций.
Базисными функциями, удовлетворяющими сформулированным требованиям, могут служить полиномы
a0 (t) |
X 0 ( X1 |
|
|
X 0 )T |
1 (t t0 ), |
||
|
|
|
|
|
|
) j (t |
(3.9) |
a (t) |
a |
0 |
(t)(t |
t |
0 |
t), |
|
j =1, …,j N. |
|
|
|
T |
|
||
73
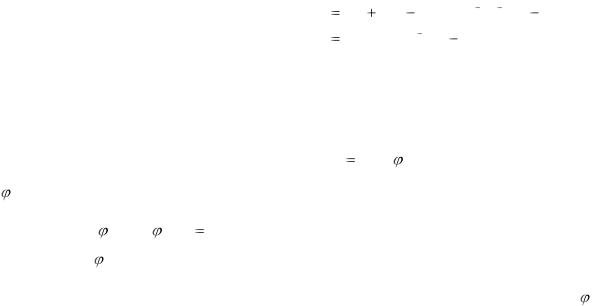
В самом деле, при таком выборе базисных функций ПД (3.7) удовлетворяет граничным условиям (3.6), динамическому ограничению (3.4), а также требованиям точной аппроксимации и простой реализации.
Другим примером рационального выбора базисных функций являются тригонометрические многочлены
a0 (t) |
X 0 ( X1 |
X 0 ) sin 2 1T |
1π(t t0 ), |
a j (t) |
a0 (t) sin jT |
1π(t t0 ). |
(3.10) |
|
При конструировании базисных функций можно руководствоваться следующим правилом: в качестве функции a0 (t) выбирать непрерывно дифференцируемую вектор-функцию,
удовлетворяющую граничным условиям (3.6), а в качестве остальных базисных функций - функции вида
a j (t) a0 (t) j (t), j =1, …, N, |
(3.11) |
где j (t ) — числовые функции на временном интервале [t0, tT], удовлетворяющие однородным граничным условиям, т. е.
j (t0 ) 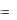 j (tT ) 0, j =1, …, N. (3.12)
j (tT ) 0, j =1, …, N. (3.12)
В качестве j (t) можно выбирать рассмотренные полиномы и тригонометрические многочлены.
Большой интерес представляет также такая параметризация ПД, когда в качестве j (t) бе-
74
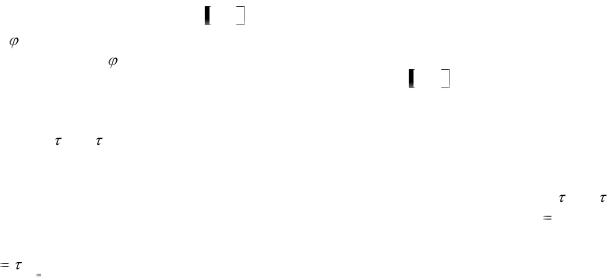
рутся сплайны /15, 23/, т. е. кусочно-полиномиальные функции со следующими свойствами:
1) существует разбиение t0 , tT на подынтервалы, такое, что внутри каждого подынтерва-
ла j (t) представляет собой многочлен степени r ;
2) функции j (t) непрерывны вместе с производными до (r-1)-го порядка и имеют интегрируемую с квадратом производную порядка r на интервале t0 , tT .
Конструирование базисных функций с учетом высказанных соображений обеспечивает соблюдение граничных условий (3.6), динамического ограничения (3.4) при любом выборе параметров 1, ..., N в функции (3.7), а также приводит к высокой точности аппроксимации и простой реализации синтезируемых ПД. После выбора базисных функций a0 (t), a1(t), ...,aN (t) можно перейти к фактическому построению ПД вида (3.7).
Задача синтеза ПД сводится к отысканию приемлемых значений параметров |
1, ..., N. Эти |
|||
параметры следует определять исходя из заданных ограничений (3.3), где |
Q |
F (Q |
X |
, Q , ξ ) . |
|
X |
|
U |
|
Ограничения (3.3) с учетом (3.7) превращаются в систему неравенств относительно параметров
τ |
|
j |
|
N . |
|
|
|||
|
|
|
j 1 |
|
|
|
|
|
Таким образом, задача построения ПД в результате параметризации (3.7) сводится к решению системы неравенств, описывающих ограничения (3.3), относительно параметров искомого ПД.
Для решения полученных неравенств простым и эффективным является метод, использующий рекуррентные конечно-сходящиеся алгоритмы /39/ решения неравенств.
3.3. Конечно-сходящиеся алгоритмы решения
75

рекуррентных неравенств
Введем искомый вектор подстраиваемых параметров . Пусть t = 0, 1, ... , t-1 - дискретное
время; t ( ), t ( |
)- вещественные функции. Предположим, что имеется правило, |
сопостав- |
|||
ляющее каждому набору τ0t-1 векторов [ 0, 1, ..., |
t-1], составляющие которого соответствуют |
||||
значениям вектора |
в дискретные моменты времени, две функции от |
: |
|
|
|
|
t (t) |
t (τ, τ0t 1 ), |
t (t) |
t (τ, τ0t 1 ). |
(3.13) |
(Далее, для краткости, аргументы τ t -1 у этих функций не выписываются). |
|
||||
|
0 |
|
|
|
|
|
1. Рассмотрим неравенства |
|
|
||
|
|
t (τ ) 0 |
( 0), |
|
(3.14) |
которые будем называть условными неравенствами, и неравенства |
|
|
|
||
|
|
t (τ ) 0 |
( |
0), |
(3.15) |
которые будем называть безусловными неравенствами.
В задачах адаптивного управления неравенства (3.14) порождаются целевым условием (целью управления); неравенства (3.15) описывают ограничения на возможные значения вектора τt подстраиваемых параметров. Знаки или > в (3.14), (3.15) в каждый момент времени мо-
гут быть любыми. Неравенства (3.15) в частном случае могут отсутствовать.
76

Пусть заданы множество |
{ }° начальных значений вектора |
0 |
подстраиваемых парамет- |
|||||||||||
ров и правило |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
t 1 |
|
T (τ |
t , |
t , |
t |
), |
t 1,2, ..., |
(3.16) |
|
|
|
|
|
|
|
t |
0 |
0 |
0 |
|
|
|
|
сопоставляющее набору τ0t |
и наборам функций |
|
|
|
|
|
|
|
|
|
||||
|
|
t |
{ |
0 (τ ), ..., |
t (τ )}, |
|
t |
{ |
0 (τ ), ..., |
t (τ )} |
|
|||
|
|
0 |
|
0 |
|
|||||||||
значение |
τt 1 . Тогда |
для |
заданных |
τ {τ}0 , |
0 (τ), |
0 (τ) |
последовательно |
определяются |
||||||
τ1, 1 (τ), |
1 (τ), τ2 , 2 (τ), |
2 (τ), |
и т. д. Неравенства (3.14), (3.15) заранее для всех t не заданы, |
|||||||||||
они появляются последовательно во времени после очередного «срабатывания» алгоритма (3.16). Поэтому будем называть (3.14) и (3.15) рекуррентными неравенствами. Для разных алгоритмов (3.16) неравенства (3.14) и (3.15) будут разными. Правая часть (3.16) обычно зависит лишь от τt , t , t .
Уравнение (3.16) является конечно-сходящимся алгоритмом (КСА) решения рекуррентных неравенств - условных (3.14) и безусловных (3.15), если для всех t выполнено (3.15) при
τ τt и если существует такой момент времени t* , |
что для t t* выполняются неравенства |
(3.14) при τ τt и векторы t далее не изменяются: τt* |
τt* 1 ... . Число r моментов времени t |
1, для которых при τ τt не выполняется (3.14), называется числом ошибок (коррекций) алгоритма.
77
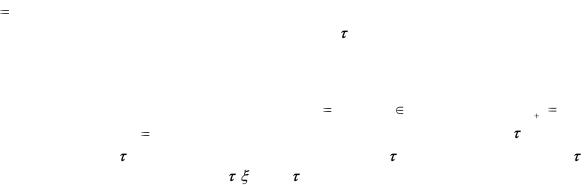
Итак, КСА - алгоритм, доставляющий решение бесконечного числа заранее незаданных условных рекуррентных неравенств: неравенства (3.14) при t < t* могут остаться невыполненными. На каждом шаге решение должно выбираться из области, определяемой также появляющимся рекуррентным неравенством.
Важно помнить, что рекуррентные неравенства (3.14), (3.15) могут зависеть от алгоритма (3.16): для разных алгоритмов они разные.
При решении задачи построения КСА требуется за конечное время найти решение бесконечной системы неравенств, заранее неизвестных. Однако, многие задачи адаптации приводят к рекуррентным неравенствам, для которых выполнен ряд дополнительных свойств, что дает возможность строить такие алгоритмы. Наличие определенной стабильности, присущей обычно практическим задачам, приводит к тому, что неравенства (3.14), (3.15) выполняются для всех t при значениях подставляемых параметров из некоторой окрестности вектора τ(ξ). Иначе,
для τ τ(ξ) эти неравенства выполнены «с запасом». Второе важное свойство, которое часто
имеет место, - это наличие областей в пространстве { }, определяемых рекуррентными неравенствами (3.14), (3.15). Указанные два обстоятельства позволяют строить КСА следующим образом.
Пусть безусловные неравенства отсутствуют. Обозначим через Тt область, определяемую
неравенством (3.16). Если (3.14) выполняется для τ τt , т.е. τ |
Тt , то полагаем τt 1 τt . Если |
|
(3.14) не выполнено для τ |
τt , то существует плоскость Пt, отделяющая вектор t от множества |
|
Тt. Выберем в качестве t +1 |
ортогональную проекцию вектора |
t на плоскость Пt. Вектор t+1 бу- |
дет ближе к неизвестному нам вектору ( ), чем t. Из сделанных предположений следует суще-
78
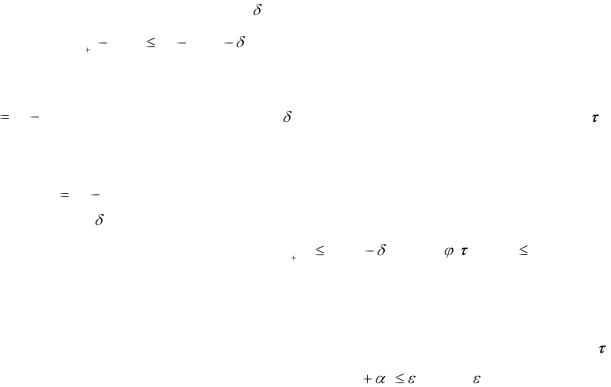
ствование такого не зависящего от t числа |
> 0, что |
|
|
|
||||||||||||||
|
|
|
|
|
τt 1 |
τ(ξ) |
|
2 |
|
τt τ(ξ) |
|
2 |
. |
(3.17) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||
Итак, построенный алгоритм будет обладать свойством (3.17). Отсюда следует его конеч- |
||||||||||||||||||
ная сходимость. Каждый раз, когда не выполнено (3.14), справедливо (3.17), т. е. величина |
|
|||||||||||||||||
V (τt ) |
|
τt τ(ξ) |
|
2 |
убывает по меньшей мере на . Когда неравенство (3.14) выполнено, то V( t) |
|||||||||||||
|
|
|||||||||||||||||
не изменяется. Поэтому число r ошибок алгоритма конечно. |
|
|
||||||||||||||||
Плоскость Пt |
можно строить по-разному: при этом получаются различные КСА. Вместо |
|||||||||||||||||
|
|
τ(ξ) |
|
2 можно выбрать любую неотрицательную функцию; важно лишь, что- |
||||||||||||||
функции V(τt ) |
τ |
|
||||||||||||||||
бы для некоторого |
> 0 выполнялось |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V (τt 1 ) |
V (τt ) |
при ( ) <0 ( 0). |
(3.18) |
Рассмотрим КСА «Полоска-1», который целесообразно использовать при прямоугольной форме препятствий.
3.4. Конечно-сходящийся алгоритм «Полоска-1»
Рассмотрим следующую систему условных рекуррентных неравенств в пространстве { }:
(at , τ ) |
t |
t |
(< t ) , |
(3.19) |
79

где t = 0, 1, 2, ...; at |
{ }; |
|
|
(аt , |
) — скалярное произведение векторов аt и |
; |
|
t , |
t — вещественные числа. |
|
|
Запись (< t ) в (3.19) означает, что вместо | . . . | |
t для некоторых t (в частности, для всех |
||
t) может быть |. . . |< |
t . Относящиеся к этому случаю изменения также будут записаны в скобках |
||
(...). |
|
|
|
Неравенство (3.19) для фиксированного t определяет полосу между двумя параллельными плоскостями в пространстве { }. Полосы (3.19) по смыслу решаемой задачи могут быть заранее
неизвестны: предполагается заданным некоторый алгоритм, |
доставляющий по значениям 0, |
||||||||
..., t вектор at { } и числа |
t , t . |
|
|
|
|
|
|
|
|
Будем предполагать выполненными следующие условия: |
|
|
|
|
|
|
|||
а) существует такое |
> 0, что для любого t 0 |
|
|
|
|
|
|
||
|
|
|
t |
|
at |
|
, |
(3.20) |
|
|
|
|
|
|
|||||
б) существуют вектор |
* и число (0 |
< 1), такие, что при всех t |
0 выполняется нера- |
||||||
венство |
|
|
|
|
|
|
|
|
|
|
|
|
(at , τ*) |
|
t |
|
|
t . |
(3.21) |
|
|
|
|
|
|
||||
Пусть выполняются условия а) и б). Введем обозначение:
80
