
Учебное пособие 1942
.pdfРешение прямых и обратных задач о положении и скорости используется при формировании кинематических алгоритмов управления манипулятором.
2.5. Кинематические алгоритмы управления
Кинематические алгоритмы строятся по кинематическим уравнениям. Различают кинематические алгоритмы нулевого и первого порядка, если в качестве управляющих параметров используются соответственно кинематические переменные и их скорости изменения (первые производные по времени).
Рассмотрим особенности этих алгоритмов. Кинематический алгоритм нулевого порядка основан на реализации соотношения
qзад = F -1(Xзад), |
(2.37) |
где qзад – вектор заданных значений обобщенных координат манипулятора; Xзад – вектор заданных значений декартовых координат рабочего органа.
Уравнение (2.37) решает обратную задачу кинематики о положении, т.е. по координатам целевой точки в базовой системе отсчета определяет вектор обобщенных координат, который поступает на входы приводных систем робота в качестве задающих воздействий. Предполагается при этом, что алгоритмы приводной системы синтезированы, приводы замкнуты по положению, т.е. по координатам qs, s =1, 2, 3,..., n.
Особенность управления состоит в том, что оно осуществляется по разомкнутой схеме, текущее состояние ИМ в процессе его движения не учитывается при формировании управляющих воздействий на приводы. Структурная схема, отвечающая рассмотренному алгоритму,
61
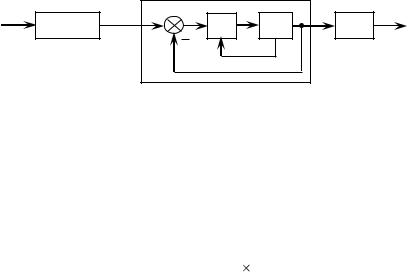
приведена на рис. 2.2.
Хзад |
F-1(Xзад) |
ПС |
ИМ |
q |
1. |
|
F(q) |
||||
|
qзад |
|
|
|
|
|
q |
q |
|
|
|
Рис.2.2. Структурная схема системы, управляемой |
по положению |
На рис.2.2 приняты обозначения: |
|
ПС — приводная система; ИМ — исполнительный механизм.
Практическое применение алгоритмов нулевого порядка ограничено теми ситуациями, когда допустимо программное управление без обратных связей.
Кинематический алгоритм первого порядка использует решение обратной задачи кинема-
тики для скоростей |
|
|
. |
. |
|
qзад(t) = J- 1 [q(t )] |
Xзад(t), |
(2.38) |
где q зад(t) – вектор заданных значений скоростей обобщенных координат манипулятора;
X зад(t) – вектор заданных значений скоростей декартовых координат рабочего органа. Вектор X(t) текущих базовых координат вычисляются по уравнению (2.1) и вектору q(t)
измеренных значений скоростей обобщенных координат. При сравнении векторов Xзад(t) и X(t)
62
получается вектор X зад(t) корректирующих внешних скоростей, используемый для того, чтобы уменьшить ошибку позиционирования. Вектор q зад(t) требуемых скоростей сочленений вы-
числяется из (2.38). Приводные системы, замкнутые по положению, отрабатывают командные значения обобщенных координат qзад(t), вычисленные путем интегрирования заданных скоростей q зад(t). Возможна и другая схема управления, в которой приводы, управляемые по скоро-
сти, непосредственно отрабатывают сигналы q зад(t).
Рассмотренный способ управления называется управлением по вектору скорости. Данный способ реализуется во множестве вариантов, отличающихся алгоритмами формирования векто-
ра Х зад(t) по результату сравнения заданного Xзад(t) и фактического X(t) перемещений рабочего органа, способами решения уравнения (2.38), а также связи с конкретными приводными системами. Информацию об управлении по вектору скорости можно получить из /23/.
Рассмотрим один из вариантов синтеза управления по вектору скорости для ТМ, приводные системы которого замкнуты по положению.
Задачу сформулируем следующим образом. В начальный момент t = 0 положение контро-
лируемой точки ИМ характеризуется значениями |
|
|
. |
. |
|
xs(0) = xs0, xs(0) = xs0, s = 1, 2, 3. |
(2.39) |
|
Требуется осуществить движение, при котором контролируемая точка ИМ перемещается
в окрестность неподвижной точки Xзад=(xзад1, xзад2, xзад3)т. При этом процесс xs(t) xзадs должен
соответствовать решению дифференциальных уравнений:
.. .
63

xsэ(t) + K1s xsэ(t) + K0s xsэ(t) = K0s xзадs, |
s = 1, 2, 3. |
(2.40) |
|
Эталонный процесс xsэ(t) xзадs реализуется в том случае, когда ускорение |
|||
|
.. |
. |
|
|
xsэ(t)=K0s(xзадs-xsэ(t))-K1sxsэ(t), |
(2.41) |
|
поэтому будем определять требуемое ускорение из уравнения |
|||
.. |
. |
. |
|
xsэ(t) = asэ(xs, xs) = K0s(xзадs-xs(t))-K1sxs(t), |
(2.42) |
||
После интегрирования выражения (2.42) получим уравнение для определения требуемой скорости:
Vsэ = K0s
В векторной форме ниями:
.
t |
|
(xзадs-xs(t))dt - K1s xs (t). |
(2.43) |
0 |
|
управление по вектору скорости описывается следующими уравне-
t
Vэ(t) = K0 (Xзад - X)dt - K1X, |
|
0 |
|
qэ(t) = J -1(q) Vэ(t), |
(2.44) |
t . |
|
qэ(t) = qэ(t)dt,
0
64
где К0 = diag{K0s}, K1 = diag{K1s}.
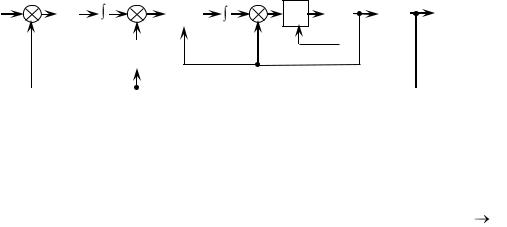
Структурная схема системы, управляемой по вектору скорости, представлена на рис. 2.3. В том случае, если приводные системы замкнуты по скорости, на них поступает вектор
qэ без |
|
|
|
|
|
|
|
|
|
дополнительного |
|
|
интегрирования. |
||||||||||||
Хзад |
К0 |
|
|
|
Vэ |
J-1(q) qэ |
|
qэ |
|
ПС ИМ q |
F(q) 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
q |
|
q |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
K1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.3. Структурная схема системы, управляемой по вектору скорости
Необходимо отметить, что равенство X(t)=Xэ(t) точно реализуется только в идеальном случае, когда требуемое значение qэ(t) (или qэ (t) ) отрабатываются мгновенно, т.е. когда систе-
ма приводов и ИМ безынерционны. Чтобы эталонный процесс xsэ(t) xзадs был физически реализуем, числовые значения K0s, K1s необходимо назначать с учетом динамики приводной системы и ИМ.
Пусть динамика контуров управления по каждой степени подвижности аппроксимируется
65
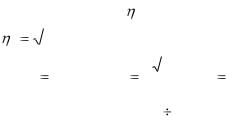
дифференциальными уравнениями |
|
|
|||||||||||
|
|
|
|
|
|
.. |
. |
|
|
|
|
||
|
|
|
|
Тs2qs + 2 |
s qs + qs = qзадs. |
(2.45) |
|||||||
При |
|
|
|
расчет параметров рекомендуется выполнять по формулам /12/ |
|||||||||
s |
2 / 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K0s |
|
|
1 |
|
|
, K1s |
2 |
|
, s 1, 2, 3, |
(2.46) |
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
2 |
|
|
|
|
||||
|
|
|
N |
T |
|
|
|
N T |
|
|
|||
|
|
|
|
s |
s |
|
s s |
|
|
||||
где Ns = 5 6.
66

3. ПЛАНИРОВАНИЕ ДВИЖЕНИЙ ПРОМЫШЛЕННОГО РОБОТА
3.1. Общие вопросы планирования движений робота
Выполнение манипуляционным роботом даже самой простой операции требует планирования траектории движения схвата в пространстве и во времени. Если операция задается роботу в обобщенном виде, то планирование выполняется автоматически с помощью некоторого алгоритма на цифровой вычислительной машине.
Перед началом движения манипулятора необходимо знать, во-первых, существуют ли на его пути какие-либо препятствия, и во-вторых, накладываются ли ограничения на траекторию схвата. В зависимости от ответов на эти два вопроса закон управления манипулятором принадлежит к одному из четырех типов, указанных в табл. 3.1.
Таблица 3.1
Типы управления манипулятором
Препятствия |
Препятствия на пути манипулятора |
|
|
||
Ограничения |
Присутствуют |
Отсутствуют |
67

Ограничения на траекторию манипуля-
тора
|
Автономное плани- |
Автономное плани- |
||
|
рование |
траектории, |
рование |
траектории |
Присут- |
обеспечивающее об- |
плюс регулирование |
||
ствуют |
ход |
препятствий, |
движения |
вдоль вы- |
|
плюс регулирование |
бранной траектории в |
||
|
движения вдоль вы- |
процессе |
движения |
|
|
бранной траектории |
манипулятора |
||
|
в процессе движения |
|
|
|
|
|
|
||
Отсут- |
Позиционное управ- |
Позиционное |
||
ствуют |
ление плюс обнару- |
управление |
||
|
жение и обход пре- |
|
|
|
|
пятствий в процессе |
|
|
|
|
движения |
|
|
|
|
|
|
|
|
Как видно из табл. 3.1, наиболее сложной задачей является автономное планирование траектории, обеспечивающее обход препятствий. Создание автономно функционирующих роботов связано с роботизацией технологических процессов и потребностями космической и подводной техники. Рассмотрим методы построения программных траекторий на примере подвижного робота.
Предполагается, что внешняя среда содержит запрещенные области, играющие роль препятствий для подвижного робота. В процессе движения робот должен обходить эти препятствия, выполняя при этом определенные задания — целевые условия.
68
Целевые условия могут задаваться роботу в обобщенном виде: «передвинуться в заданный район», «взять определенный объект и погрузить его на тележку», «выполнить заданную последовательность технологических операций» и т.п. Система управления автоматически строит программные движения (ПД) тележки и манипулятора, соответствующие заданным целевым условиям, которые затем отрабатываются на исполнительном уровне управления.
При построении закона изменения обобщенных координат, обеспечивающего выполнение на интервале движения некоторого целевого условия, необходимо удовлетворить следующим требованиям:
1.В процессе движения все звенья манипулятора и тележки не задевают препятствий.
2.Выполнены конструктивные ограничения на обобщенные координаты.
3.Движения манипулятора и тележки достаточно плавные.
Условие плавности движений манипулятора определяет ограничения на скорости и ускорения координат в пределах от минимального до максимального значений:
. |
. |
. |
.. |
.. .. |
|
qjmin< qj < qjmax, |
qjmin< qj < qjmax, j= 1 4. |
(3.1) |
|||
По конструктивным соображениям ограничены перемещения звеньев манипулятора:
qjmin< qj < qjmax. |
(3.2) |
Имеются также ограничения, связанные с препятствиями.
Система линейных неравенств, порожденных препятствиями, а также неравенств, обусловленных конструктивными ограничениями, разрешима, если целевые условия вообще вы-
69

полнимы в рассматриваемом классе движений. Для решения системы неравенств применяют метод конечно-сходящихся алгоритмов /34/.
Траектория движения робота может быть спланирована непосредственно в системе обобщенных координат манипулятора, а также в системе декартовых координат в виде последовательности узловых точек, через которые должен пройти схват в процессе перемещения из начального положения в конечное. Во втором случае решается обратная задача о положении механизма для каждой узловой точки (см. п. 2.1 2.4), в результате чего получается матрица значений обобщенных координат, каждый столбец которой определяет конфигурацию механизма в системе обобщенных координат для определенной узловой точки. Полученные значения обобщенных координат в узловых точках являются сигналами для исполнительного уровня управления.
Планирование движений не заканчивается построением матрицы дискретных значений обобщенных координат. Далее необходимо решить задачу определения продолжительности управления и разбиения этого интервала на необходимое число отрезков, а также задачу интерполяции, т.е. задачу определения задающих сигналов для любого текущего момента времени.
Рассмотрим теоретические вопросы планирования движений промышленного робота с учетом препятствий, а также интерполяции с помощью сплайн-функций.
3.2. Теоретический подход к построению |
программных движений робо- |
та |
|
Программное движение X p (t) при всех t |
[t0 , tT ] должно удовлетворять следующим кон- |
70
