
Учебное пособие 1878
.pdf
2.1.4. Свойства плана ускорений
1–3. Эти свойствааналогичны свойствам планаскоростей.
4.Угловую скорость второго звена можно определить:
2 aCB .
CB
2.1.5. Построение плана скоростей и ускорений кулисного механизма (рис. 2.5)
|
|
D |
4 |
|
|
|
|
5 |
|
|
|
|
E |
|
|
1 |
|
2 |
|
|
|
B |
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
C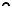
Рис. 2.5
Дано: 1 = const, размеры звеньев.
Определить скорости и ускорения всех точек механизма. Механизм содержит подвижных звеньев n=5; кинематических пар 5-го класса P5=7; степень подвижности W=1, класс
механизма – 2 (рис. 2.6).
ТочкаВ1 совершаетвращательноедвижениевокруг точки А
VB1= 1 AB ;
точка В3 совершает вращательное движение вокруг точки С; точка В2 совершает сложное движение – переносное враща-
31

тельное вместе с точкой В3 и относительное поступательное вдоль звена СД:
|
VB |
2 |
VB |
3 |
VB |
B |
; |
VB |
2 |
VB . |
|
|
|
|
2 |
|
3 |
|
1 |
|
|||
|
2 |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 |
B3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
1 |
B1 |
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
||
А |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C
Рис. 2.6. Структура кулисного механизма Построим план скоростей (рис. 2.7).
P e
e
b3  d
d
b12
Рис. 2.7
Скорость точки D находим исходя из свойства подобия:
CD |
|
Pd3 |
; Pd3 |
Pb3 CD |
; Vd3 Vd |
4 . |
|
|
|
||||
CB Pb3 |
CB |
|
||||
32
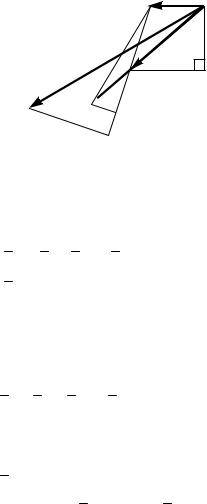
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VD |
VE D |
; |
|||||
VE |
5 |
|||||||||
|
|
|
3 |
5 |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VE0 |
VE5E0 ; . |
||||||
VE5 |
||||||||||
|
|
|
|
0. |
|
|
|
|
||
|
|
|
|
|
|
|
||||
V |
|
|
|
|
|
|||||
|
E0 |
|
|
|
|
|
|
|
||
Переходим к плану ускорений (рис. 2.8).
e |
|
b3 |
|
d
b12
Рис. 2.8
|
an |
|
|
2 |
|
AB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
B |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
aB3 |
aB12 |
aB12B3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
aB12B3 звено3; |
|||||||||||||||||||||||||||||||||||||
|
a |
B3 |
|
a |
C |
|
a |
n |
|
|
a |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B3C |
|
|
|
|
|
|
B3C |
|
|
||||||||||||||
|
a |
k |
|
B |
|
2 |
3 |
|
V |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B B |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
12 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
|
an |
|
|
VB2C |
|
|
|
Pb |
|
|
V |
2 |
; |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
B |
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
BC |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
aE aD aED aED |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
a |
|
|
|
a |
|
|
|
|
a |
k |
|
|
a |
r |
|
|
звенья4,5; |
||||||||||||||||||||||
E |
E0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
EE0 |
|
|
|
|
|
|
EE0 |
|
|
|
|
||||||||||||||||
aEDn |
VED2 |
|
|
ed V 2 ; |
|
|
|
|
|||||||||||||||||||||||||||||||
ED |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ED |
|
|
|
|
|
|
|
|||||||||||||
a |
k |
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
EE0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
an |
|
||ED; |
|
|
|
|
|
a |
|
|
|
|
ED; |
|
a |
r |
||xx. |
||||||||||||||||||||||
|
|
ED |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ED |
|
|
|
|
|
|
|
|
|
|
|
|
EE0 |
|||||||
33
2.2. Силовой анализ механизмов
Силовой анализ механизмов представляет собой решение первой задачи динамики системы: определение сил по заданному закону движения. Определению подлежат реакции в кинематических парах механизма. Для решения этой задачи применяется метод кинетостатики, формальный прием, который позволяет записать уравнения движения в форме уравнений равновесия и, следовательно, решать задачу методами статики.
Заметим, что метод кинетостатики это не единственный способ решения этой задачи: можно, освобождаясь от связей, вводить реакции связей в уравнение движения системы и находить последние из них. Звенья механизма, находящегося в движении, в общем случае не находятся в равновесии, т.к. они движутся с ускорениями.
Однако мы можем рассматривать равновесие всего механизма и каждого звена в отдельности, если применим к решению этой задачи принцип Даламбера, который утверждает следующее: если систему, находящуюся в движении, в какой – либо момент времени мгновенно остановить и к каждой материальной точке этой системы приложить действовавшие на нее в момент остановки активные силы, реакции связей и силы инерции, то система останется в равновесии.
При определении неизвестных реакций мы будем расчленять механизм, пользуясь принципом освобождаемости от связей, т.е. будем выделять из механизма группы звеньев и отдельные звенья, рассматривать их равновесие. При этом воздействие отброшенных звеньев представим реакциями, действующими на рассматриваемые звенья в расчлененных кинематическихпарах.
2.2.1. Условие статической определимости кинематических цепей
Расчленяя механизм на структурные группы и прикладывая в расчлененных кинематических парах реакции со стороны отброшенных звеньев, следует иметь в виду, что не всякая выделенная из механизма кинематическая цепь будет статически
34
определимой. Статически определимой называется система, в которой число неизвестных (определяемых сил) будет равно числу уравнений статики. Для плоских механизмов, в состав которых входят кинематические пары 5-го и высшие пары 4-го классов, и на которые действует плоская система сил, число неизвестных реакций связей совпадает с числом ограничений, имеющихся в этих кинематических парах. Так, например, соединение звеньев во вращательную кинематическую пару 5-го класса отнимает возможность движения центра вращения вдоль координатных осей за счет возникновения сил, препятствующих движению в этих направлениях.
Таким образом, определению подлежат обе проекции силы реакции на координатные оси, т.е. неизвестных будет два. Если же говорить о равнодействующей силе реакции как о векторе, то неизвестными будут величина и направление силы. Третья характеристика силы – точка ее приложения – может быть условно помещена в центр шарнира (поскольку сила
– это скользящий вектор). Конечно, «точка приложения» это понятие условное, так как силы реакции распределены по поверхности соприкосновения звеньев, однако равнодействующая реакции проходит через центр шарнира (рис. 2.9).
_ |
2 |
|
R12 |
||
|
1
Рис. 2.9
Соединение звеньев в поступательную пару 5-го класса отнимает свободу движения вдоль одной из координатных осей (этому движении препятствует сила, направленная вдаль этой оси) и свободувращения вокруг оси, перпендикулярной координатной плоскости. Это говорит о том, что реакция создает мо-
35
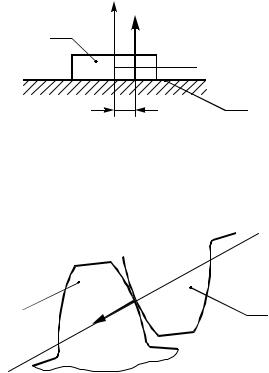
мент, направленный против момента активных сил. Таким образом, в этой кинематической паре также имеются две неизвестные характеристики силы: величина и точка ее приложения. Обычно начало координат помещается в центр смежной вращательной кинематической пары, относительно оси которой могло бы совершаться вращение рассматриваемого звена (рис. 2.10).
y |
_ |
2 |
R12 |
 x
x
a 1
Рис. 2.10
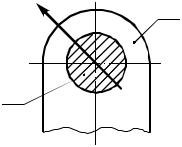
В высшей паре четвертого класса неизвестна только одна характеристика силы: ее величина, т.к. направление её (по нормали к соприкасающимся поверхностям звеньев) и точка приложения известны (рис. 2.11).
 N
N
|
_ |
|
2 |
R12 |
1 |
|
|
N
Рис. 2.11
Таким образом, если в выделенную из механизма кинематическую цепь будет входить n звеньев, то для них можно составить 3n уравнений статики ( x=0, y=0, z=0). Число неизвестных в этих уравнениях будет соответствовать удвоенному числу кинематических пар 5-го класса плюс число кинематических пар 4-го класса, т.е. общее число неизвестных в выделенной кинематической цепи будет равно 2Р5+Р4. Для
36
того чтобы кинематическая цепь была статически определимой, число уравнений должно быть равно числу неизвестных, т.е. должно удовлетворяться условие
3n=2Р5+Р4.
Этому условию удовлетворяют группы Ассура. Вот почему для определения реакций механизм расчленяется на них.
2.2.2. Силы, действующие на звенья механизма
Применение метода кинетостатики предполагает использование принципа Даламбера, в связи с чем необходимо определять силы инерции звеньев механизма.
Сила инерции не является сосредоточенной силой: она распределена по всему объему звена, которое может рассматриваться как тело, состоящее из бесконечно большого числа элементарных масс, при движении которых возникают элементарные силы инерции. Для упрощения расчетов систему элементарных сил инерции приводят к главному вектору и главному моменту сил инерции и в таком виде прикладывают
кзвену механизма.
Вплоских механизмах звенья могут совершать три вида движения: возвратно-поступательное, вращательное и сложное. Силы инерции определяются в зависимости от характера движения, совершаемого звеном.
2.2.3. Силы инерции звена, совершающего возвратно-поступательное движение
Этот вид движения характерен тем, что траектории, скорости и ускорения всех точек звена одинаковы. Рассматривая звено как неизменяемую систему одинаковых элементарных масс, каждая из которых развивает элементарную силу инерции, будем иметь систему параллельных одинаковых, направленных в одну сторону сил. Равнодействующая таких сил по аналогии с системой элементарных сил веса будет приложена в центре тяжести звена. Эта сила будет лишь больше или
37

меньше силы тяжести – это зависит от ускорения, с которым оно движется (рис. 2.12).
_ _
Pu= – mas 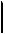
S |
as |
_ _ |
|
P=mas |
|
|
Рис. 2.12 |
|
На этом примере легко проследить осуществление принципа Даламбера. Действительно, если звено движется поступательно с ускорением as, это значит, что на него действует неуравно-
вешенная сила P mas . Для того чтобы тело находилось в равновесии, достаточно к его центрутяжести приложить равную и противоположную силу Pu mas . Тогда в этот момент сумма всех силстанет равной нулю, т.е. наступает состояниеравновесия.
Итак, равнодействующая сила инерции звена, движущегося поступательно, равна произведению его массы на ускорение и приложена в центре масс звена. Система сил инерции в данном случае приводится к равнодействующей.
2.2.4. Силы инерции звена, совершающего вращательное движение вокруг неподвижной оси
Применяя теорему об изменении количества движения и считая, что звено совершает поступательное движение вместе с системой координат, начало которой находится в центре тяжести звена (рис. 2.13), получим
Pn dQ |
d miVi d mVS |
maS , |
||||||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
dt |
|
dt |
1 |
|
|
dt |
|
|
|
|
|
|
где aS aS aSn , модуль aS найдем по теореме Пифагора.
aS 
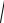 aS 2 a3n 2 rS
aS 2 a3n 2 rS 
 2 4 ,
2 4 ,
тогда модуль силы инерции
Pu mrS 
 2 4 .
2 4 .
38

|
|
Pu’ |
|
|
|
|
|
|
|
|
|
_ |
O |
|
_ |
|
y |
as |
|
Pu |
|
||
|
|
_n |
_ |
|
|
as |
|
|
|
as |
|
_ |
_ |
|
x |
Pu= – mas |
|
|
|
|
|
_ |
_ |
|
|
Mus= – Js |
|
Рис. 2.13
Главный момент сил инерции относительно центра тяжести найдем по теореме об изменении кинетического момента инерции той же точки:
M |
|
|
dKS |
|
d |
J |
|
|
J |
|
d |
|
J |
|
|
. |
|
dt |
|
|
|
|
|
||||||||||
|
uS |
|
|
dt |
S |
|
|
S dt |
S |
|
|
|||||
Таким образом, во вращательном движении система сил инерции при выборе центра приведения в центре тяжести приводится к главному вектору и главному моменту сил инерции. Систему сил инерции можно представить и другой эквивалентной системой сил, выбирая за центр приведения, например, ось вращения звена, и перенося в него главный вектор сил инерции, будем иметь главный вектор, геометрически равный его прежнему значению, а складывая моменты (прежний момент и момент, получающийся в результате переноса силы из точки S в точку 0), получим главный момент сил инерции относительно нового центра приведения 0:
Muo JS PnrS JS maS S JS mr32 J0 .
39

Можно найти и такой центр приведения, для которого Mи=0, т.е. такую точку, в которой приложена равнодействующая сил инерции. Такой точкой будет центр качания звена.
2.2.5. Силы инерции звена, совершающего плоское движение
Здесь также можно найти такой центр приведения, для которого Mu=0, т.е. система сил инерции может быть сведена к равнодействующей. Как видим, только в случае поступательного движения линия действия равнодействующей сил инерции проходит через центр тяжести звена (рис. 2.14).
dQ
Pu dt maS .
MuS dKS d JSa JS . dt dt
y
А  Mu _
Mu _
Pu
S x
as
B
O
b aBA  s
s 

a
Рис. 2.14
40
