
Учебное пособие 1878
.pdf1.4. Структурная формула кинематической цепи общего вида
Если на звено не наложено никаких условий связи, то оно в пространстве имеет шесть степеней свободы. N звеньев, не соединенных кинематическими парами, имеет 6N степеней свободы или 6n независимых движений.
Соединим N звеньев парами I, II, III, IV, V классов. Пусть количество пар:
I класса = Р1,
II класса = Р2,
III класса = Р3,
IV класса = Р4,
V класса = Р5.
Известно, что в зависимости от класса кинематической пары на относительное движение звеньев налагается определенное число условий связи, т.е. ограничений движения. Общее число условий связи, налагаемое всеми парами будет:
5P5 + 4Р4 + 3Р3 + 2P2 +P1.
Число же степеней свободы кинематической цепи
Н = 6N – (5P5 + 4Р4 + 3Р3 + 2P2 + P1).
Если одно звено этой цепи обратим в стойку, тогда число степеней свободы всей цепи уменьшится на шесть, т.е. Н – 6 = W – число степеней свободы кинематической цепи относительно стойки.
W = 6N – 6 – (5P5 + 4Р4 + 3Р3 + 2P2 +P1);
W = 6(N – 1) – (5P5 + 4Р4 + 3Р3 + 2P2 +P1);
W = 6n – (5P5 + 4Р4 + 3Р3 + 2P2 +P1),
где W – число степеней свободы кинематической цепи относительно стойки, N – число звеньев, n – число подвижных звеньев. Это выражение было дано в 1897 году Сомовым и несколько изменено Малышевым в 1923 году, получило название формула Сомова-Малышева для пространственной цепи.
11

Пусть имеется пространственная кинематическая цепь из трёх звеньев, имеющая две кинематические пары 5-го класса и по одной 3-го и 4-го классов. Тогда степень свободы такой цепи W определяется следующим образом (рис. 1.10).
Таким образом, рассматриваемая кинематическая цепь имеет степень свободы относительно стойки равную единице (одно независимое движение).
Механизм представляет собой кинематическую цепь, звенья которой совершают вполне определенные движения. Как же связана определенность движения звеньев механизма со степенью свободы?
В |
2 |
С |
3
1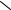
D
А
n=3; P5=2; P4=1; P3=1; W=6n – 5P5 + 4Р4 + 3Р3 + 2P2 +P1;
W=6 3–5 2–4 1–3 1=1.
Рис. 1.10
Если степень свободы W=1, это значит, что одному звену механизма можем предписать определенный закон движения, т.е. задать одну обобщенную координату, все остальные звенья будут совершать определенные движения.
Обобщенные координаты механизма – это независимые между собой координаты, определяющие положение всех звеньев механизма относительно стойки.
Звено, которому предписан определенный закон движения (задана обобщенная координата), называется начальным звеном. Часто начальное звено является входным. Число степеней свободы определяет количество начальных звеньев или обобщенных координат.
12
1.5. Структурная формула плоских механизмов
Для пространственного механизма степени свободы возможно определить по формуле Сомова-Малышева. Если же на движение звеньев механизма наложены общие условия связи, т.е. дополнительные требования, то это сказывается на характере движения звеньев и, следовательно, изменится структурная формула подвижности механизма.
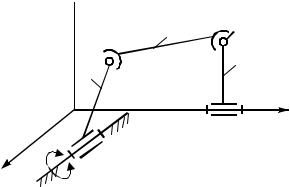
Рассмотрим механизм пространственного четырехзвенника (рис. 1.11).
z 
|
|
C |
|
|
2 |
|
1 |
3 |
|
|
|
x |
|
y |
|
D |
А
n=3; P5=2; P4=1; P3=1; W=6n – 5P5 + 4Р4 + 3Р3 + 2P2 +P1;
W=6 3–5 2–4 1–3 1=1.
Рис. 1.11
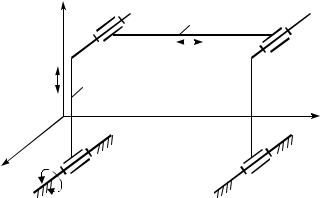
Задана одна обобщенная координата, имеем одно начальное или ведущее звено. Теперь поставим дополнительные требования – оси всех вращательных пар должны быть параллельны оси X (рис. 1.12). Это приведет к тому, что механизм обратится в плоский. Здесь невозможны три движения – вращение вокруг осей Y и Z и перемещение по X. Возможно вращение вокруг X и перемещение по Z и Y. Это обстоятельство влечет за собой изменение и структурной формулы:
W = (6 – 3) n – (5 – 3) P5 – (4 – 3) Р4 = 3n – 2P5 – Р4.
13
Это выражение, определяющее степень свободы плоского механизма, выведено Чебышевым в 1869 году.
Применим его к рассматриваемому механизму:
n=3, P5= 4, Р4=0,
W=3 3–2 4=1,
т.е. необходимо также одно начальное звено. Выберем в его качестве звено АВ.
z |
B |
2 |
C |
|
|
|
|
|
1 |
|
|
y
x
А D
Рис. 1.12
В соответствии с формулой Чебышева плоские механизмы могут содержать только пары 5-го и 4-го классов.
1.6. Пассивные связи и лишние степени свободы
Основное, что определяет движение механизма – это число степеней свободы и число условий связи. Но существуют степени свободы и условия связи, которые не влияют на характер движения звеньев. Такие степени свободы являются лишними, а условия связи – избыточными.
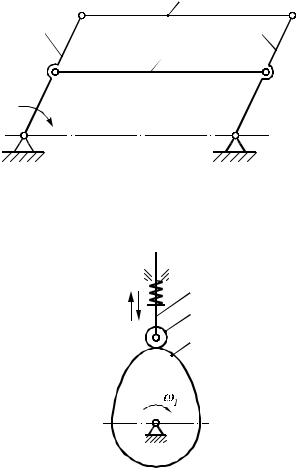
Рассмотрим механизм (рис. 1.13). Степень подвижности этой кинематической цепи W = 0. В действительности же это механизм. Звено BE создает избыточные связи, оно ставится в механизме исходя из конструктивных соображений; если же его удалить, характер движения остальныхзвеньев не изменится.
14
C |
2 |
|
D |
||
1 |
3 |
|
B |
4 |
|
E |
||
|
||
А |
F |
n=4; P5=6; W=3 4-2 6=0.
Рис. 1.13
Рассмотрим кулачковый механизм (рис. 1.14).
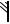
 0
0
2
3
1
n=3; P5=3; P4=1; W=3 3–2 3-1=2.
Рис. 1.14
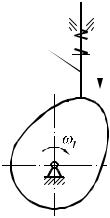
W = 2. Нужны два ведущих звена? Нет. Одну лишнюю подвижность дает ролик (звено 3), он вращается вокруг своей оси и поднимается вместе с толкателем. Если профиль кулачка выполнить по эквидистантной кривой, то механизм примет вид, представленный на рис. 1.15.
Следовательно, ролик, поставленный для уменьшения трения, дает лишнюю подвижность.
15
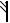
 0 2
0 2  1
1


n=2; P5=2; P4=1; W=3 2–2 2-1=1.
Рис. 1.15
Пассивные связи и лишние степени свободы могут быть выявлены при изучении кинематики механизмов. Так, если определение перемещений и скоростей можно произвести без участия отдельных звеньев, значит, они вносят либо избыточные связи, либо лишние степени свободы.
1.7. Замена в плоских механизмах высших кинематических пар низшими
В соответствии со структурной формулой Чебышева в плоские механизмы входят пары 5-го и 4-го классов. Часто пары IV класса могут быть высшими. Отдельные методы теории механизмов и машин требует замены высших пар звеньями, входящими только в низшие кинематические пары. При замене должны удовлетворяться следующие условия:
1)степень свободы должна остаться прежней;
2)характер движения звеньев не должен изменяться.
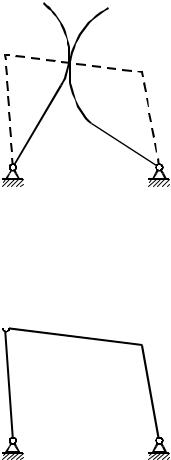
Рассмотрим механизм из двух подвижных звеньев n=2
(рис. 1.16).
Здесь две пары 5-го класса А и В и одна пара 4-го класса – высшая (точка контакта звеньев 1 и 2). Степень свободы данного механизма
16
|
W=3 2–2 2–1=1. |
O1 |
3 |
|
O2 |
|
1 |
A |
2 |
B |
Рис. 1.16
Покажем, что этот механизм может быть заменен шарнирным четырехзвенником (рис. 1.17).
Всякая высшая пара заменяется одним фиктивным звеном и двумя низшими кинематическими парами.
O1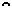
 O2
O2
A B
W = 3 3-2 4=1.
Оба предъявляемые к нему требования выполняются. О1О2– фиктивное звено; AO1 О2 B – заменяющий механизм.
Рис. 1.17
Величина фиктивного звена равна расстоянию между центрами кривизны элементов высшей пары.
О1О2 – фиктивное звено.
О1О2 = 1 2. Механизм AО1О2B является заменяющим.
17
1.8. Классификация плоских механизмов
Механизмы можно классифицировать по различным признакам.
1.Механизмы, в состав которых входят только низшие пары и, наоборот, высшие.
2.По конструктивным признакам: шарнирно-рычажные, зубчатые, кулачковые и др.
3.По характеру воспроизводимого движения: передающие вращательное, поступательное движения.
Можно привести ещё ряд классификаций. Однако наиболее общей из всех является классификация по АссуруАртоболевскому.
Прежде чем перейти к классификации, познакомимся с принципом образования механизмов. Впервые он сформулирован в 1914 году ученым Петербургского политехнического института Д.В. Ассуром и состоит в следующем: механизм создается путем последовательного наложения кинематических цепей, обладающих определенными структурными свойствами.
В этом определении дается основной принцип струк-
турного синтеза механизмов.
Структурным синтезом механизмов называется про-
ектирование структурной схемы механизма, под которой понимается схема механизма с указанной стойкой, подвижными звеньями, видами кинематических пар и их взаимным расположением.
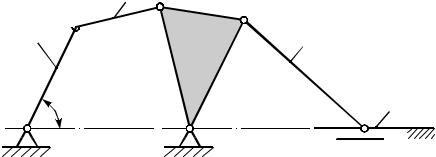
Принцип создания механизма проследим на примере плоского механизма. Рассмотрим следующий механизм
(рис. 1.18).
В этом механизме одно начальное или ведущее звено –
АВ (звено 1); задана одна обобщенная координата , которая определяет положение всех остальных звеньев относительно стойки. Звенья 2, 3, 4 и 5 – ведомые, стойка – 0. Как же образовался механизм?
18
B
1
А
0
2 C
E
3 4
F 5 D 
0
0
n=5; P5=7; W=1.
Рис. 1.18
Вначале к ведущему звену 1 и стойке 0 присоединили группу звеньев 2 и 3, получили механизм шарнирного четырехзвенника АВСD: n=3, P5=4, W=1. Затем к звену 3 и стойке присоединили звенья 4 и 5, получили данный механизм ABCDE, W=1. После присоединения к начальному звену звеньев 2, 3, 4, 5 степень свободы механизма не изменилась, это значит, что кинематическая цепь из звеньев 2, 3, 4, 5 имеет степень свободы равную нулю.
Кинематическая цепь, обладающая нулевой степенью свободы после присоединения ее свободными элементами к стойке, называется структурной группой или группой Ассура. Такая группа не должна распадаться на более простые группы, обладающие нулевой степенью свободы.
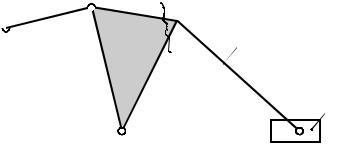
Кинематическую цепь из звеньев 2, 3, 4 и 5 можно разделить на две структурные группы: первая из звеньев 2 и 3, вторая из звеньев 4 и 5(рис. 1.19). Обе эти группы имеют W=0.
Кинематическая цепь из двух звеньев и трех кинематических пар является простейшей структурной группой. Такую группу называют группой II класса и 2 порядка.
19
2 C
 E B
E B

3 4
F 5
D
n=2; P5=3; W=3 2–2 3=0.
Рис. 1.19
Структурная группа должна удовлетворять следующему условию:
W=3n–2P5=0; 3n=2P5; P5=(3/2) n.
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
|
Подвижных |
n |
2 |
4 |
6 |
|
8 |
звеньев |
|
|||||
|
|
|
|
|
|
|
Кинематических |
P5 |
3 |
6 |
9 |
|
12 |
пар 5-го класса |
|
|||||
|
|
|
|
|
|
|
В таблице дается сочетание звеньев и кинематических пар, из которых могут быть составлены структурные группы.
Первое сочетание n=2, P5=3 представлено группой второго класса, которая имеет пять разновидностей.
Если группу второго класса присоединить к начальному звену и к стойке, получим механизм второго класса. Таких групп может быть сколько угодно, но это не меняет класс механизма.
Рассмотрим следующее сочетание: n=4, P5=6. Здесь возможны виды структурныхгрупп, представленныенарис. 1.20.
20
