
Учебное пособие 1696
.pdf
|
|
|
|
2 |
|
(n −1) |
= |
|
(−1)n −1(n −1)!2n |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||
|
1 + 2x |
|
|
|
(1 + 2x)n |
|
|
|
|
|
|||||||||||
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
||||||||||
y |
(40) |
|
|
(−1)39 39!239 |
|
|
|
|
2 |
|
39 |
|
|
|
|
||||||
|
= |
|
|
|
|
= −39! |
|
|
|
. |
|
|
|
|
|||||||
|
(1 + 2x)39 |
|
1 + 2x |
|
|
|
|
||||||||||||||
|
При |
п ≥ 2 будем иметь |
|
|
|
|
|
|
|||||||||||||
y(n) (x2 − x + 6) + ny(n −1) (2x −1) + |
n(n −1) |
y(n −2) |
2 = 0 , |
||||||||||||||||||
|
|||||||||||||||||||||
|
откуда при х = 0 получим |
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
6 y(n) (0) − ny(n −1) (0) + n(n −1) y(n −2) (0) = 0 |
|
|
|||||||||||||||||||
|
или y(n) (0) = |
n |
y |
(n −1) (0) − |
n(n −1) |
y(n −2) |
(0). |
||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
|
|||
Полученная рекуррентная формула, позволяет определить n-ю производную в точке х = 0 (п ≥ 2). Значения у(0) и y'(0) находятся непосредственно
|
1 |
|
′ |
|
− 2x2 − 6x +15 |
|
15 |
|
y(0) = |
|
, |
y (0) = |
(x2 − x + 6)2 |
= |
|
. |
|
2 |
36 |
|||||||
|
|
|
|
|
|
x =0 |
|
|
|
|
|
|
|
|
|
|
|
Полагая |
последовательно |
п = 2,3,4,..., с помощью |
||||||
рекуррентной формулы находим значения искомых производных. Так
|
′′ |
|
= |
2 |
y |
′ |
|
− |
2 |
1 |
y(0) |
= |
1 |
|
15 |
− |
|
1 |
= − |
1 |
, |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y (0) |
6 |
(0) |
|
6 |
|
3 |
36 |
|
|
36 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
′′′ |
|
3 |
|
′′ |
|
|
3 2 |
|
′ |
|
|
1 |
|
|
|
|
1 |
|
|
2 15 |
|
|
|
31 |
|
|||||||
= |
|
|
|
− |
|
|
|
|
|
= |
|
|
− |
|
|
|
− |
|
|
|
|
|
= − |
|
. |
|||||||
y (0) |
6 |
y (0) |
|
6 |
|
y (0) |
2 |
36 |
|
36 |
|
72 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2.4. Дифференциал функции
10. Из определения производной lim |
y |
= y′ |
и предела |
x→0 |
x |
|
|
71
|
y |
′ |
|
y = y |
′ |
x +α x , где |
|
переменной следует, что |
x = y |
+α или |
|||||
|
|
α→0 при x → 0 , т. е. приращение функции можно разбить на
две части. |
y′ x есть бесконечно малая первого |
|
Произведение |
порядка |
|
относительно |
х. Произведение же α x есть |
величина |
бесконечно малая высшего порядка относительно |
х, т.к. |
|
lim α = 0 . |
|
|
x→0 |
|
|
Первое слагаемое приращения функции называется
главной частью приращения. Произведение y′ x называется
дифференциалом функции и обозначается dy. Дифференциал независимой переменной х равен ее приращению, т.е. dx≈Δx.
Итак, если функция у = f(x) имеет производную f ′(x) в
точке x, то дифференциал функции равен произведению производной f ′(x) на дифференциал независимой
переменной, т. е.
|
′ |
|
|
|
|
(1) |
dy = f (x) dx. |
|
|
|
|
||
20. Правила дифференцирования: |
|
|
||||
1. d{Cu) = Cdu; |
2. d(u±v) = du±dv; |
|
||||
|
u |
|
vdu −udv |
|
||
3. d(uv) = udv + vdu; |
4. d |
|
|
= |
|
. |
|
v2 |
|||||
|
v |
|
|
|||
30. Геометрический смысл дифференциала. Дифференциал функции геометрически определяется разностью ординат касательной к кривой при переходе от точки с абсциссой х0 к точке с абсциссой x0 + x (рис. 2.7).
72

Рис. 2.7
40. Инвариантность формы дифференциала. Форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Если y = f (x) , где x = ϕ(t), то
dy = fx′dx = fx′ϕt′dt . |
(2) |
50. Дифференциалом второго порядка функции у = f{x) в некоторой точке называется дифференциал в этой точке от ее первого дифференциала и обозначается
|
|
d |
2 |
|
|
|
|
|
|
|
′′ |
|
2 |
. |
|
|
(3) |
|
|
|
y = d (dy) = y dx |
|
|
||||||||||||
Аналогично |
определяются |
дифференциалы высших |
|||||||||||||||
порядков |
3 |
|
|
|
2 |
|
|
′′′ |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
||||
d |
y=d(d |
y)= y dx |
|
|
|
|
|
|
|
||||||||
dny=d(dn-1y)=y(n)dxn |
|
|
|
|
|
(4) |
|||||||||||
60. Если функция |
сложная |
y |
|
= |
f(x), где х = ϕ (t), |
то |
|||||||||||
дифференциал |
второго порядка |
d2y=d( fx′dx) находится |
по |
||||||||||||||
формуле |
d2y = fxx′′dx2 + |
fx′dx, |
|
|
|
|
|
||||||||||
|
|
|
|
|
(5) |
||||||||||||
где dx = xt′dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциал третьего порядка будет |
|
||||||||||||||||
3 |
′′′ |
|
|
3 |
+ |
3 f |
′′ |
dx d |
2 |
x + f |
′ |
d |
3 |
(x). |
(6) |
||
d y= f |
(dx) |
|
|
|
|
|
|||||||||||
и т. д. Здесь штрихами обозначено дифференцирование по х.
73

70. Для дифференцируемой функции |
y = f(x) из |
|
приближенного равенства |
y ≈ dy следует |
|
f(x+ x) ≈ f(x)+ f |
′ |
(7) |
(x) x . |
||
Эту формулу используют при приближенных вычислениях. 80. Абсолютная величина разности между истинным
значением какой-либо величины a0 и ее приближенным значением а называется абсолютной погрешностью и
обозначается |
= |
|
a0 − a |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Абсолютная |
|
|
|
величина |
отношения |
абсолютной |
||||||||||||||||||||||||||||
погрешности |
|
|
к |
|
|
|
истинному |
значению |
|
|
|
называется |
||||||||||||||||||||||
относительной погрешностью и обозначается δ = |
|
|
|
|
|
. |
|
|
||||||||||||||||||||||||||
|
a |
|
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Относительная погрешность обычно выражается в |
||||||||||||||||||||||||||||||||||
процентах |
|
δ = |
|
|
|
|
100 %. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если приращение функции заменить ее дифференциалом, |
||||||||||||||||||||||||||||||||||
то получим приближенное значение приращения |
|
|
y ≈ dy . В |
|||||||||||||||||||||||||||||||
этом случае абсолютная погрешность равна |
= |
|
|
y − dy |
|
, а |
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
относительная погрешность будет δ = |
|
|
y − dy |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.1. Найти дифференциалы функций: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
ln tgx |
; в) y = |
x3 −1 |
|
|
|
|
|
|
|
|
|
||||||
а) y = x |
|
− x + |
|
|
|
x ; б) y = 3 |
|
|
; |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x3 +1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
г) |
x = a sin3 t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. а) Находим производную данной функции |
||||||||||||||||||||||||||||||||||
y |
′ |
= 3x |
2 |
−1 + 2 |
1 |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Отсюда дифференциал равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
2 |
−1 + |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dy = y dx = 3x |
|
|
dx. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
|||||||
74

б) Находим производную
y |
′ |
lntgx |
1 1 |
|
2 3lntgx ln 3 |
|
|||
|
= 3 |
ln 3 |
|
|
|
= |
|
. |
|
|
tgx |
cos2 x |
sin 2x |
||||||
Отсюда дифференциал
dy = 2 3ln tgx ln 3 dx. sin 2x
в) Находим производную
y |
′ |
|
3x2 (x3 |
+1) −(x3 |
−1) 3x2 |
|
6x2 |
|
||
= |
|
|
(x3 +1)2 |
|
|
= (x3 +1)2 . |
||||
|
|
|
|
|
||||||
Отсюда дифференциал будет |
|
|
|
|||||||
|
|
|
dy = |
6x2 |
|
dx . |
|
|
|
|
|
|
|
(x3 +1)2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
г) Производная по t равна x′ = 3asin2 t cost . Отсюда дифференциал dx = 3a sin2 t cos t dt.
4.2. Найти дифференциалы указанных порядков от функции:
а) |
|
y = 3ln tgx , d 2 y ? ; |
|
б) |
ρ = |
sin 2ϕ |
, d 2 |
ρ? |
||||||||||||
|
|
1 −ϕ2 |
|
|||||||||||||||||
в) y = (x2 − x +1)3 , d 3 y ? |
|
г) x 13 + y 13 = a 13 , d 2 y ? |
||||||||||||||||||
Решение. а) Находим дифференциал 1-го порядка |
|
|||||||||||||||||||
|
|
lntgx |
1 |
1 |
|
|
|
3lntgx |
|
|
|
|
|
|||||||
dy = 3 |
ln 3 |
|
|
|
|
dx = 2 ln 3 |
|
dx. |
|
|
|
|
|
|||||||
tgx |
cos2 x |
sin 2x |
|
|
|
|
|
|||||||||||||
Дифференцируя еще раз, получим |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
3lntgx sin 2x |
lntgx |
cos 2x |
|
|
|
|
|
||||||
|
|
|
|
2 ln 3 |
|
|
|
−2 3 |
|
|
|
|
|
|||||||
d |
2 |
y = 2 ln 3 |
|
|
sin 2x |
|
dx |
2 |
= |
|
||||||||||
|
|
|
|
|
sin2 |
2x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 4 ln 3 3lntgx ln 3 −cos 2x dx2 . sin2 2x
б) Дифференцируя последовательно дважды, имеем
75
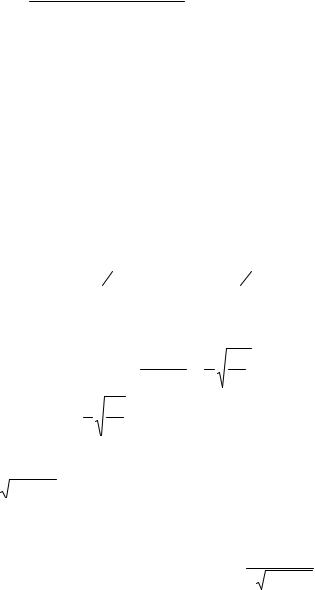
dρ = 2 cos 2ϕ(1 −ϕ2 ) +ϕsin 2ϕ dϕ. (1 −ϕ2 )2
d 2 ρ = 2((−sin 2ϕ 2(1 −ϕ2 ) −cos 2ϕ 2ϕ +sin 2ϕ +
+ 2ϕcos 2ϕ)(1 −ϕ2 )2 + 2(cos 2ϕ(1 −ϕ2 ) +ϕsin 2ϕ)(1 −ϕ2 )4 = = 2(sin 2ϕ(5ϕ2 −1 − 2ϕ4 ) + 2ϕcos 2ϕ(1 −ϕ2 ))dϕ2.
в) Дифференцируя последовательно три раза, имеем dy = 3(x2 − x +1)2 (2x −1)dx,
d 2 y = 3(2(x2 − x +1)(2x −1)2 + (x2 − x +1)2 2)dx2 = = 6(x2 − x +1)(5x2 −5x + 2)dx2 ,
d 3 y = 6((2x −1)(5x2 −5x + 2) + (x2 − x +1)(10x −5))dx3 =
= 6(2x −1)(10x2 −10x + 7)dx3.
г) Функция задана неявно. Находим первую производную
|
y |
23 |
|
|
|
|
|
|
y |
23 |
||||||||
|
y′ = − |
|
|
|
|
|
, тогда dy = − |
|
|
|
dx. |
|||||||
|
|
|
|
|
|
|
||||||||||||
|
x |
|
|
|
|
|
|
|
|
x |
|
|
||||||
Вычисляем вторую производную |
|
|
|
|
||||||||||||||
|
|
|
|
2 y |
− |
1 |
|
′ |
|
2 |
ay |
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
y′′ = − |
|
|
|
|
|
|
|
3 |
|
= |
|
|
|
|
, |
||
|
3 |
|
|
|
|
x2 |
3 |
x5 |
||||||||||
|
|
|
x |
|
|
|
|
|
||||||||||
отсюда |
d 2 y = |
2 3 |
ay dx2. |
|
|
|
|
|
|
|
||||||||
|
|
|
3 |
|
|
x5 |
|
|
|
|
|
|
|
|
|
|
||
4.3. Выразить дифференциал сложной функции через независимую переменную и ее дифференциал:
а) |
y = x2 −3x, x = t2 +1; б) z = ln y, y = tgx, x = 2t2 +t; |
||
в) |
y = ex , |
x = tgt , представить d 2 y |
через: 1) x и dx; 2) t и dt. |
|
Решение. a) Дифференциал сложной функции равен |
||
|
|
|
2x −3 |
dy = y′x xt′dt. |
Находим производные |
y′x′ = 2 x2 −3x ; |
|
xt′ = 2t.
76

Подставляя значение x в y′x , окончательно получим
|
dy = |
(2t2 |
−1)tdt |
. |
|
|
|
||
|
(t2 +1)(t2 − 2) |
|
|
|
|||||
|
|
|
|
|
|
||||
б) Дифференциал сложной функции в этом случае имеет |
|||||||||
вид dz = z′y |
y′x xt′dt. |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
||
Находя |
производные |
z′y = |
|
, |
y′x = |
|
, |
xt′ = 4t +1 и |
|
y |
cos2 x |
||||||||
подставляя их значения в выражение дифференциала,
окончательно получим dz = |
1 |
|
1 |
(4t +1)dt = |
2(4t +1)dt |
. |
||
|
cos2 x |
sin(2(2t2 +t)) |
||||||
|
|
y |
|
|
||||
в) Находим |
дифференциал |
первого |
порядка |
|||||
dy = y′x dx = ex dx. |
Дифференциал второго порядка через x и dx |
|||||||
равен d 2 y = y′′xx dx2 = exdx2 .
Выразим теперь дифференциал через t и dt. Дифференциал
первого порядка будет dy = |
y′x xt′dt = ex |
|
1 |
|
|
dt = etgt |
|
dt |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||
cos2 |
|
x |
|
cos2 t |
|
|
|
||||||||||||||||||||||||||||||||||
Дифференцируя по t, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
e |
tgt |
|
1 |
|
cos |
2 |
t +e |
tgt |
2sin t cos t |
|
|
|
tgt 1 |
+sin 2t |
|
|
|
|
||||||||||||||||||
|
|
2 |
|
|
|
cos2 t |
|
|
|
|
|
2 |
|
|
2 |
|
|
||||||||||||||||||||||||
d |
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
= e |
|
|
|
cos4 t |
dt |
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
cos4 t |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Если воспользоваться формулой (5), |
где |
fx′ = ex , |
fxx′′ |
= ex , |
|||||||||||||||||||||||||||||||||||||
dx = |
|
|
dt |
|
|
|
, то придем к такому же результату |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
x dt2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
x |
|
|
dt |
|
|
tgt 1 |
+ sin 2t |
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
d |
|
|
|
y = e |
|
|
|
|
+ e |
d |
|
|
|
= e |
|
|
|
|
|
|
|
|
dt |
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
cos4 t |
|
|
|
|
|
|
cos4 t |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4.4. Вычислить приближенно: a) |
|
arctg 1,05; |
6) |
|
lg 9; |
||||||||||||||||||||||||||||||||||||
в) 5 0,98 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. a) Полагаем f ( x ) = arctgx, тогда f |
′ |
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
(x) = 1 + x2 . |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Отсюда no формуле (7) имеем |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
arctg(x + |
x) = arctgx + |
|
|
|
x. |
|
|
|
|
|
|
|
|
|||||||||||||
1 + x2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть x = 1, тогда х = 0,05. Таким образом |
|
|
|
|
|
|
||||||||||||||||||||
arctg(1 + 0,05) = arctg1 + |
1 |
0,05 = π |
+ 0,025. |
|
||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
1 +1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||
б) Положим f ( x ) = lgx, тогда |
′ |
|
1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
f |
(x) = x ln10 . Отсюда по |
|||||||||||||||||||||||||
формуле (7) имеем |
lg(x + |
|
x) = lg x |
+ |
|
|
|
x |
. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x ln10 |
|
|
|
|
|
|
−1 |
|
|||||||
Пусть x =10, тогда |
x = -1 и lg(10 −1) = lg+ |
|
|
|
|
. |
||||||||||||||||||||
10ln10 |
||||||||||||||||||||||||||
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отсюда lg9 =1 − |
|
= 0,956. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ln10 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
′ |
|
1 |
|
− |
|
|
|
|
1 |
1 |
|||||||
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|||||||||||
в) Полагаем f (x) = |
|
x , |
тогда |
f |
(x) |
= |
|
x |
|
|
|
|
= |
5 5 |
x4 . |
|||||||||||
|
5 |
|
|
|
|
|||||||||||||||||||||
Отсюда 5 x + |
x = 5 |
x |
+ |
1 |
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
5 |
55 x4 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
−0,02 или |
|||||
Пусть x = 1, тогда |
х = 0,02 и |
5 1 −0,02 = 5 1 + |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 14 |
|
|||
5 0,98 =1 −0,0004 = 0,996 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4.5. Для функции |
|
|
y = x2 +3x +1 |
найти |
приращение |
|||||||||||||||||||||
ординаты касательной и приращение функции при переходе аргумента x от значения х=2 к х=2,1.
Решение. Согласно геометрическому смыслу дифференциала, приращению ординаты касательной соответствует дифференциал функции dy = (2x +3)dx .
При х = 2 и dx = x = 2,l – 2 = 0,l получим dy = (2 2+3) 0,1 = 0,7.
Приращение функции находим по формуле
78
y = f (x + x) − f (x) = (2,12 +3 2,1 +1) −(22 +3 2 +1) = =11,71 −11 = 0,71.
Следовательно, приращение ординаты касательной равно
0,7, |
а приращение функции 0,71. Так как |
у = dy + α х, то |
||
α х = 0,71 - 0,7 = 0,01. |
|
|
||
4.6. |
Найти |
дифференциал и |
приращение функции |
|
y = x3 − 2x при |
х = 2 и х = 0,1. |
Найти |
абсолютную и |
|
относительную погрешности при замене приращения функции её дифференциалом.
Решение. Имеем: dy = (3x2 − 2)dx ,
y = ((x + x)3 − 2(x + x)) −(x3 − 2x) = (3x2 +3x x + x2 − 2) x
При x = 2 и x = |
0,l |
получим: dy = (3 22 − 2) 0,1 =1; |
|||||||
y = (3 22 +3 2 |
0,1 |
+ 0,12 − 2) 0,1 =1,061. |
|||||||
Абсолютная погрешность |
= | у - dy| = 0,061, а oтноси- |
||||||||
тельная погрешность δ = |
|
|
|
|
100% = |
0,061 |
100% ≈ 6% . |
||
|
y |
|
|
|
|||||
|
|
|
|
|
1,061 |
|
|||
4.7. При измерении сторона куба х оказалась равной 4см, причём максимально возможная при этом погрешность измерения х находится в пределах ± 0,01см. Определить абсолютную и относительную погрешности при вычислении объёма куба.
Решение. Объём куба равен V = x3 = 64 см3. Возможная
неточность |
измерения |
| |
х | = 0,01. Отсюда абсолютная |
||||||||||
погрешность |
|
V |
|
≈ |
|
|
|
dV |
|
|
= 3x2dx = 3 42 0,01 = 0,48. Относи- |
||
|
|
|
|
||||||||||
тельная погрешность |
|
dV |
|
|
0,48 |
100% = 0,75% . |
|||||||
|
|
|
= |
||||||||||
V |
|
64 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
79

2.5. Приложения производной к задачам геометрии и физики
10. Уравнение касательной и нормали к кривой. Значение производной f ′(x) в некоторой точке x = x0 геометрически
представляет угловой коэффициент касательной к графику функции y = f (x) в точке x = x0 .
Из геометрического смысла производной следует, что угловой коэффициент касательной к кривой y = f (x) (рис. 2.8) в точке M (x0 , y0 ) M y равен значению производной в этой
точке, т. е. k = tgα = f ′(x0 ) . Поэтому, если в уравнение пучка
прямых, проходящих через точку М, подставить угловой коэффициент касательной, то уравнение касательной к кривой в данной точке примет вид y − y0 = f ′(x)(x − x0 ).
Нормалью к кривой в точке M (x0 , y0 ) называется пря-
мая, проходящая через точку M перпендикулярно касательной и кривой в этой точке. В силу условия перпендикулярности
двух |
прямых |
|
k1 |
= − |
1 |
, уравнение нормали имеет вид |
|||
|
|
||||||||
|
|
|
|
|
|
k2 |
|
||
y − y0 |
= − |
1 |
|
(x − x0 ) , если |
f ′(x0 ) ≠ 0 . |
||||
f ′(x0 ) |
|||||||||
|
|
|
|
|
|
|
|||
Отрезки |
AM = y0ctgα , |
BN = y0tgα называются, соответ- |
|||||||
ственно подкасательной и поднормалью, а длины отрезков АМ и ВМ – длинами касательной и нормали.
Рис. 2.8
80
