Учебное пособие 1696

в) Функция определена на всей числовой оси. Находим

x1=1. При переходе через точку x1 = 1 производная у' меняет знак с минуса на плюс, следовательно, в точке x1 = 1 функция имеет минимум y(1) = −1.

Приравнивая к нулю знаменатель производной, получаем 5 x =0. Отсюда находим критическую точку функции x2 = 0, в которой производная не существует. Очевидно, что в точке x − 0 производная y′ > 0 , а в точке x + 0 производная y′< 0.

Рис. 2.27

Производная y′ = 0 тогда, когда Fx′ = 0 , т. е. y 2 - 2ху = 0. Решая совместно систему

xy2 − x2 y = 2a3 ,

y 2 − 2xy = 0,

111

находим критическую точку х = а, у = 2а.

ляем ее знак в критических точках. Поскольку при x = 0, y = 0 и Fy′ = 0 , то в окрестности этой точки уравнение может

определять у как неоднозначную функцию от x, поэтому точку (0,0) оставляем в стороне.

112

точках и в точках на концах отрезка. Из сравнения видно, что наибольшее значение функции будет y(1) = 12 , а наименьшее

y(−1) = − 12 . График функции на отрезке [-2;2] показан на рис. 2.28.

В данном случае имеем только одну критическую точку

x = 12π .

Вычисляем значение функции в критической точке и на концах отрезка

114

Сравнение найденных значений функции показывает, что

ции на отрезке [0; π3 ] показан на рис. 2.29.

x2 + 2x −3 = 0, x1 =1, x2 = −3. Поскольку критические точки лежат внутри отрезка [−6,2] , вычисляем значения функции в критических точках y(1) =15, y(−3) = 47 . Находим значение функции на концах отрезка y(−6) = −34, y(2) = 22 .

Сравнивая вычисленные значения функции в критических точках и на границе отрезка, заключаем, что наибольшее значение находится в критической точке x = −3 и равно y(−3) = 47 , а наименьшее в граничной точке x = −6 и равно

у{-6) = -34 (рис. 2.30).

115

б) Функция определена на всей числовой оси. Изменение аргумента не ограничено отрезком, поэтому рассмотрим значения функции при x ]−∞;∞[.

Находим производную

2sin x cos x(sin 2 x − cos2 x) = 0 , откуда sin2xcos2x = 0, sin2x = 0,

ет. Значение функции при х = 0 равно -1. При x → ±∞ функ-

Рис.2.32

117

2.11. Решение задач на максимум и минимум

При решении задач на максимум и минимум по условиям задачи следует составить функцию, приняв одну из переменных за основную и выразив все остальные переменные через нее.

Далее следует исследовать эту функцию на экстремум по искомой переменной, т. е. найти наибольшее или наименьшее значение полученной функции. Интервал изменения независимой переменной определяется из условий задачи.

11.1. Объем цилиндра V. Найти радиус основания, при котором цилиндр имеет наименьшую полную поверхность.

Решение. Полную поверхность цилиндра принимаем за

равнивая ее к нулю 2R − πVR2 = 0, находим, что минимум наи-

меньшей полной поверхности будет при радиусе R = 3 2Vπ .

То есть найденное значение радиуса определяет наименьшую полную поверхность.

118

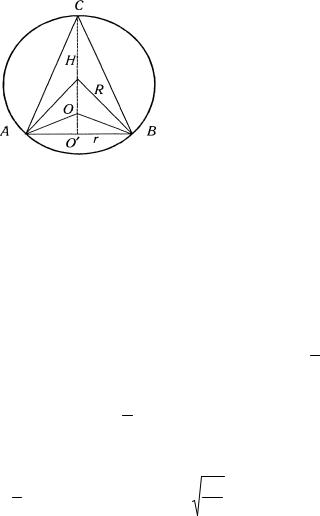
11.2. В данный шар вписать конус с наибольшим объе-

мом.

Решение. Объем конуса, вписанного в шар (рис. 2.33),

равен V = 13 πHr 2 , где Н - высота конуса, г - радиус основания.

Рис. 2.33

функцию, наибольшую его величину находим, исследуя эту функцию на экстремум:

VH′ = π3 (4HR −3H 2 ), 4HR −3H 2 = 0, H = 0, H = 43 R .

При Н = 0 функция, естественно, не может иметь наи-

большего объема. При Н = 43 R производная VH′ меняет знак с

плюса на минус, т. е. функция имеет максимум. Следовательно, наибольший объем конуса, вписанного в шар, при высоте

конуса H = 43 R где радиус шара R = 3 34Vπ .

119

B(−2 3;1) . Найти на данном эллипсе третью точку С такую,

чтобы площадь треугольника ABC была бы наибольшей. Решение. Обозначим координаты искомой точки С за x, у, тогда площадь треугольника по формуле

S = 12 [x1 ( y2 − y3 ) + x2 ( y3 − y1 ) + x3 ( y1 − y2 )] будет иметь вид S = 12 ( 3(1 − y) − 2 3( y + 2) + x(−2 −1)) =

При отрицательном значении y производная знака не меняет. При переходе через точку

120