Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1696

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.8 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 234 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

x = x2 - x1=2 – 1 = 1. Вычислим исходное значение функции

y(x1) = 2 13 - 3 1 + 1 = 0.

Вычислим новое значение функции

y(x1 + x) = y(1+1) = 2 23 - 3 2 + 1 = 11.

Отсюда приращение функции

		y=y( x1 +	x ) - y( x1 ) = 11.
5.2. Найти приращение функции y=3 x2 -2x+4 и вычислить
его при x = 2 и		x = - 0,1.
Решение.		Новому	значению	аргумента	x+ x
соответствует новое значение функции
		y(x + x) = 3(x + x)2 - 2(x + x) + 4.
Приращение функции равно y=y(x +				x)-y(x)=
=3(x +	x)2 - 2(x + x) + 4 - 3x2 - 2x – 4 = (3			x+6x-2)	x. При
х =2 и	x = - 0,1	получим y = (-0,3 + 12 - 2)(-0,1) = 0,97 .

5.3.Найти множество значений х, при которых функция

у= x3 - 2x непрерывна.

Решение. Найдем приращение функции
y=(x + x)3 - 2(x + x) - (x3-2x) = x( x2+3x	x+3x2-2).
При любых значениях х приращение	y→0, если

только x→0, поэтому функция непрерывна при всех действительных значениях х.

5.4. Доказать непрерывность функции y =

в точке

x −1

х = 3.

Решение. Для доказательства найдем приращение

функции

при

переходе

значения аргумента от

х = 3 к

х = 3 + х

2 − 2 − x

− x

−

x −1

−1

2(2 + x)

2(2 +

Найдем предел приращения функции при

x→0.

lim

y = − lim

= 0.

2(2

x→0

Так как предел приращения функции при

x→0 равен

нулю, то функция при x = 3 непрерывна.

5.5. Найти приближенно хотя бы один корень уравнения

3x3 + 2x2 – x – 1 = 0.

Решение. Найдем точку пресечения графика функции y=3x3 + 2x2 – x – 1 = 0 с осью Ох, то есть точку, в которой у = 0.

Подберем две произвольные точки, в которых функция имеет разные знаки. Пусть х =0, тогда у = - 1 , у < 0. При х = 1, у = 3 + 2 - 1 - 1 = 3, у > 0 . Значит, корень находится между x= 0 и х = 1 (в силу свойства непрерывности).

	Определим знак функции в середине промежутка [0,1], т. е.
при х =0,5.
	Находим y=3 0,53+2 0,52-0,5-1=-0,625; y < 0. Значит, корень
находится между х = 0,5 и х = 1.
	Определим знак функции в середине этого промежутка,
т.е. при x =		3					3		3		3	2	−	3		−1 =	41
т.е. при x =			. Находим y =				3		+ 2				−			−1 =		.
		4						4			4			4			64
	Следовательно,				корень		находится				внутри					промежутка
1 ,	3 . Находим знак функции в середине этого промежутка,

2	4
т.е. при x =		5	5	3	5	2		5		213			71
			, 3		+ 2		−		−1 =			=			>0.
		8	, 3		+ 2		−	8	−1 =	192		=	64		>0.
		8	8		8			8		192			64

Значит, корень находится внутри промежутка 12 , 85 .

Можно уже считать, что x = 169 . Если требуется большая

точность, то указанный процесс приближений может быть продолжен дальше.

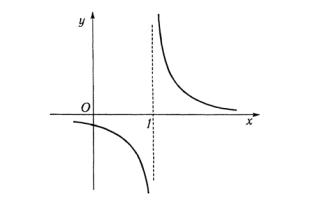
5.6. Определить характер разрыва функций: а) y=				1
				x −1
		2x, при	x ≠ 2,
при x = 1; б) y=	x
		при x = 0; в) y=
	x		x = 2.
		1, при

1			1
г) y= a	x	(a>1); д) y=arctg		и построить графики.
			x

Решение. а) При х = 1 функция				не определена:
lim	1	= −∞;	lim		1	= +∞.
	x −1
x→1−0			x→1+0 x −1

Следовательно, при х = 1 функция имеет разрыв второго рода (рис. 1.7).

Рис. 1.7

б) При x<0 предел равен lim

= −1 = k

, при х > 0 предел

x→1−0

равен

lim

=1 = k2 . Следовательно, при х = 0 функция

x→1+0

имеет

разрыв

первого рода

скачок

функции равен

k1 − k2

−1 −1

= 2 (рис. 1.8).

		Рис. 1.8
в) Функция	определена		на	всей		числовой оси,
неэлементарная,	так как	в	точке		x = 2	аналитическое
выражение функции меняется.
Исследуем непрерывность функции в точке х = 2:
lim 2x = 4 ,	lim 2x = 4 ,	y(2)=1,		k1	= k2 ≠ k3 .
x→2−0	x→2+0

Очевидно, что в точке х = 2 функция имеет устранимый разрыв (рис. 1.9).

г) Найдём пределы:		Рис. 1.9

1		1
y(+0) = lim a	x	= +∞, y(-0) = lim a	x	= 0.
x→+0		x→−0

Вточке x=0 справа функция имеет разрыв второго рода,

аслева — непрерывность (рис. 1.10).

д) Найдем пределы:					Рис. 1.10
			π					π .
y(+0)= lim arctg	1	=		,	y(-0)= lim arctg	1	= −
	x		2			x
x→+0					x→−0			2

В точке x=0 с обеих сторон скачки (рис. 1.11).

	Рис. 1.11
5.7. Дана функция	1
	y =		,	и три значения
		x2 + 4x −5
аргумента x1 = -5, x2 = 0,	x3 = 1. Выяснить,			является ли данная

функция непрерывной или разрывной для каждого из данных

значений х? Сделать чертеж.
Решение. Исследуем		непрерывность			функции в точке
x = -5:	1				1
lim		= ∞, lim				= −∞.
	x2 + 4x −5		x2	+ 4x −5
x→−5−0		x→−5+0
		35

Следовательно, при х1 = -5 функция имеет разрыв второго рода (рис. 1.12).

Рис. 1.12

При x2 = 0 пределы слева и справа равны:

lim

= −1/ 5,

lim

= −1/ 5,

y(0) = -1/5,

+ 4x −5

+4x −5

x→−0 x2

x→+0 x2

следовательно, функция в этой точке непрерывна.

Исследуем непрерывность функции в точке x3=1:

lim

= −∞,

lim

= ∞.

2 + 4x −5

+ 4x −5

x→1−0 x

x→1+0 x2

Следовательно, при х = 1 функция имеет разрыв второго.

Точки х = 1 и х = -5

являются вертикальными асимптотами.

5.8.Найти точки разрыва функции, если они существуют,

исделать чертеж:

, x ≤1;

, x ≤ −1;

а) y=

1, 1 < x ≤ 3;

б) y= x +1, −1 < x ≤ 0;

− x + 5, x > 3;

cos x, x > 0.

x = 0 и x = ±3;

2x −1, x < 0;

в) y=

9 − x2 , 0 <

≤ 3;

г) y=

, x ≥ 0.

> 3.

x −1

Решение. a) Функция неэлементарная, так как задана
тремя аналитическими выражениями на различных
промежутках изменения аргумента, определена на всем
множестве действительных чисел.					функции в точках х = 1 и
Исследуем	непрерывность					34
х = 3: y(1) = lim x2 =1;		y(3) =1;			lim (−x + 5) = 2 = k.

x→1−0					x→3+0
Таким образом, в точке х = 1 функция непрерывна, а в
точке х = 3 терпит разрыв первого рода (рис. 1.13) и имеет
скачок, равный	y(3) − k	=	1 − 2	=1.

Рис. 1.13

б) Функция определена на всем множестве чисел и неэлементарная.

Исследуем непрерывность функции в точках х = -1 и х = 0:

y(-1) =	1	,	lim (x +1) = 0; y(0) =1;	lim cos x =1.
	2
			x→−1+0	x→+0

Таким образом, функция в точке x = -1 имеет разрыв первого рода, а в точке х = 0 непрерывна (рис. 1.14).

Рис. 1.14

в) Функция определена на всей числовой оси, неэлементарная.

Исследуем непрерывность функции в точках х = - 3 , x=0, x= 3:

y(-3)=3,	lim	(9 − x2 ) = 0; y(−3 − 0) = 9;
	x→−3+0
y(0)=3,	lim (9 − x2 ) = 9; lim y(9 − x2 ) = 9;
	x→−0	x→+0
y(3)=3,	lim	(9 − x2 ) = 0; y(3 + 0) = 9.
	x→3−0

Таким образом, функция в точках х = -3 и х = 3 имеет разрывы первого рода, а в точке x = 0 устранимый разрыв

(рис. 1.15).

Рис.1.15

г) Функция неэлементарная и определена везде кроме точки x = 1. Исследуем непрерывность функции в точках х = 0

и х = 1:

lim (2x −1) = −1,	y(0) = −1, lim	1	= −∞, lim	1	= ∞.
		x −1		x −1
x→−0	x→−0		x→+0
Таким образом,	функция в точке х = 0 непрерывна, а в

точке х = 1 имеет разрыв второго рода (рис. 1.16).

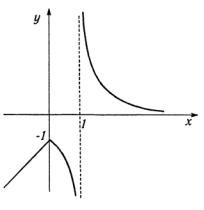
Рис. 1.16

5.9. Найти точки разрыва функции и построить график в

окрестности точек разрыва: а) f(x)=

x +1

; б ) f(x)=3

. .

x 2 −1

x2 − x − 2

Решение. а) Приравнивая знаменатель к нулю, находим

корни и преобразуем выражение

x +1

f(x)=

− x −

(x +

1)(x − 2)

Функция не определена в

точках

х = -1 и х = 2 и,

следовательно, имеет в этих точках разрывы. Находим односторонние пределы для точки х = -1:

1. При x→-1-0,

х + 1<0 и, следовательно, |х+1| = -(х+1).

Отсюда f(-1-0)=

lim

− (x +1)2

= −2

lim

(x +1)(x − 2)

x→−1−0

x→−1−0 x − 2

2. При x→-1+0

x+1>0,

x +1

= x +1

f(-1+0) = lim

2(x +1)

= 2 lim

= −

2 .

x→−1+0 (x +1)(x −2)

x→−1+0 x −2

Поскольку оба предела конечны и не равны, то точка х = -1

— точка разрыва первого рода. 39

Находим скачок функции (рис. 1.17)

δ= f (−1 + 0) − f (−1 −0) = − 23 − 23 = − 43 .

Вокрестности точки x=2 x+1>0 , следовательно, |х+1| = х+1 и односторонние пределы будут

f(2-0) =	lim	2(x +1)	= 2	lim	1	= −∞,
		(x +1)(x − 2)			x − 2
	x→2−0			x→2−0
f(2+0)=	lim	2(x +1)	= 2	lim	1	= ∞.
		(x +1)(x − 2)			x − 2
	x→2+0			x→2+0

Таким образом, точка х=2—точка разрыва второго рода.

Рис. 1.17

б) Данная показательная функция не определена в точках x= -1 и x= 1 и, следовательно, имеет в этих точках разрывы.

Найдем односторонние пределы, учитывая, что а > 1, то

есть a' →+∞ при

t=+∞ и a' →0 при t→-∞.

1. Для точки

х = -1 при

x→-1-0,

x2 – 1 > 0,

< 0

−1

→ −∞. Отсюда f(-1-0) =

lim 3

= 0.

x2 −1

x→−1−0

При x→-1+0,

x2-1<0,

< 0,

→ ∞.

x2 −1

2 −1

<<< < Предыдущая 1 2 34 / 234 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.77 Mб2Учебное пособие 1691.pdf
#
30.04.20221.78 Mб3Учебное пособие 1692.pdf
#
30.04.20221.79 Mб5Учебное пособие 1693.pdf
#
30.04.20221.79 Mб9Учебное пособие 1694.pdf
#
30.04.20221.79 Mб25Учебное пособие 1695.pdf
#
30.04.20221.8 Mб6Учебное пособие 1696.pdf
#
30.04.20221.8 Mб2Учебное пособие 1697.pdf
#
30.04.20221.8 Mб2Учебное пособие 1698.pdf
#
30.04.20221.81 Mб7Учебное пособие 1699.pdf
#
30.04.2022207.49 Кб6Учебное пособие 17.pdf
#
30.04.2022310.52 Кб19Учебное пособие 170.pdf