Учебное пособие 1696

тельно, кривая имеет горизонтальную асимптоту y = 0. При t →1: x →1; y → ∞ следовательно, кривая имеет вертикаль-

следовательно, наклонные асимптоты имеют вид y = x − 2e , y = −x + 21e .

в) Приведем уравнение заданное в полярных координа-

тах к параметрическому виду: x = a cosϕ ϕ , y = a sinϕ ϕ , где ϕ -

вательно, кривая имеет горизонтальную асимптоту у = а (рис. 2.52).

141

можно построить асимптоты и график функции (рис. 2.53).

Рис. 2.53

2.14. Исследование функции и построение графиков

При исследовании функции и построении ее графика рекомендуется примерная схема:

1. Определить область существования функции. Найти точки разрыва функции и односторонние пределы в точках разрыва.

2. Выяснить, не является ли функция периодической, четной или нечетной, т. е. не симметричен ли график относительно оси ординат или начала координат.

143

3.Найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.

4.Найти точки экстремума и интервалы возрастания и убывания функции. Определить значения функции в точках экстремума, если такие существуют.

5.Найти точки перегиба и интервалы выпуклости и вогнутости графика функции. Определить значения функции в точках перегиба.

6.Определить асимптоты функции.

7.Построить график функции, используя все полученные данные.

По мере построения графика бывает очевидным, какие вопросы исследования целесообразно опустить, а какие добавить.

Если данных для построения недостаточно, то следует найти еще несколько точек графика функции, исходя из ее уравнения. Результаты исследования функции целесообразно заносить сразу же на рисунок, тогда к концу проведения исследования график будет практически построен.

14.1.Исследовать функции и построить их графики:

Решение. а) Областью существования функции является вся числовая ось. Функция четная, следовательно, график функции симметричен относительно оси ординат.

Полагая x = 0, находим точку пресечения графика с осью ординат у = -9.

Приведем функцию к виду y = (x2 +1)(x2 −9) , тогда, решая уравнение (x2 +1)(x2 −9) =0, точки пересечения с осью абсцисс будут x = ±3 .

144

Находим производную y′ = 4x3 −16x и приравниваем ее к нулю 4x3 −16x =0. Из решения уравнения x(x2 − 4) = 0 находим критические точки x1 = 0, x2 = 2, x3 = −2 . Находим вторую производную y′′ = −12x2 −16 . Так как y′′(±2) > 0 , то точ-

ки x2=2 и x3 = -2 есть точки минимума функции, а так как y′′(0) = 0 , то точка x = 0 есть точка максимума. Значения

функции в экстремальных точках равны: y(0) = -9; y(±2) = -25. Чтобы отыскать возможные точки перегиба, решаем

уравнение: y′′ = 0; 12х2 -16 = 0, откуда x = ± 23 . Так как y′′

меняет свой знак при переходе через эти точки, то при этих значениях х график функции имеет перегиб. Находим ордина-

При неограниченном возрастании х по абсолютной вели-

График функции показан на рис. 2.54.

Рис. 2.54

145

б) Функция существует всюду, кроме точек х = ± 3 .

Прямые x = 3 и x = − 3 являются вертикальными асимптотами функции. Найдем односторонние пределы в точках разрыва

Функция нечетна, следовательно, ее график симметричен относительно начала координат. При х = 0 имеем y = 0, следовательно, график функции проходит через начало координат.

x1 = −3, x2 = 0, x3 = 3 .

Рассмотрим методом интервалов изменение знака y′при

переходе через эти точки (рис. 2.55 ). Следовательно, в точке x = −3 функция имеет минимум y(−3) = 4,5, а в точке х = 3

имеет максимум y(3) = 4,5 . При переходе через х = 0 произ-

водная знака не меняет, следовательно, в точке х = 0 экстремума нет.

производная y′′=0 при х = 0 и меняет знак с минуса на плюс

146

при переходе через эту точку, следовательно, и точка х = 0 есть точка перегиба.

Находим асимптоты кривой:

следовательно, кривая имеет наклонную асимптоту y = −x . График функции показан на рис.2.56.

Рис. 2.56

в) Находим область существования функции. Функция существует при xx −+12 >0, т. е. при x ] − ∞,−1[ и x ]2, ∞[ (рис. 2.57).

147

не обращается в нуль ни при каком значении х, значит экстремумов нет.

кривая выпукла вниз; при х > 2 имеем у" <0 - кривая выпукла вверх.

тальная асимптота. График функции показан на рис. 2.58.

Рис. 2.58

г) Областью существования функции является вся числовая ось. При x = 0 функция равна нулю. Так как x2 ≥ 0, и e−x > 0 , то y ≥ 0 при любом x.

148

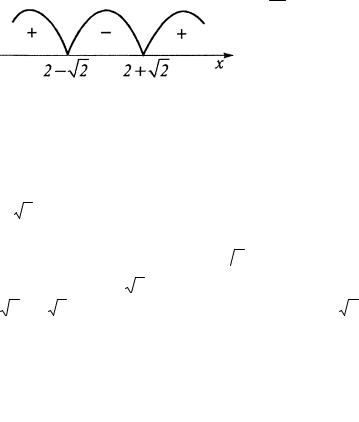
Находим производную y′ = xe−x (2 − x) и приравниваем ее к нулю xe−x (2 − x) = 0 .

Решая это уравнение, находим критические точки х1=0 и x2 = 2. Поскольку производная меняет знак согласно схеме (рис. 2.59), то в точке x = 0 функция имеет максимум, равный

нулю, а в точке х = 2 минимум, равный y(2) = e42 ,

схеме (рис. 2.60), то в точках x1,2 = 2 ± 2 функция имеет пе-

Рис. 2.60

149

т. е. прямая у = 0 есть горизонтальная асимптота. График функции показан на рис. 2.61.

Рис. 2.61

д) Функция существует для всех значений х, кроме х = 1. При x = 1 функция терпит разрыв. При х = 0 функция равна нулю. При x ≠ 0 имеем y > 0, т. е. функция не отрица-

знак с минуса на плюс при переходе через эту точку, следова-

150