Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1696

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.8 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 235 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Следовательно, f(- 1+0) = lim 3x 2 −1 = +∞ .

x→−1+0

Таким образом, точка х = -1 —точка разрыва второго рода.

2. Рассмотрим точку х = 1. Находим пределы

	x			x
f(1 - 0) = lim 3	x 2 −1	= 0,	f(1 + 0) = lim 3	x 2 −1	= +∞,
x→1−0			x→1+0

функция в точке х = 1 имеет также разрыв второго рода.

Найдем теперь пределы при			х → ± ∞ .
	x			x
f (-∞) = lim 3	x2 −1	=1, f (∞) =	lim 3x2 −1		=1 .
x→−∞			x→+∞

График функции показан на рис. 1.18.

Рис. 1.18

2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 2.1. Вычисление производных

10. Производной от функции у = f (x) в точке x 0 называется предел отношения приращения функции к приращению аргумента

lim

f (x0

+ x) − f (x)

= lim

x →0

Если этот предел конечный, то функция называется

дифференцируемой в точке x 0.

Производная обычно обозначается y‘

или

yx’ , или f’‘(x),

или

Нахождение

производной

называется

дифференцированием функции.

x = a

Частное

значение

производной при

обозначается

f ‘(a)

или y ‘ x = a.

Геометрически производная y‘(x0)

функции y = f(х)

представляет

угловой

коэффициент

k = tgα = y‘(x0)

касательной к графику этой функции в точке х0 (рис.2.1).

Рис. 2.1

Числа

f '

(x ) = lim

y(x0 )

f '

(x ) = lim

y(x0 )

−

x→−0

x→+0

называются

соответственно

левой

правой

производными

lim

x→0+

функции у = f(x) в точке x0 . Для существования производной функции f (х) в точке x0 необходимо и достаточно, чтобы ее левая и правая производные в этой точке существовали и были равны между собой: f−' (x0 ) = f+' (x0 ) .

Если существует (конечный или нет) предел

lim	f (x) = M , то такова же будет и производная в точке x0
x→x0 ±0
справа (слева).
Если в точке x0 производная не определена, но функция
имеет	различные односторонние пределы lim	y(x0 )	и
	x→0−	x

y(x0 ) , то в этой точке графика функции существуют две x

различные с соответствующими угловыми коэффициентами k 1 , k 2 односторонние касательные, составляющие угол (рис. 2.2), а точка называется угловой.

			Рис. 2.2
Если	lim	y(x1)	= ±∞, то есть функция имеет
	x→0	x

бесконечную производную, то она не дифференцируема в этой точке. В этом случае график функции имеет вертикальную касательную (точка перегиба).

Если в точке x2	функция	имеет	бесконечные
односторонние производные	разных	знаков,	то график

функции имеет две слившиеся вертикальные касательные (точка возврата с вертикальной касательной (рис. 2.2)).

20. Основные правила дифференцирования:

1. (Cu)’=Cu’;

2. (u+v)’ = u’ + v’ ;

3. (uv)’ =u'v + v'u;

u'v −uv'

где u ,v — некоторые функции от x, a С - постоянная

величина.

30. Таблица производных основных функций:

1. (xn)’=nxn-1;

2. y = C, y’= 0;

3. (sin x)’= cos x ;

4. (cos x)’= - sin x;

5. (tg x)’ =

;

(ctg x)’ = -

;

cos2 x

sin2 x

7. (ax)’ = ax lna, a>0;

(ex)’ = ex;

’

9. (logax) =

, a≠1, a>0;

10.

(ln x) =

;

x ln a

11. (arcsin x)’=

; 12. (arcos x)’ = -

;

1 − x2

13. (arctg x)’ =

;

14. (arcctg x)’ = -

;

+ x2

1 + x2

16. (ch x)’ = sh x;

15. (sh x)’ = ch x;

17. (th)’ =

;

18. (ctg x)’ = -

;

ch x

40. Гиперболический синус, косинус, тангенс и котангенс

определяются выражениями

sh x=

− e−x

; ch x =

ex + e−x

; th x =

shx

; cth x =

chx

shx

обладают свойствами:

1. ch2 x – sh 2x =1;

2. ch2 x – sh 2x = ch2x;

3. sh2x = 2shxchx;

sh0 = 0;

ch0 = l.

50. Производная от сложной функции y = f(u), где u = u(х), равна произведению производной от этой функции по промежуточному аргументу и на производную от

промежуточного аргумента и по независимой переменной х,

т. е. y’ = f ’u u’x .

1.1. Пользуясь только определением производной, найти

производные от функций:
а) у=х2 - Зх + 5; 6) у =					x ; в) y = tg2x.
Решение. а) Находим приращение функции
y = y(x+			x) – y = (x +		x)2 – 3(x+		x) + 5 – x2 +3x -5= x2 +
2x x +	x2 – 3x -3 x+5 - x2 +3x -5 = 2x						x + x2 - 3 x.
По определению производной имеем
’	lim	y	lim	2x x +	x2 −3 x	=

y =	x→0	x = x→0			x

= lim (2x −3 + x)= 2x −3.

x→0

б) Приращение функции равно:

x +

x −

x .

По определению производной имеем:

у‘ = lim

y = lim

x +

x −

x =

x→0

= lim ( x +

x −

x )( x +

x +

x ) =

x→0

x +

x )

= lim

x + x − x

= lim

x )

1 .

x→0

x( x + x +

x )

x→0 ( x + x +

2 x

в) Находим приращение функции

y = tg(2x + 2

x) - tg2x =

sin(2x + 2

x) cos 2x −sin 2x cos(2x + 2

cos(2x + 2 x) cos 2x

sin(2

cos(2x + 2

x)cos 2x

По определению производной

= lim

sin(2

x cos(2x + 2 x) cos 2x

x→0

= lim

x)cos 2x

cos2 2x

x→0 cos(2x + 2

1.2. Найти производные функций:

а) y = |х|, (х ≠ 0); б) y = |2х-3|; в) y = e2 x ;

г) y = |х + 1| + |х - 1 | .

Решение. а) Представим функцию в виде

x, x > 0;

y =

x < 0;

тогда

− x,

1, x > 0;

y' =

−1, x < 0.

Следует

заметить,

что

функция

у = x

производной

точке

x0, так

как

f−' (0) = lim −

x→−0

f+' (0) = lim

=1.

x→+0

б) Представим функцию в виде

2x −3,

x > 0;

y =

+3,

x < 0,

− 2x

тогда

2, x

;

x <

− 2,

в) Представим функцию в виде

2 x

x > 0;

y =

−2 x

x < 0.

не имеет xx = −1 , а

В этом случае производная будет

2 x

x > 0;

2 x

− 2e

, x < 0.

г) Представим функцию в виде

2x,

x >1;

y =

−1 < x <1;

x < −1,

− 2x,

тогда

x >1;

0, −1 < x <1;

x < −1.

− 2,

y-‘(x0),

y+’(x0)

1.3. Найти производные

для функций:

а)

y =

x ≤1;

x0 = 1;

+ 2x, x >

− x2

б) y = 1 − e−x 2 , x = 0;

в) y =

2 − x

2 + x

, x0 = ±2.

Решение. а) Находим производную

x ≤1;

x >1

− 2x + 2,

и вычислим пределы производной слева и справа в точке

x0=1:

y−′(1) = lim 1 =1,

y+′ = lim (−2x + 2) = 0.

x→1−0

x→1+0

б)

Находим производную y'

и вычислим

ex 2

1 − e−x 2

пределы производной слева и справа в точке x0:

y−′(0) = lim

= −1,

ex2

→−0

ex2 −1

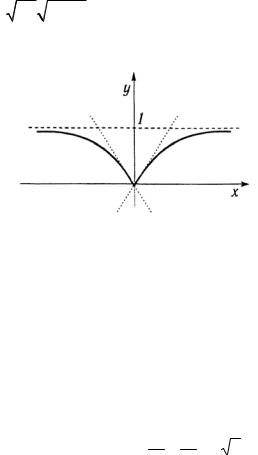
y+′(0) = lim	x	=1.
	ex2 −1
x→+0 ex2

Касательные к кривой в точке x0 = 0 показаны на рис. 2.3.

Рис. 2.3

в) Представим заданную функцию в виде

− 2x, x ]− ∞,−2];

y = 0, x ]− 2,2];

2x, x ]2,∞[

и найдём производную

− 2, x ]− ∞,−2];

y′ = 0, x ]− 2,2];

2, x ]2,∞[.

1.4. Найти производные: а) y =

−

+ 4 x −5

;

+1,

б) y = x cos x; в) y

; г) y =

− x

x2 +1

′

вычислить f (0),

(1),

(−1).

Решение. а) Преобразуем функцию к виду, удобному для дифференцирования. Пользуясь основными правилами дифференцирования и таблицей производных, имеем

= 1 x3 −

3x−2 + 4x2 −5,

−3

−

y′ = 2 x

+6x

+ 2x

2 =

2 x

б) Здесь имеет место случай произведения двух функций,

поэтому

′

= 3x

cos x − x

sin x.

) cos x + x

(cos x)

в) Поскольку имеет место частное двух функций, то

′

+1) − (x

)(x

′

+ 2x − 2x

) (x

+1)

(x2 +1)2

г) Находим производную f'{x) = x2 - 2х и вычисляем ее значения в точках x = 0, х = 1, х = - 1 , т. е. находим частные значения производной в этих точках:

f	′	= 0,	f	′	= −1,	f	′	= 3.
	(0)			(1)			(−1)

1.5.Найти производные: а) y = ln x2 − 4x + 4 ;

x2 + 4x + 4

б)

y = ln

x +1

;

в)

y = log2

3 tg 2 2x;

x2 − x +

г)

y = ln3 cos

Решение. a) Упростим логарифмируемое выражение

x − 2

y = ln

= 2ln

Полагая у = 2ln и,

u =

x + 2

применяем правило дифференцирования сложной функции

y′ = 2(ln u)′u u′x = 2

x + 2

(x − 2)′(x + 2) − (x − 2)(x + 2)′

x − 2

− 4

(x + 2)2

б) Полагая у = lп и, где и =	x +1	, имеем
б) Полагая у = lп и, где и =	x2 − x +1	, имеем
y′ = 2(ln u)′u u′x =

x2 − x +1 − (x +1)

2x −1

x2 − x +1

2 x2 − x +1

x +1

x2 − x +1

1 − x

3 1 − x

2 (x +1)(x2 − x +1)

2 (x +1)3

в) Упростим логарифмируемое выражение

y = log2 tg

2x =

log2 tg2x.

Дифференцируем как сложную функцию

y′ = 3

= 3

tg2x ln 2

cos2 2x

sin 4x ln 2

г) Дифференцируем как сложную функцию

′

= 3ln

cos 3 cos

(−sin 3) 3 = −tg 3 ln

cos 3 .

−

1.6. Найти производные: а) z = xea

+ ae

a ;

б)

y = e−3x (sin 3x + cos3x) ; в) z = ln

1 − 2x

;

1 + 2x

г) y = esin 3

x + 55

x .

Решение.

Дифференцируем

−

функций z′ = ea + xea

+ ae

−

как сумму сложных eax 1+ ax −e−ax .

б) Дифференцируем как произведение сложных функций y′ = e−3x (−3)(sin 3x + cos3x) + e−3x (cos3x 3 + (−sin 3x) 3) =

= −6e−3x sin 3x.

в) Упростим функцию y = 1 ln 1 − 2x . 2 1 + 2x

Находим производную как от сложной функции

<<< < Предыдущая 1 2 3 45 / 235 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.77 Mб2Учебное пособие 1691.pdf
#
30.04.20221.78 Mб3Учебное пособие 1692.pdf
#
30.04.20221.79 Mб5Учебное пособие 1693.pdf
#
30.04.20221.79 Mб9Учебное пособие 1694.pdf
#
30.04.20221.79 Mб25Учебное пособие 1695.pdf
#
30.04.20221.8 Mб6Учебное пособие 1696.pdf
#
30.04.20221.8 Mб2Учебное пособие 1697.pdf
#
30.04.20221.8 Mб2Учебное пособие 1698.pdf
#
30.04.20221.81 Mб7Учебное пособие 1699.pdf
#
30.04.2022207.49 Кб6Учебное пособие 17.pdf
#
30.04.2022310.52 Кб19Учебное пособие 170.pdf