Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1684

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

Y = C S

min

C S g

t .

Так как G = Y = Cy S

min

то

G - Y =

Gt .

Vmin Cy

С другой

стороны

G - Y = m

dVy

Следовательно,

dVy

2g2

t .

Vmin Cy

Интегрируя равенство

от

до

и от

0 до t получим,

что

t2 .

Vmin Cy

С другой

стороны

dH Vy dt ,

Следовательно,

	dH		g2		Cx		t2 .
							t2 .
	dt		Vmin Cy
Интегрируя от 0 до H и		от		0 до t получим, что
	H =		g2		Cx	t3 .
	H =					t3 .
		3Vmin Cy

Из последнего равенства следует, что время парашют и- рования самолета с заданной высоты равно:

t = 3	3HVminCy	.

	g2Cx
Подставляя время t в уравнение (*),			получим формулу
для определения посадочной скорости			самолета

3Hg

Vпос

Vmin 1

Vmin2

Пусть высота парашютирования H=0,7 м ,

K = 5 ,

Vmi n=

60 м / с. Тогда из последнего

равенс тва следует,

что

Vпос

0,94Vmin

или

Vпос

0,94

SCy max

Обычно последняя

формула

используется

для определ е-

ния в первом приближении посадочной скорости сам оле-

тов

всех типов.

5. При

пробеге

на самолет действуют те же силы,

что и при разбеге.

Поэтому, произведя те же выкладки,

что

и при

расчете

разбега, получим

для

случая проб ега

самолета следующее

уравнение

1 dV

S V2

fпр

fпрCy

g dt G

где fпр - коэффициент трения колес самолета о пос адочную полосу при пробег е с учетом работы тормо зной системы.

Произведя в последнем	равенстве замену	переме нных
и выполнив интегрирование	от 0 до Lпр и	от V2	пос до
0, получим, что

1 Lпр 2g

V	2					2
пос				dV
				dV					.
					SV2				.
	0	Cx	fпрCy		SV2		fпр	P
		Cx	fпрCy		2G		fпр	G
					2G			G

Из полученного равенства видно, что уменьшение длины пробега можно достичь за счет увеличения коэффициента трения колес о посадочную полосу, за счет применения реверса тяги, за счет увеличения коэффициента лобового сопротивления самолета и за счет уменьшения посадочной скорости. Посадочную скорость можно уменьшить за счет увеличения Сy max . Для увеличения Сy max применяют закрылки. Так как при посадке

дополнительное сопротивление играет полож ительную роль, то закрылки в этом случае отклоняют на макс и- мально возможный угол. Кроме этого для ув еличения Сx при посадке применяют тормозные щитки, тормозные п а- рашюты и т.д.

5. Неустановившееся движение самолета в вертикальной плоскости

5.1. Динамический потолок самолета

Неустановившееся движение в отличии от кв азиустановившегося характеризуется значительным изм енением кинематических параметров.

Одним из характерных примеров неустановившег ося движения является выход самолета на динамический п о- толок.

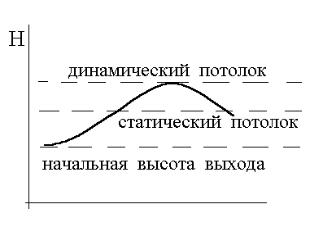
Под динамическим потолком самолета понимается предельно достижимая высота полета, причем на этой высоте на движение самолета не накладывается ник аких ограничений, кроме требования безопасности полета (рис.

5.1).

Рис. 5.1

Выход на динамический потолок достигается за счет превращения части кинетической энергии самолета в п о- тенциальную. При этом происходит уменьшение ск орости полета и соответственно скоростного напора. При очень маленьких значениях скоростного напора аэродинамич е-

ские силы также оказываются очень м алыми и самолет становится неуправляем.

Поэтому под динамическим потолком понимается т а- кая предельная высота полета, на которой сохраняе тся

допустимый по	условиям	безопасн	ости	скоростной		напор
q без . Очевидно,	что при	заданном	значении		q без	высота
динамического	потолка	получится		тем	больше, чем

больше удельный запас полной энергии самолета в м о- мент выхода на динамический потолок.

Очевидно, что на каждой высоте наибольшей удел ь- ной энергией самолет будет обладать при макс имальной скорости полета.

Таким образом, выход на динамический потолок в ы- полняется при максимальной скорости полета с т акой высоты, на которой самолет обладает наибольшей удельной энергией, равно

Hэ max H 2gmax .

Определить эту высоту можно следующим образом. Пользуясь методом тяг или мощностей строят гр а-

фики зависимости максимальной скорости горизонтал ьно-

го	полета	от высоты Vmax = Vmax (H)				(рис. 5.2). На этот
же	график	наносят	кривые	Hэ = const		по уравнению
			H	Hэ	V2
			H	Hэ	2g
					2g
Рядом значений Hэ			задаются.
	Очевидно, что		точка	касания кривых Vmax (H) и

Hэ=const определит начальную высоту выхода на динамический потолок H1 , максимальную скорость гор изон-

тального полета на этой			высоте Vmax 1 и полную удель-
ную энергию	самолета	в	начальный момент выхода на
динамический	потолок	Hэ 1 .

Удельный запас энергии самолета на динамическом п о- толке Hд отличается от удельного запаса энергии с амолета на начальной высоте на величину работы внешних

			Рис. 5.2
сил на пути S.
Hэд	Hд	Vд2	Hэ1	1	(P Q)dS .
Hэд	Hд	2q	Hэ1	G S	(P Q)dS .
		2q		G S

Величина работы внешних сил при выходе самолета на динамический потолок имеет отрицательное значение и зависит от закона управления самолетом.

Таким образом, задача об определении динамич еского потолка самолета предполагает кроме определ ения начальной высоты выхода на динамический пот олок, определение такого закона управления самолетом, при кот о- ром работа внешних сил имеет минимальное значение.

Решение задачи в	такой постановке				дано	в 6 .
Ограничимся	приближенной			оценкой		динамического
потолка самолета.	Обозначим
	1		(P Q)dS	Hэ1 .

		G S
		G S
С учетом принятого обозначения					выражение для Hэ д
примет вид:

			V2
	Hэд	Hд	д	Hэ1	(1	).
	Hэд	Hд	2q	Hэ1	(1	).
			2q
Так как Hэ 1 величина		известная, то,				задаваясь	рядом зн а-
чений	, можно построить		кривые		(рис. 5.3)		Hэ д =
const	по уравнению

			Рис. 5.3
							V2
		Hд Hэ1(1 )					д	.
		Hд Hэ1(1 )						.
							2q
На	эти	же кривые наносят график зависимости H=H(V)
по	уравнению
					2qбез
					V2
или
		pH			qбез	.
		pH		0,7 M2		.
				0,7 M2
Очевидно, что точки пересечения							кривых		Hэ д = const и
кривой H=H(V) дадут значения динамического потолка
самолета		при разных значениях				, т.е. при			разных допу-

щениях о величине работы внешних сил при выходе с а- молета на динамический потолок.

	5.2. Уравнения		неустановившегося движения
			самолета
	Силы,	действующие на самолет в вертикальной
плоскости,		приведены	на рис. 5.4 при условии, что
	с с	0.
	с с

Проектируя силы на оси скоростной системы коорд инат, получим следующие уравнения неустановившегося дв и- жения самолета в вертикальной плоскости

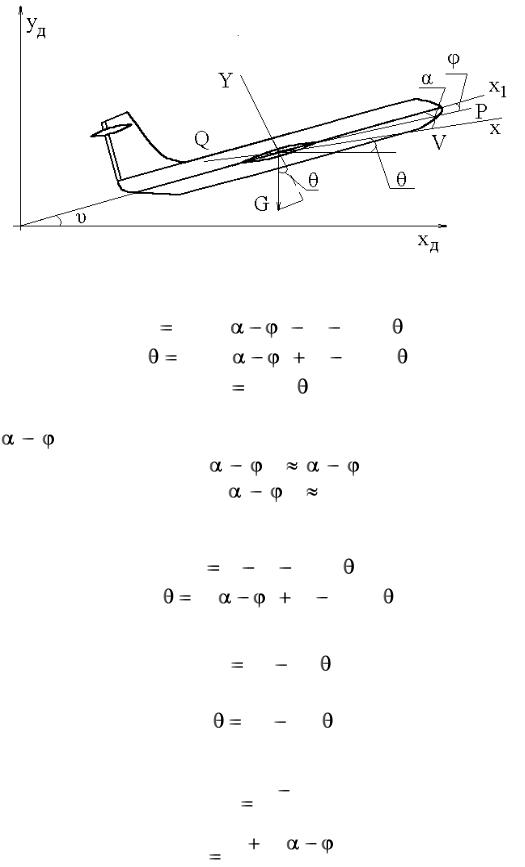
Рис. 5.4

	mV	P cos(	)	Q	G sin

	mV	P sin(	)	Y	G cos
		H	V sin .

Так	как при полетах		в плотных слоях атмосферы
угол	мал, то	можно	принять, что
		sin (	)
		cos (		)	1.

С учетом принятых допущений уравнения движения с а-

молета принимают вид:					Q		G sin
mV P					Q		G sin

mV P(						)	Y G cos
или
		1
			V		nx		sin
		g
	V				n		cos
		g			n	y	cos
						y

где
			nx			P	Q

						G
						G
ny				Y		P(	)

						G
						G

К трем рассмотренным уравнениям часто добавляют сл е- дующие кинематические соотношения

L	V cos

Итак, полагая, что законы	изменения	P=P(t), m=m(t) и
зависимости Сy= Сy( , M)	и Cx =Сx (Сy , M) известны, име-
ем 5 уравнений с 6 неизвестными V,		H, , , , L.
Для однозначного решения этой		системы 5 ура вне-

ний необходимо задаться законом изменения одной из 6 переменных. Чаще всего задаются законом изм енения одной из следующих величин ny (t), (t), (t).

Взависимости от характера задания закона изм енения лишнего неизвестного все траектории движения с а- молета можно разделить на траектории программного движения и траектории наведения.

Вслучае траекторий программного движения закон изменения лишнего неизвестного задается в виде опр е- деленной заранее известной функции.

Вслучае траекторий наведения закон изменения лишней переменной заранее неизвестен и должен быть

найден из условия принятого метода наведения сам оле- та-перехватчика.

Итак, неустановившееся движение самолета в ве ртикальной плоскости описывается системой из 6 ура внений с 6 неизвестными. Эти уравнения являются н елинейными дифференциальными уравнениями, не име ющими аналитических методов решения. Для решения этих уравнений в частных случаях разработаны ра зличные численные методы 6 . Кроме этого, решение этих уравнений при л ю- бом характере задания лишнего неизвестного можно п о- лучить путем численного интегрирования.

5.3. Методы численного интегрирования дифференциальных уравнений

Существует много методов численного интегрир ования дифференциальных уравнений. Ограничимся ра ссмот-

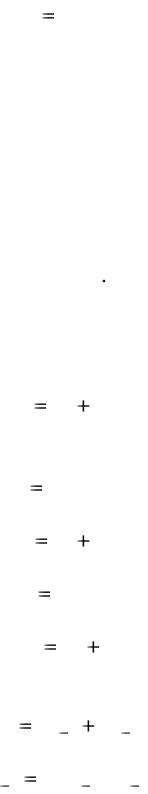
рением лишь тех из них, которые получили наиб олее широкое применение в динамике полета самолета.

1. Метод Эйлера Рассмотрим задачу интегрирования одного дифф е-

ренциального уравнения первого порядка.

Это уравнение имеет вид:

y f (x, y)

где x - независимая переменная и y(x) - искомая функция. Будем искать решение, удовлетворяющее начальному у с- ловию:

y( x0 )=y0 .

Это так называемая задача с начальными условиями, к о- торая иначе называется задачей Коши.

Разобьем интервал интегрирования (x-x0) на достаточно большое число участков n, достаточно малой про-

тяженности h, так что
x - x0 = n	h .
Сущность метода Эйлера	состоит в том, что на к а-

ждом из участков искомая зависимость y(x) принимается линейной.

В этом случае для первого участка имеем

y1	y0	y0h .
Значение производной y0	на	первом	участке находится
по заданному уравнению и	начальным		условиям, т.е.
y0	f (x0, y0 ) .

Аналогично, для второго участка имеем, что

y2 y1 y1h ,

где

y1	f (x1, y1 )
и
x1	x0 h .

Таким образом, в соответствии с методом Эйлера зн аче-

ние функции на n-и ном	участке	интегрирования равно
yn	yn 1 yn	1h
где
yn 1	f (xn 1, yn 1 ).

Аналогично применяется метод Эйлера и для решения системы дифференциальных уравнений.

2. Метод средней ординаты Рассмотренный метод Эйлера является весьма пр о-

стым методом численного интегрирования и в этом его достоинство. Однако результаты расчетов при пр именении метода Эйлера получаются с достаточно большой погрешностью. Причем, основная погрешность при инте г-

рировании по методу	Эйлера		получается	вследствие т о-
го, что производной	y на	всем	участке h	приписывается
ее значение в начале этого участка.
Погрешность метода		Эйлера можно существенно

уменьшить, если вместо значения производной в начале участка интегрирования принять ее среднее значение на

этом	участке.	В этом и состоит сущность метода сре д-
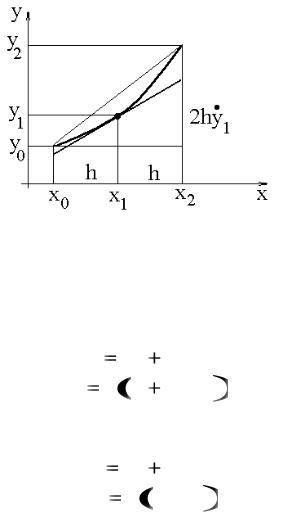
ней	ординаты	(рис. 5.5).

Рис. 5.5

Таким образом, при использовании метода средней ординаты значение функции в конце второго участка интегрирования равно

	y2	y0	2hy1 ,
где	y1	f x0	h, y1 .

Аналогично, значение функции в конце третьего участка

интегрирования	равно
	y3	y1	2hy2 ,
где	y2	f	x2, y2 .

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022310.11 Кб2Учебное пособие 168.pdf
#
30.04.20221.74 Mб6Учебное пособие 1680.pdf
#
30.04.20221.74 Mб2Учебное пособие 1681.pdf
#
30.04.20221.74 Mб4Учебное пособие 1682.pdf
#
30.04.20221.75 Mб3Учебное пособие 1683.pdf
#
30.04.20221.75 Mб38Учебное пособие 1684.pdf
#
30.04.20221.76 Mб3Учебное пособие 1685.pdf
#
30.04.20221.76 Mб4Учебное пособие 1686.pdf
#
30.04.20221.76 Mб3Учебное пособие 1687.pdf
#
30.04.20221.76 Mб3Учебное пособие 1688.pdf
#
30.04.20221.76 Mб2Учебное пособие 1689.pdf