Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Динамика полета. расчет траекторий самолетов, учебное пособие. Пентюхов В.И., Будник А.П

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

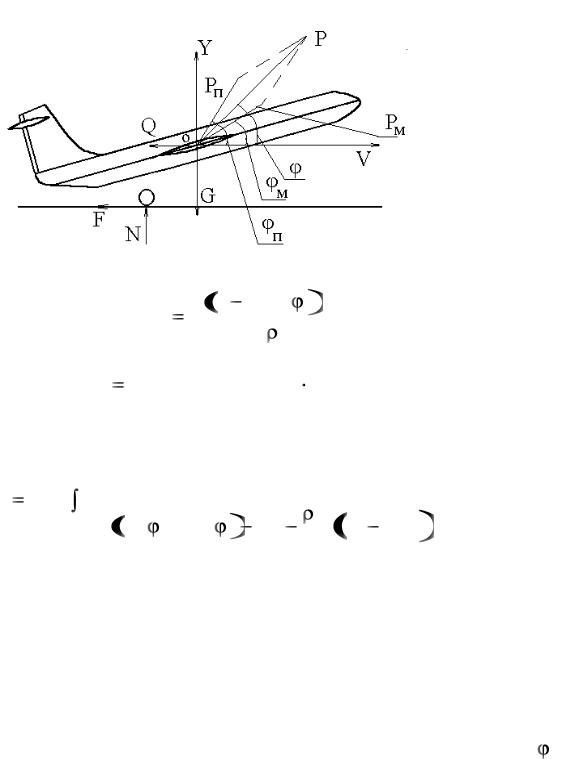
Рис. 4.3

		V2		2 G	P sin	.


			отр	Cy отр S
				Cy отр S
Учитывая, что	dV		1 dV2	и	F = f N, после совместного

	dt		2 dL
	dt		2 dL

решения уравнений получим следующие выражение для длины разбега самолета:

1 Vот2

GdV2

2g 0

P cos + fsin

Предположим, что при разбеге самолета справедливы

следующие допущения:
1)	вес самолета не меняется;
2)	угол атаки остается постоянным, т.е. Сy=const;	Сx =
const;
3)	коэффициент трения f =const;
4)	тяга двигателей не зависит от скорости, т.е. P=const;
5)	направление полного вектора тяги не меняется, т.е.
=const .
	Эти допущения вносят некоторую погрешность в
определение длины разбега самолета, однако в этом		сл у-

чае интеграл, входящий в формулу для длины ра збега легко вычисляется аналитически, так что

L	G		ln		P cos + fsin		fG	.

	g S Cx	fCy		P cos	+ fsin fG	Cx	fCy G P sin
	g S Cx	fCy				Cx	fCy G P sin
							Cy отр
							Cy отр

Из последнего равенства следует, что величина полного вектора тяги, потребная для обеспечения заданной дл ины разбега, равна:

	G f	f	Cx fCy		e	g SL Cx		fCy /G
P			Cy отр							( ).

				Cx	fCy
	cos + fsin	cos	f				sin	e	g SL Cx fCy /G
				Cy отр

Оптимальное направление полного вектора тяги может быть найдено из необходимого условия экстремума функции P = P ( ), которым как известно является у сло-

вие

опт

0 . Из этого

условия

следует, что

G f f

fCy

g SL Cx

fCy /G

Cy отр

( ) .

опт

g SL Cx

fCy

Достаточным

условием

минимума

функции P = P ( )

яв-

ляется условие

опт

которое

выполняется

при

любых характеристиках самолетов и условиях разбега не противоречащим принятым допущен иям.

Действительно, из равенства (*) следует, что

	2P	P ,

2
		опт
где P = OP есть величина		положительная. Следовател ьно,

равенство (*) действительно определяет оптимальное направление полного вектора тяги.

При значениях (Сх - fСу), близких к нулю, использовать непосредственное равенства (*) и (**) затруднительно,

так как пределами этих равенств при	(Сх - fСу)	0 яв-
ляются неопределенности типа 0/0.
Применяя к () и (*) правило	Лопиталя, получим,
что

G G fCy отр g SL

;

Cx fCy

Gsin

+ C

y отр

g SL cos

f sin

fCy отр g SL

опт

fCy 0

Cy отр g SL

Полученные равенства можно использовать для о п-

ределения величины и оптимального направления

по лно-

го

вектора тяги

обеспечивающего заданную д лину разбе-

га

самолета, при значениях (Сх - fСу) близких к нулю.

Если величина и направление вектора тяги

марш е-

вых

двигателей

известны, то можно определить велич ину

и направление

вектора тяги подъемных двигателей.

Действительно,

OPn= OP - OPм ,

где

величина

направление

полного вектора тяги о пре-

деляется согласно (*) и (**) или из последних равенств. Возведя в квадрат, получим, что

P2	P2	P2
			2PP	cos	м	,
n		м	м
где Pn = OPn ;	Pм =		OPм	; P =	OP .

Из предпоследнего выражения следует, что при зада нной величине тяги маршевых двигателей величина тяги подъемных двигателей, обеспечивающая заданную длину

разбега будет	минимальна в том случае, когда векторы
OPn , OPм , OP	коллинеарны. В этом случае Pn = P - Pм .

Однако, если принять во внимание ряд других усл овий, например, условие обеспечения продольного уск орения самолета при отрыве, то обеспечение коллинеа рности векторов OPм и OP может оказаться нецелесообразным.

Считая направление вектора тяги маршевых двиг ателей заданными и отличным от направления полного ве к-

тора тяги, найдем направление вектора тяги под ъемных двигателей.

Проектируя выражение для маршевого двигателя на ось x, получим, что

	Pn cos n		P cos	Pм cos	м ,
или
cos		P cos		Pм cos м		.
	n
		P2	P2	2PP cos
					м

			м	м

Очевидно, что	значение	угла n св в	связанной	с самоле-
том системе	координат	отличается	от значения	угла n,

определяемого последним равенством на величину угла атаки самолета при разбеге.

4.5. Об оптимизации режима разгона СВВП от нулевой до эволютивной скорости

Для самолетов вертикального взлета и посадки (СВВП) важное значение имеет экономия расхода то плива на переходных режимах полета. В этой связи представляет интерес задача об оптимальном векторе управления, т.е. определение оптимальных законов управления величиной и направлением вектора тяги силовой установки, из у с- ловия минимального расхода топлива.

Решение классическими вариационными методами такой задачи в общем случае приводит к необходим ости интегрирования на ЭВМ большого количества диффере н- циальных уравнений методом «пристрелки». Труд оемкость таких расчетов очень велика.

Вследствие этого, на этапе предварительного пр оектирования, когда параметры самолета еще точно не о п- ределены, целесообразнее провести приближенные расч е- ты.

Ниже рассматривается разгон СВВП от нулевой до эволютивной скорости по прямолинейной трае ктории

= const в вертикальной плоскости. Считаются спр аведливыми все допущения, применяемые для самолетов, сове р-

шающие полеты с умеренными скоростями ( M < 5) в атмосфере Земли. Кроме того предполагается, что расход топлива силовой установки qc пропорционален величине результирующей тяги P.

Последнее допущение вполне оправдано, поскольку для многих реактивных двигателей в довольно бол ьшом диапазоне тяг кривую q0 = (P) можно заменить прямой:

qc = qc o + kP ,

где k dqc . dP

С учетом принятых предположений движение самолета описывается следующими уравнениями:

gCx (H)V2S

0 ;

sin(

)

g sin

sin(

)

gCy (H)VS

sin

0 ;

qco

;

V cos

;

V sin

где

- угол

поворота

вектора тяги относительно ве рти-

кали к поверхности Земли;

L - горизонтальная

дальность;

H - высота полета.

Точка над буквой означает дифференцирование по вр е- мени t, остальные обозначения общепринятые .

Если горизонтальная дальность и высота, при к ото-

рых самолет достигает		скорости V = Vэв не регламенти-
руется, то два	последних уравнения можно		не учитывать
и оптимальная	задача	формулируется сл е	дующим обра-

зом: в классе допустимых кусочно - гладких функций определить оптимальный закон управления вектором тяги P (t), обеспечивающий минимум интегральной характери-

стики или, иначе, доставляющий	минимум функционалу
	t1
J G1 G0 qсо(t1	t0 ) k Pdt .
	t0

Здесь индекс «0» соответствуе т началу разгона, «1» - мо-

менту времени,

когда V = Vэв .

Преобразуем уравнения движения к следующему

в и-

ду:

gCx

V2S

G sin ;

P sin(

)

P cos(

)

G cos

gCy V2S

Исключив

из

этих

равенств

угол

получим

следующие

выражение

для

подынтегральной

функции

gCx V2S

gCy V2S

G sin

G cos

Функцию P с некоторым приближением можно считать

функцией

лишь

независимой

переменной

и скорости

V, если принять, что за время

взлета и

разгона

общий

вес самолета

меняется

незначительно,

т.е.

положить

G0 = const .

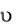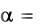
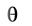
Естественно также предположить, что для удобства п илотирования угол тангажа должен быть постоянным, и поскольку в рассматриваемом случае = const, то угол атаки = const и лежит, по видимому в диапазоне наивыгоднейших углов атаки. Тогда необх одимым условием достижения минимума функционала является удо в- летворение подынтегральной функции сл едующему уравнению Эйлера

0 .

V dt

V V

В связи с тем, что

в функци ю

время

t явно не вхо-

дит, то первый интеграл уравнения Эйлера можно пол у- чить сразу в виде

P V P 0 . V

Подставив сюда производную	P	, получим:
Подставив сюда производную	V	, получим:

gCx V2S

g sin

gCx V2S

gCy V2S

g sin

g cos

gCx V2S

gCy V2S

g sin

g cos

Последнее, после несложных преобразований и введения

новых

обозначений:

a C

, в = C

, c = C

y 2G

1 G

Можно

записать в

более

простой

форме

g sin

2g a sin

в cos

2 2

g sin

g cos

вV

2 2

Постоянная C находится

из начальных

условий:

при t = 0, V = 0, V

V0 .

Разрешив

последнее

уравн ение относительно

V , получим

обыкновенное дифференциальное уравнение перв ого порядка. Его интегрирование в виду нелинейности целес о-

образно производить	численными методами на электро н-
но - вычислительных	машинах.

Зная зависимость V (t), легко определяются затем и о с-

тальные характеристики P (t),		(t), L (t), H (t).
4	.6. Определение посадочной дистанции самолета
В	общем случае процесс	посадки самолета состоит

из 5 этапов:

1	. Планирование		с безопасной высоты			полета. По
нормам ICAO для пассажирских самолетов					за	безопа сную
высоту при		посадке	принимается	высота	H бе з = 15 м.
2	. Выравнивания.
3	. Выдерживания.
4	. Парашютирования.
5	. Пробега по посадочной полосе.
Рассмотрим расчет этих этапов:
1	. На	участке	планирования	сила тяги		двигателей

обычно близка к нулю. Поэтому расчет этого участка

можно

вывести

по формулам

полученным

в параграфе

«Планирование

самолета

в однородной среде». А име нно

Lпл

KHбез ,

пл

K пл

Vпл

SCy пл

где Kпл = Cу пл / С х пл

качество самолета.

Обычно

Cу пл

= ( 0,6

0,7 ) Cу max .

2. Так как длина участка траектории выравнивания

небольшая, то

можно

принять,

что скорость

полета на

этом участке остается постоянной и равной скорости планирования Vпл , и траектория полета представляет с о- бой дугу окружности. В этом случае путь, пройде нный самолетом на участке выравнивания, равен

	S	плR	,
где R - радиус	кривизны	траектории.
Вследствие	малости	угла	нак лона траектории пл
можно принять,	что
	Lвыр	S	плR .

При выравнивании центростремительное ускорение с амолета, очевидно, равно:

V2	Y G cos
пл		.
R	m	.
R	m

Из последнего равенства в предположении cos = 1 следует, что

пл

g ny

Так как при планировании Y

G, то

Yвыр

Cy вырqвырS

Cy выр

Cy плqплS

Cy пл

В силу малости

угла

пл имеем, что

пл

K пл

Используя вышеприведенные равенства, получим, что

Lвыр

пл

qK пл Cy выр

Cy пл

3. На

участке

выдерживания

уравнения движения

самолета

имеют

вид:

Q ,

G = Y

Разделив

уравнения движения

одно на другое и и споль-

зуя замену переменных, получим, что

1 dV2

2g dL

K выд

Из последнего равенства следует, что

V 2

пл

Lвыд

K выдdV2 ,

2g V 2

min

где Vmin - минимальная скорость, при которой еще в ы- полняется условие Y = G.

Если учесть, что на участке выдерживания качес тво самолета меняется в узких пределах и, следовател ьно, в первом приближении может быть принято пост оянным, то получим, что

L			Kвыд	V	2	V	2	.
	выд
			2g	пл		min

4. Длина участка		парашютирования						самолета нев ели-

ка и при расчетах ее можно не принимать во вн имание. Однако сам процесс парашютирования весьма важен, так как он определяет важную характеристику с амолета - его посадочную скорость.

При расчетах	на этапе	парашютирования	будем п о-
лагать, что ускорение самолета по касательной			к трае к-
тории остается постоянным и равным своему			н ачально-
му значению, Cу =	Cу max и	вертикальная составляющая

скорости мала в сравнении с горизонтальной с оставляющей.

При принятых допущениях скорость полета сам олета по траектории на этапе парашютирования опред еляется уравнением:

= -

где правая часть есть константа.

Так как в начальный момент времени парашют иро-

вания

Y = G , то

Q =

После

преобразования

двух последних равенств

пр идем

к соотношению

интегрируя которое от

Vmin

до

V и от 0 до t,

получим,

что скорость на этапе парашютирования определ яется формулой

V = V	g	Cx	t .	(*)

min		Cy

Следовательно, подъемная сила на участке параш ю- тирования равна

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]