
Учебное пособие 1360
.pdfek+1,..., en - базис подпространства L2 .
Тогда объединение этих базисов образует базис во всем пространстве L , так как L = L1 L2 и dim L = dim L1 +dim L2 .
Найдем матрицу оператора A в этом базисе. В силу инвариантности подпространств L1 и L2 имеем:
|
|
|
Ae1,..., Aek L1 ; |
Aek+1,..., Aen L2 . |
|||||||||
Следовательно, верны равенства: |
|
|
|
|
|||||||||
|
Ae1 = a11e1 +... +ak1ek +0 ek+1 +... +0 en , |
|
|||||||||||
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
Aek = a1k e1 +... +akk ek +0 ek+1 +... +0 en , |
||||||||||||
|
Aek+1 = 0 e1 +... +0 ek +ak+1,k+1ek+1 +... +an,k+1en , |
||||||||||||
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
Aen = 0 e1 +... +0 ek +ak+1,nek+1 +... +annen . |
||||||||||||
Тогда |
матрица |
оператора A в базисе e1,..., en |
всего про- |
||||||||||
странства L имеет вид: |
|
|
|
|
|
|
|
|
|||||
|
|
|
a |
… |
a |
|
|
0 |
… |
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
11 |
|
1k |
|
|
|
|
|
|
|
|
|
|
|
… … … |
|
|
… |
… |
… |
|
|||
|
|
|
a |
… |
a |
|
|
0 |
… |
0 |
|
|
|
|
A |
= |
k1 |
|
kk |
|
|
|
|
|
|
, |
|
|
0 … 0 |
ak+1,k+1 |
|
|
|
||||||||
|
|
e |
|
… ak+1,n |
|||||||||
|
|
|
|
… … … |
|
|
… |
… |
… |
|
|||
|
|
|
|
0 |
… |
0 |
|
a |
|
… |
a |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
n,k+1 |
|
nn |
|
|
|
|
|
|
|
|
|
|
|
|||||
или |
A = |
A1 |
O , где A - матрица оператора A в под- |
||||||||||
|
e |
|
O |
A |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
пространстве L1 , A2 - матрица оператора A в подпространстве L2 . ■
Верно и обратное утверждение: если матрица оператора A в некотором базисе имеет клеточно-диагональный вид, то пространство L распадается в прямую сумму инвариантных относительно A подпространств L1 и L2 .
Определение. Матрица вида (13) называется полураспавшейся, а матрица вида (14) - распавшейся на клетки A1 и
A2 . Произвольная квадратная матрица называется приводи-
мой или разложимой, если она подобна соответственно полураспавшейся или распавшейся матрице.
Изучение многих свойств линейного оператора с полураспавшейся или распавшейся матрицей облегчается тем, что сводится к изучению пространств меньших размерностей.
Примером может служить следующее утверждение.
|
|
|
|
|
|
|
|
A |
B |
|
Теорема 25. Пусть U есть матрица вида |
или |
|||||||
|
|
|
|
|
|
|
|
O |
C |
A |
O |
. Тогда χU (λ) = χA (λ) χC (λ) , |
где χU (λ) , |
χA (λ) , |
|||||
|
|
||||||||
O |
C |
|
|
|
|
|
|
|
|
χC (λ) - |
характеристические многочлены матриц U , A , C |
||||||||
соответственно. |
|
|
|
|
|||||
|
Доказательство. Рассмотрим самую общую ситуацию, |
||||||||
|
|
A |
B |
характеристического |
|||||
когда U = |
. По определению |
||||||||
|
|
O |
C |
|
|
|
|
||
многочлена имеем |
|
|
|
|
|||||
|
|
χ |
(λ) =|U −λE |= |
|
A −λE |
B |
|
. |
|
|
|
|
|
|
|||||
|
|
U |
|
|
O |
C −λE |
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда в силу одного из свойств определителей (см. теорему Лапласа, п.2.6 части 1 настоящего пособия) получаем:
χU (λ) =| A −λE | | C −λE |= χA (λ) χC (λ) . ■
80 |
81 |
2.8.Аннулирующий и минимальный многочлены линейного оператора
Введем понятие многочлена от оператора.
Определение. k -ой степенью Ak |
линейного операто- |
|||
ра A называется оператор, определяемый равенством |
||||
|
Ak = A A ... A |
( k |
). |
|
|
k |
раз |
|
|
Нулевая степень A0 оператора A определяется равен- |
||||
ством: |
A0 = I , где I - единичный оператор. |
|||
Определение. Пусть L - линейное пространство над |
||||
полем |
P ; A : L → L |
- линейный |
оператор. Пусть |
|
f (x) = an xn +an−1xn−1 +... +a0 - многочлен с коэффициентами ai P . Оператор вида
f (A) = an An +an−1An−1 +... +a0I
называется многочленом от оператора A .
Дадим определение аннулирующего многочлена. Определение. Многочлен f (x) P[x] называется ан-
нулирующим многочленом оператора A , если f ( A) = O .
Заметим, что правая часть равенства f (A) = O - это ну-
левой оператор, т.е. такой, что Ox =θ x L .
У каждого линейного оператора есть ненулевой аннулирующий многочлен. Это, например, его характеристический многочлен χA (λ) =| A −λE | . Этот факт вытекает из
следующей теоремы.
Теорема 26 (Гамильтона-Кэли). Любой линейный опе-
ратор является корнем своего характеристического многочлена, т.е. χA ( A) = O .
Заметим, что для одного и того же оператора можно построить несколько аннулирующих многочленов. Действиительно, если f (x) - аннулирующий многочлен, то всякий
многочлен вида f (x)g(x) g(x) P[x] также будет аннулирующим, так как
f (A)g( A) = O g(A) = O .
Введем понятие минимального многочлена. Определение. Аннулирующий многочлен наименьшей
степени со старшим коэффициентом, равным единице, назы-
вается минимальным многочленом оператора.
Обозначение: mA (x) .
Теорема 27. Минимальный многочлен для любого оператора единственный.
Доказательство. Предположим, что m1(x) и m2 (x) -
два минимальных многочлена оператора A . Тогда разность m1(x) −m2 (x) является аннулирующим многочленом опера-
тора A , так как
m1( A) −m2 ( A) = O −O = O .
Причем по условию deg m1(x) =deg m2(x), а значит deg(m1(x) −m2(x)) <degm1(x) . Но это невозможно, так как m1(x) - аннулирующий многочлен наименьшей степени. Следовательно, m1(x) −m2 (x) = 0 (нулевой многочлен), от-
куда m1(x) = m2 (x) . ■
Теорема 28. Минимальный многочлен является делителем аннулирующего многочлена.
Доказательство. Пусть f (x) и m(x) - аннулирующий
и минимальный многочлены для оператора A . Разделим с остатком f (x) на m(x) :
82 |
83 |
f (x) = m(x)q(x) +r(x) , deg r(x) < deg m(x) .
Тогда
r(A) = f (A) −m(A)q(A) = O −O q(A) = O ,
значит r(x) - аннулирующий многочлен оператора A , причем его степень deg r(x) < deg m(x) . Но m(x) - аннулирую-
щий многочлен наименьшей степени. Следовательно, случай r(x) ≠ 0 невозможен.
Таким образом, r(x) = 0 , тогда f (x) = m(x)q(x) , и m(x) - делитель f (x) . ■
Укажем формулу для построения минимального многочлена.
Рассмотрим характеристический многочлен | A −λE | оператора A и его минимальный многочлен mA (x) . Эти два многочлена связаны следующим соотношением:
|
|
|
mA (λ) = |
(−1)n | A −λE | |
, |
|
|||
|
|
|
∆n−1 |
|
|||||
|
|
|
|
|
|
|
|
||
где ∆n−1 - |
наибольший |
общий |
делитель |
всех миноров |
|||||
( n −1)-го порядка матрицы A −λE . |
|
|
|
||||||
Из формулы вытекает, что корнями минимального |
|||||||||
многочлена mA (λ) |
|
являются все различные корни характе- |
|||||||
ристического многочлена | |
A −λE | , причем если |
||||||||
| A −λE |= (−1)n (λ −λ )m1 (λ −λ )m2 |
...(λ −λ )mk , |
||||||||
|
|
|
|
|
|
1 |
2 |
|
k |
то |
|
(λ) = (λ −λ )s1 (λ −λ )s2 ...(λ −λ )sk , |
|||||||
m |
A |
||||||||
|
|
1 |
2 |
|
|
k |
|||
где 1 ≤ si ≤ mi |
|
i = |
|
. |
|
|
|
|
|
|
1, k |
|
|
|
|
||||
Укажем одно из приложений минимальных многочле-
нов.
Теорема 29. Матрица A Mn×n (P) приводима (т.е.
подобна полураспавшейся матрице) тогда и только тогда, когда ее минимальный многочлен приводим над полем P .
Пример 41. Построим минимальный многочлен линейного оператора, имеющего матрицу
|
|
|
|
|
|
|
|
1 |
2 |
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
−2 −1 |
|
|
|
|
||||
1) |
|
Найдем |
сначала |
характеристический |
|
многочлен |
||||||||||
| A −λE | : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| A −λE |= |
|
1−λ |
2 |
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
|
2 −λ |
0 |
= −(λ −1)(λ −2)(λ +1) . |
||||||||||
|
|
|
|
−2 |
|
−2 |
−1−λ |
|
|
|
|
|
|
|
||
2) Найдем ∆2 - НОД всех миноров второго порядка |
||||||||||||||||
матрицы A −λE . Замечаем, что миноры |
|
|
|
|
||||||||||||
M1,3 = |
|
1−λ |
2 |
|
= 2(1+λ) |
и |
M 2,3 |
= |
|
0 |
2 −λ |
|
= 2(2 −λ) |
|||
|
|
|
|
|||||||||||||
1,2 |
|
−2 |
|
−2 |
|
|
|
|
|
1,2 |
|
|
−2 |
−2 |
|
|
взаимно простые, поэтому их наибольший общий делитель равен 1. Следовательно, ∆2 =1 и
ϕ(λ) = (−1)3 | A −λE | =| A −λE |= (λ −1)(λ −2)(λ +1) ,
∆2
т.е. минимальный многочлен ϕ(λ) совпадает с характеристическим многочленом с точностью до знака.
84 |
85 |
§ 3. ПРОСТРАНСТВА СО СКАЛЯРНЫМ ПРОИЗВЕДЕНИЕМ
При изучении векторов плоскости и пространства в аналитической геометрии важную роль играло понятие скалярного произведения векторов
(a,b) =| a | | b | cos(a,b) .
В произвольном линейном пространстве мы не можем таким образом определить скалярное произведение, поскольку у нас нет пока понятий длины вектора и угла между векторами. Попытаемся в общем случае определить скалярное произведение аксиоматически, взяв за основу известные свойства скалярного произведения векторов плоскости.
3.1.Евклидово пространство. Основные свойства, примеры
Пусть L - вещественное линейное пространство. Определение. Говорят, что в вещественном линейном
пространстве L задана операция скалярного произведения, если каждой паре векторов x, y L поставлено в соответст-
вие вещественное число (x, y) так, что выполнены следую-
щие аксиомы:
1) (x, y) = ( y, x) симметричность;
2) |
(x + y, z) = (x, z) +( y, z) |
аддитивность; |
|
3) |
(λx, y) = λ(x, y) , λ |
однородность; |
|
4) |
(x, x) ≥ 0 |
для любого x L , причем |
|
|
(x, x) = 0 |
тогда и только тогда, когда x =θ |
|
(положительная определенность).
Число (x, y) называется скалярным произведением векторов x и y , аксиомы 1 - 4 называются аксиомами ска-
лярного произведения.
Определение. Вещественное линейное пространство с заданным на нем скалярным произведением, называется евклидовым пространством.
В дальнейшем евклидово пространство будем обозначать E .
Замечание. Из аксиом 1 - 3 скалярного произведения вытекает аддитивность и однородность по второму аргументу. Действительно:
′ |
|
|
|
2 |
) (x, y + z) = ( y + z, x) = ( y, x) +(z, x) = (x, y) +(x, z) ; |
|
|
′ |
) (x, λy) = (λy, x) = λ( y, x) = λ(x, y) . |
|
|
3 |
|
|
|
Приведем примеры евклидовых пространств. |
|
n |
|
Пример 42. В арифметическом пространстве |
L = |
||
скалярное произведение векторов x = (x1, x2 ,..., xn ) |
и |
||
y = ( y1, y2 ,..., yn ) можно определить равенством |
|
|
|
|
n |
|
|
|
(x, y) = x1y1 + x2 y2 +... + xn yn = ∑xi yi . |
(15) |
|
i=1
Покажем это. Проверим аксиомы 1 - 4 скалярного произведения.
1) Докажем симметричность. Имеем:
( y, x) = y1x1 + y2 x2 +... + yn xn .
Так как xi , yi , то yi xi = xi yi , поэтому
( y, x) = x1 y1 + x2 y2 +... + xn yn = (x, y) .
86 |
87 |
2) Докажем аддитивность. Для вектора x + y = (x1 + y1, x2 + y2 ,..., xn + yn ) имеем:
(x + y, z) = (x1 + y1)z1 +(x2 + y2 )z2 +... +(xn + yn )zn =
=(x1z1 + y1z1) +(x2 z2 + y2 z2 ) +...+(xn zn + yn zn ) =
=(x1z1 + x2z2 +...+ xnzn ) +(y1z1 + y2z2 +...+ ynzn ) =(x, z) +(y, z) .
3) |
Докажем |
однородность. |
Для |
вектора |
λx = (λx1, λx2 ,...,λxn ) |
имеем: |
|
|
|
(λx, y) = (λx1) y1 +(λx2 ) y2 +... +(λxn ) yn =
=λ(x1 y1 + x2 y2 +... + xn yn ) = λ(x, y) .
4)Проверим свойство положительной определенности.
Имеем:
(x, x) = x2 |
+ x2 |
+... + x2 |
≥ 0 x L . |
1 |
2 |
n |
|
Кроме того, равенство x12 + x22 +... + xn2 = 0 выполняется тогда
и только |
тогда, когда |
x1 = x2 =... = xn = 0 , т.е. |
(x, x) = 0 x =θ .
Таким образом, все аксиомы скалярного произведения выполнены, а значит равенство (15) действительно задает
операцию скалярного произведения векторов x, y n .
В дальнейшем скалярное произведение, определенное формулой (15), будем называть каноническим.
Пример 43. В том же (см. пример 42) линейном про-
странстве L = n скалярное произведение можно определить по-другому.
Пусть α1,α2 ,...,αn - положительные действительные
числа. Тогда скалярное произведение можно задать формулой:
(x, y) =α1x1y1 +α2 x2 y2 +... +αn xn yn . |
(16) |
(Докажите!)
Пример 44. В пространстве L = n предложим еще одну формулу для скалярного произведения. Для векторов
x = (x1, x2 ,..., xn ) и y = ( y1, y2 ,..., yn ) положим |
|
(x, y) = (x1 − x2 )( y1 − y2 ) + x2 y2 +... + xn yn . |
(17) |
Докажите, что аксиомы 1 - 4 скалярного произведения будут выполнены.
Таким образом, линейное пространство L = n можно превратить в различные евклидовы пространства, определяя по-разному операцию скалярного произведения векторов, например, формулами (15), (16) или (17), или как-то иначе.
Пример 45. Пусть L = C[a,b] - пространство функций, непрерывных на отрезке [a,b] . Скалярное произведение век- торов-функций можно задать формулой
b |
|
( f , g) = ∫ f (t)g(t)dt . |
(18) |
a
Действительно, в силу свойств определенного интеграла имеем:
b b
1) ( f , g) = ∫ f (t)g(t)dt = ∫g(t) f (t)dt = (g, f ) .
a a
88 |
89 |

|
b |
2) ( f +h, g) = ∫( f (t) +h(t))g(t)dt = |
|
|
a |
b |
b |
= ∫ f (t)g(t)dt + ∫h(t)g(t)dt = ( f , g) +(h, g) . |
|
a |
a |
b |
b |
3) (λ f , g) = ∫λ f (t)g(t)dt = λ∫ f (t)g(t)dt = λ( f , g) .
a a
b
4) Свойство ( f , f ) = ∫ f 2 (t)dt ≥ 0 верно, так как инте-
a
грал от неотрицательной функции всегда неотрицателен. Кроме того,
b
( f , f ) = 0 ∫ f 2 (t)dt = 0 f = 0 ,
a
так как интеграл от непрерывной неотрицательной функции равен нулю тогда и только тогда, когда функция равна нулю.
Таким образом, все аксиомы скалярного произведения выполнены. Следовательно, формула (18) действительно задает операцию скалярного произведения.
Наличие скалярного произведения позволяет ввести в
любом евклидовом пространстве геометрическую терминологию - определить понятия длины вектора, ортогональных векторов, угла между векторами. Сделаем это в последующих пунктах.
3.2.Унитарное пространство. Основные свойства, примеры
Пусть L - комплексное линейное пространство. В пространстве L введем операцию скалярного произведения.
Определение. Комплексное число (x, y) называется
скалярным произведением векторов x, y L , если выполня-
ются следующие аксиомы:
1)(x, y) = ( y, x) ;
2)(x + y, z) = (x, z) +( y, z) ;
3) |
(λx, y) = λ(x, y) , λ ; |
4) |
(x, x) ≥ 0 , (x, x) = 0 x =θ . |
Определение. Комплексное линейное пространство с заданным на нем скалярным произведением называется унитарным пространством.
Далее унитарное пространство будем обозначать U . Замечание. Из определения скалярного произведения
вытекает следующее.
1) (x, x) - это всегда действительное число. Покажем
это. В силу аксиомы 1 верно (x, x) = (x, x) , т.е. комплексное число (x, x) совпадает со своим сопряженным, а это свойст-
во выполняется только для действительных чисел, значит
(x, x) .
2) Из свойств 1, 2 вытекает аддитивность по второму аргументу:
(x, y +z) =(y +z, x) =(y, x) +(z, x) =(y, x) +(z, x) =(x, y) +(x, z) .
3) Из свойств 1, 3 не следует однородность по второму аргументу. Действительно, для любого комплексного числа λ имеем:
90 |
91 |

(x, λy) = (λy, x) = λ( y, x) = λ ( y, x) = λ (x, y) ,
или (x, λy) = λ (x, y) , т.е. из второго аргумента скалярного
произведения выносится не λ , а λ . Поэтому скалярное произведение в унитарном пространстве свойством линейности по второму аргументу не обладает.
Пример 46. В комплексном линейном пространстве L , dim L = n, скалярное произведение векторов x =(x1, x2,..., xn ) ,
y = ( y1, y2 ,..., yn ) , где xi , yi , можно задать следующим образом:
(x, y) = x1 y1 + x2 y2 +... + xn yn . (Докажите!)
3.3.Геометрия евклидовых и унитарных пространств
С помощью скалярного произведения введем геометрическую терминологию в евклидовых и унитарных пространствах.
Определение. Длиной (или нормой) вектора x в евклидовом или унитарном пространстве называется число

 x
x
 = (x, x) .
= (x, x) .
Из аксиом скалярного произведения вытекают следующие факты.
1) Любой вектор евклидова или унитарного пространства имеет длину, при этом 
 x
x
 ≥ 0 для любого x E(U ) и
≥ 0 для любого x E(U ) и

 x
x
 = 0 x =θ .
= 0 x =θ .
2) При умножении вектора x на число λ , его длина умножается на | λ | , т.е. 
 λx
λx
 =| λ |
=| λ | 
 x
x
 . Действительно,
. Действительно,
|
|
|
|
|
|
|
|
|
|
λx |
|
|
|
|
|
|
|
|
|
|
(x, x) =| λ | |
|
x |
|
, |
|
|
|
|
|
|
|
|
|
|
|
= (λx, λx) = λλ |
|
|
||||||||||||||
где λ |
или λ ; причем в случае λ |
имеем |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= (α +iβ)(α −iβ) =α2 + β2 =| λ |2 . |
||||||||||||||||
|
|
|
|
λλ |
||||||||||||||||||||||
Вектор единичной длины называется нормированным. |
||||||||||||||||||||||||||
Равенство |
|
|
|
λx |
|
|
|
=| λ | |
|
|
|
x |
|
|
|
дает возможность нормировать лю- |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
бой ненулевой вектор x , для этого вектор x |
надо разделить |
|||||||||||||||||||||||||
на его длину.
Только для евклидовых пространств можно определить понятие угла между векторами.
Определение. В евклидовом пространстве углом меж-
ду ненулевыми векторами |
x и |
|
y называется угол ϕ , |
||||
0 ≤ϕ ≤π , для которого |
|
|
|
|
|
|
|
cosϕ = |
|
(x, y) |
. |
||||
|
x |
|
|
|
|
||
|
|
y |
|
||||
|
|
|
|
||||
Если среди векторов x , y есть хотя бы одни нулевой,
то угол между такими векторами считается неопределенным. Отметим, что в унитарном пространстве понятие угла между векторами не определено, так как скалярное произведение (x, y) - это комплексное число. Однако, и в евклидо-
вом, и в унитарном пространстве можно ввести обобщение понятия прямого угла.
Определение. Векторы x , y евклидова или унитарно-
го пространства называются ортогональными, если их скалярное произведение равно нулю, т.е. (x, y) = 0 .
Обозначение ортогональных векторов: x y .
Вевклидовом пространстве ортогональность векторов
xи y означает, что либо один из них нулевой, либо угол
между ними равен π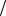 2 .
2 .
92 |
93 |

Контрольные вопросы и задания к п. 3.1-3.3
1.Сформулируйте определение евклидова пространства. Приведите пример такого пространства.
2.Каким образом можно ввести скалярное произведение в пространстве:
а) n ,
б) C[a,b] ?
3. Можно ли в вещественном линейном пространстве 2
ввести |
скалярное |
произведение |
по |
формуле |
(x, y) =| x1 | | y1 | +| x2 | | y2 |, где x = (x1, x2 ) , |
y = ( y1, y2 ) . |
|||
(Ответ: нет.)
4.Сформулируйте определение унитарного пространства. Приведите пример такого пространства.
5.Докажите следующие свойства скалярного произведения в унитарном пространстве:
а) (x, λy) = λ(x, y) ;
б) (x, y + z) = (x, y) +(x, z) .
6.Как определяются длина (норма) вектора и угол между двумя ненулевыми векторами в евклидовом пространстве?
7.Докажите, что в пространстве P2 многочленов степени, не превосходящей 2, скалярное произведение элементов f (x) и g(x) можно ввести по формуле
( f , g) = f (−1) g(−1) + f (0) g(0) + f (1) g(1) .
Вычислите нормы многочленов f (x) =1− x + x2 и g(x) =1+ x и угол между ними.
8.Можно ли в комплексном линейном пространстве квадратных матриц второго порядка ввести скалярное произведение по формуле:
а) ( A, B) = a1 a2 −b1 b2 +c1 c2 −d1 d2 , б) ( A, B) = a1 a2 +b1 b2 +c1 c2 +d1 d2 ,
|
a1 |
b1 |
|
|
a2 |
b2 |
|
|
|
где |
A = c |
d |
|
, |
B = c |
d |
2 |
|
. (Ответ: а) нет, б) да) |
|
1 |
1 |
|
|
2 |
|
|
|
|
9. Пусть u - фиксированный ненулевой вектор евклидова пространства, α - фиксированное число. Является ли множество всех векторов x , для которых (x,u) =α , подпространством данного евклидова пространства?
(Ответ: да, если α = 0 ; нет, если α ≠ 0 ) 10. Докажите, что:
а) если (x, y) = 0 для любого вектора x , то y =θ ;
б) если (x, y) = (x, z) для любого вектора x ( y и z - фиксированные векторы), то y = z .
94 |
95 |

3.4.Основные равенства и неравенства в пространствах со скалярным произведением
В пространствах со скалярным произведением справедливы неравенство Коши-Буняковского, неравенство треугольника и теорема Пифагора.
Теорема 29 (неравенство Коши-Буняковского). Для любых векторов x , y евклидова или унитарного простран-
ства справедливо неравенство
| (x, y) |≤ 
 x
x


 y
y
 .
.
Доказательство. Доказательство утверждения проведем отдельно для евклидова и унитарного пространств.
1)Пусть x , y - векторы евклидова пространства; пусть
α- произвольное действительное число. Рассмотрим вектор x −αy . В силу аксиомы 4 (положительная определенность)
скалярного произведения имеем:
(x −α y, x −α y) ≥ 0 α ,
откуда в силу аксиом 1 - 3 получаем:
(x −α y, x −α y) = (x, x −αy) −α( y, x −α y) =
=(x, x) −α(x, y) −α( y, x) +α2 ( y, y) =
=(x, x) −2α(x, y) +α2 ( y, y) ≥ 0 ,
или

 x
x
 2 −2α(x, y) +α2
2 −2α(x, y) +α2 
 y
y
 2 ≥ 0 α .
2 ≥ 0 α .
Влевой части получили квадратный трехчлен относительно
α, причем он должен быть неотрицателен при всех значениях α , а значит его дискриминант D должен быть ≤ 0 :
D = (2(x, y))2 −4 
 x
x
 2
2 
 y
y
 2 = 4((x, y)2 −
2 = 4((x, y)2 −
 x
x
 2
2 
 y
y
 2 ) ≤ 0 ,
2 ) ≤ 0 ,
откуда (x, y)2 ≤ 
 x
x
 2
2 
 y
y
 2 , или | (x, y) |≤
2 , или | (x, y) |≤ 
 x
x


 y
y
 , что и требова-
, что и требова-
лось доказать.
2) Пусть теперь x , y - векторы унитарного простран-
ства и α - произвольное комплексное число. Тогда в силу аксиомы 4 скалярного произведения верно
(x −αy, x −αy) ≥ 0 α .
Преобразуем скалярное произведение в левой части этого неравенства. В силу аксиом 1 - 3 скалярного произведения имеем:
(x −α y, x −α y) = (x, x −αy) +(−α y, x −α y) =
=(x, x) +(x, −α y) +(−α y, x) +(−α y, −α y) =
=(x, x) −α (x, y) −α ( y, x) +α α ( y, y) =
= 
 x
x
 2 −α (x, y) −α (x, y) +α α
2 −α (x, y) −α (x, y) +α α 
 y
y
 2 ≥ 0 α .
2 ≥ 0 α .
Положим α = |
(x, y) |
, здесь скалярное произведение (x, y) - |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 |
|
|
|
|
|
|
|
y |
|
|
|
2 - число действительное. Подста- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
комплексное число, а |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вим это значение α в последнее неравенство. Получим: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 − |
|
|
|
|
|
|
|
|
|
(x, y) |
− |
(x, y) |
|
|
|
|
+ (x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 ≥ 0 , |
||||||||||||||||||||||||||||||||
|
x |
|
|
|
(x, y) |
(x, y) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
(x, y) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
y |
|
|
|
2 |
|
|
|
|
|
|
y |
|
|
|
2 |
|
|
|
|
|
y |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − |
(x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
(x, y) |
≥ 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
96 |
97 |


 x
x
 2
2 
 y
y
 2 ≥ (x, y) (x, y) =| (x, y) |2 .
2 ≥ (x, y) (x, y) =| (x, y) |2 .
Откуда вытекает
| (x, y) |≤ 
 x
x


 y
y
 . ■
. ■
Неравенство Коши-Буняковского позволяет утверждать, что в евклидовом пространстве косинус угла между
векторами cosϕ = |
|
(x, y) |
по модулю всегда не превосходит |
|||||
|
x |
|
|
|
y |
|
||
|
|
|
|
|||||
|
|
|
|
|
|
|||
единицы.
Теорема 30 (неравенство треугольника). Для любых векторов x , y евклидова или унитарного пространства
справедливо неравенство

 x + y
x + y
 ≤
≤ 
 x
x
 +
+ 
 y
y
 .
.
Другими словами, в пространствах со скалярным произведением длина стороны треугольника не превосходит суммы длин двух других сторон.
Доказательство. 1) Проведем доказательство сначала для евклидова пространства. В силу аксиом скалярного произведения имеем:

 x + y
x + y
 2 = (x + y, x + y) = (x, x) +2(x, y) +( y, y) =
2 = (x + y, x + y) = (x, x) +2(x, y) +( y, y) =
=
 x
x
 2 +2(x, y) +
2 +2(x, y) + 
 y
y
 2 .
2 .
Всилу неравенства Коши-Буняковского для скалярного про-
изведения (x, y) верно (x, y) ≤| (x, y) |≤ 
 x
x


 y
y
 . Тогда
. Тогда

 x + y
x + y
 2 ≤
2 ≤ 
 x
x
 2 +2
2 +2 
 x
x


 y
y
 +
+ 
 y
y
 2 = (
2 = (
 x
x
 +
+ 
 y
y
 )2 ,
)2 ,
откуда

 x + y
x + y
 ≤
≤ 
 x
x
 +
+ 
 y
y
 .
.
2) Рассмотрим теперь унитарное пространство. Имеем:

 x + y
x + y
 2 = (x + y, x + y) = (x, x) +(x, y) +( y, x) +( y, y) .
2 = (x + y, x + y) = (x, x) +(x, y) +( y, x) +( y, y) .
Здесь скалярное произведение (x, y) - это комплексное чис-
ло. Пусть (x, y) = a +ib , тогда ( y, x) = (x, y) = a −ib , и верно соотношение
(x, y) +( y, x) = 2a ≤ 2 a2 +b2 = 2 | (x, y) |.
Следовательно,

 x + y
x + y
 2 ≤ (x, x) +2 | (x, y) | +( y, y) =
2 ≤ (x, x) +2 | (x, y) | +( y, y) = 
 x
x
 2 +2 | (x, y) | +
2 +2 | (x, y) | +
 y
y
 2 .
2 .
Отсюда, в силу неравенства Коши-Буняковского получаем

 x + y
x + y
 2 ≤
2 ≤ 
 x
x
 2 +2
2 +2 
 x
x


 y
y
 +
+ 
 y
y
 2 = (
2 = (
 x
x
 +
+ 
 y
y
 )2 ,
)2 ,
тогда

 x + y
x + y
 ≤
≤ 
 x
x
 +
+ 
 y
y
 . ■
. ■
Теорема 31 (Пифагора). Для любых ортогональных векторов x , y евклидова или унитарного пространства
верно

 x + y
x + y
 2 =
2 = 
 x
x
 2 +
2 + 
 y
y
 2 .
2 .
Доказательство. По условию |
x y , значит |
(x, y) = ( y, x) = 0 . Тогда |
|

 x + y
x + y
 2 = (x + y, x + y) = (x, x) +(x, y) +( y, x) +( y, y) = = (x, x) +( y, y) =
2 = (x + y, x + y) = (x, x) +(x, y) +( y, x) +( y, y) = = (x, x) +( y, y) = 
 x
x
 2 +
2 + 
 y
y
 2 . ■
2 . ■
98 |
99 |
