Методическое пособие 590

Если выборка (число изделий, подвергающихся испытанию) растет, то можно от статистических закономерностей перейти к вероятностным, так как при этом эмпирическая функция распределения приближается к теоретической функции распределения:

Fn (x) F(x),

среднеарифметическое (средневыборочное) приближается к математическому ожиданию:

x M(x) x f (x) dx,

0

а выборочная дисперсия – к дисперсии генеральной совокупности:

s2 2 (x) D(x) x M(x) 2 f (x) dx.

0

Пример расчета статистических характеристик вариационного ряда

Задание. Были проведены метрологические испытания прочности крепежных болтов с фиксацией времени момента их разрушения. Определить среднее значение наблюдений, среднеквадратичное отклонение наблюдений,

асимметрию и эксцесс. По полученным характеристикам построить эмпирическую функцию распределения, гистограмму плотности распределения и полигон относительных частот дискретного вариационного ряда. Исходные данные представлены в табл. 1.5 и 1.6.

Решение

Варианты xi и их частоты vi представлены в табл. 1.2.

21

формулы (1.1) и (1.2). Объем выборки определим из табл. 1.2 по формуле

k

n vi :

i 1

n 1 3 2 1 5 5 12 3 5 6 10 ... 2 1 100

r 1 3.3 lg(n) 1 3.3 lg(100) 7.6,

округляя значение количества интервалов до целого, примем r 8. Длина интервала будет

h 795 25 96.25. 8

Полученное значение длины интервала округлим до целого значения и получим

h100.

Втабл. 1.3 на основании проведенных расчетов заполнены первые четыре столбца.

Вычислим начальные и центральные эмпирические моменты. При

вычислении эмпирических моментов удобно переходить к относительным

значениям наработки

22

ui xi c , hi

здесь c – постоянная величина, за которую может приниматься значение xi,

соответствующее наибольшему значению mi , или значение xi, равноудаленное от краевых значений. Примем c 350, а hi h 100, тогда

ui xi 350. 100

Все вычисленные ui записаны в пятом столбец табл. 1.3.

Вычислим начальные и центральные моменты для относительных

Второй начальный момент будет

23

определяются из следующих соотношений:

2 a2 a12 2.56 0.6 2.2;

3 a3 3 a2 a1 2 a13 2.1 3 2.56 ( 0.6) 2 0.6 3 2.07;

4 a4 4 a3 a1 6 a2 a12 3 a14

14.68 4 ( 2.1) ( 0.6) 6 2.56 ( 0.6)2 3 ( 0.6)4 14.78.

Выполним обратный переход от относительных значений наблюдений к абсолютным и вычислим среднее значение и среднеквадратическое отклонение наработки:

x a1 h c 0.6 100 350 290;

s h 2 100 2.2 148.

Коэффициент асимметрии и эксцесс можно определить по условным эмпирическим моментам:

A x >0 и E x >0, следовательно, распределение имеет положительную асимметрию, и кривая распределения более островершинная, чем при нормальном распределении.

24

Подготовим табл. 1.4, в которую внесем данные, используя следующие формулы:

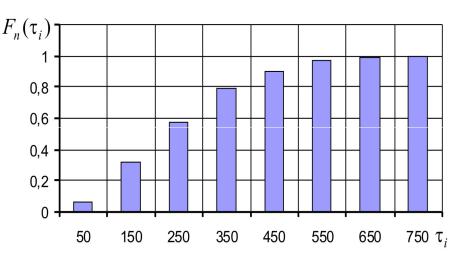
Построим эмпирическую функцию распределения Fn ( i ) и функцию плотности распределения f i , используя значения табл. 1.4. Для интервального вариационного ряда эмпирическая функция распределения имеет вид ступенчатой кривой, представленной на рис. 1.1.

Таблица 1.4

Данные для построения гистограмм и полигонов

Рис. 1.1. Эмпирическая функция распределения случайной величины

25

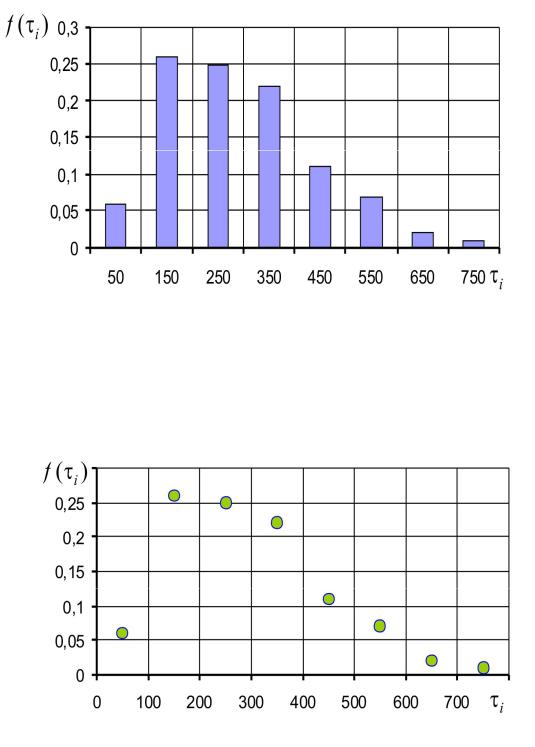
Рис. 1.2. Эмпирической функции плотности распределения случайной величины

Построим полигон относительных частот дискретного вариационного

ряда, используя данные табл. 1.4. Полигон показан на рис. 1.3.

Рис. 1.3. Полигон относительных частот дискретного интервального вариационного ряда

26

Таблица 1.5

Исходные данные значений варианты xi

Варианты задания

Таблица 1.6

Исходные данные значений частоты наблюдений vi

Варианты задания

27

Окончание табл. 1.6

Варианты задания

Оформление отчета

Отчет составляется по установленной форме и должен содержать

следующие пункты:

цель работы;

краткую теоретическую часть с расчётными формулами;

условие задания;

решение с пояснениями и формулами, написанными в буквенном и численном виде;

вывод.

28

Практическая работа № 2

ВЫБОР ФУНКЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ

ДЛЯ ПОЛИГОНА ОТНОСИТЕЛЬНЫХ ЧАСТОТ ДИСКРЕТНОГО

ИНТЕРВАЛЬНОГО ВАРИАЦИОННОГО РЯДА

Цель работы – изучить методику выбора и проверки правдоподобия аналитической функции плотности распределения случайной величины для полигона относительных частот дискретного интервального вариационного ряда. Приобрести навыки для использования критерия Пирсона при определении согласованности экспериментальных и теоретических значений.

Краткие теоретические положения

Выбор функции плотности распределения можно начать с анализа внешнего вида полигона относительных частот дискретного интервального вариационного ряда. Точки на графике (рис. 1.3) напоминают нормальный закон распределения случайной величины. Поэтому можно взять функцию вида

и, используя статистические данные, изобразить эту функцию на графике полигона относительных частот. Затем, используя критерий Пирсона, проверить правдоподобие выбранной функции плотности распределения.

Выполнены натурные испытания, которые позволяют построить статистический ряд

29