Методическое пособие 590

где a, b, v и C – постоянные величины.

Таким образом, каждое вторичное количество, удовлетворяющее условию абсолютного значения относительной величины, должно выражаться как некоторая постоянная, умноженная на первичные величины в некоторых степенях. Только вторичные величины такого рода применяются в научных измерениях, величины иного характера здесь не рассматриваются.

Классификация физических величин показана на рис. 2. Основным понятием для физических величин является основное уравнение измерения

(14)

где

Q – значение физической величины, которая показывает оценку её размера в идее некоторого числа принятых для нее единиц.

q – числовое значение физической величины, которое представляет собой число, выражающее отношение значения величины к соответствующей единице данной физической величины.

Q – единица физической величины фиксированного размера, которой условно по соглашению присвоено числовое значение, равное единице и применяемое для количественного выражения однородных физических величин.

10

Измерение – это процесс нахождения значения физической величины опытным путём с помощью технических средств.

Основная задача измерения – это поиск некоторой меры, которая позволяет проявиться исследуемой физической величине в виде числа при сравнении с некоторой мерой.

Результат измерения всегда определяется соотношением

Рис. 2. Классификация физических величин

В общем случае показатели размерности физических величин могут быть положительными, отрицательными, целыми либо дробными. Если в выражении

(13) a 0, b 0, v 0 и т.д., то физическая величина называется

безразмерной. Существуют три основных типа безразмерных физических величин:

относительные ФВ, выраженные в долях некоего условно принятого значения (например, относительная плотность – плотность вещества по отношению к плотности воды);

всевозможные коэффициенты, показывающие, во сколько раз одна величина больше другой в среде (например, коэффициент трения,

относительные магнитная и диэлектрическая проницаемости);

11

величины, характеризующие количество каких-либо объектов

(например, количество электронов в атоме).

Уравнение измерения является важным понятием в метрологии. Оно используется, например, для перевода показателей температуры из одной температурной шкалы в другую. Температурные шкалы относятся к общему понятию – шкалы интервалов.

Для шкалы интервалов уравнение измерения имеет вид

В качестве примера перевода значения из одной шкалы в другую рассмотрим температурные шкалы Цельсия, Фаренгейта, Реомюра. Эти шкалы характеризуются параметрами, которые представлены в табл. 2.

Пример. 1. Перевести значение температуры по шкале Фаренгейта в значение температуры по шкале Цельсия. Используем уравнение (17) и учтём,

что QC0 32 Q F , тогда запишем

Получим соотношение между шкалой Цельсия и шкалой Фаренгейта

5

tC 9 tF 32 .

2. Перевести значение температуры по шкале Реомюра в значение температуры по шкале Цельсия. Используем уравнение (17) и учтём, что

QC0 0 Q R , тогда запишем

12

Получим соотношение между шкалой Цельсия и шкалой Реомеюра

5 tC 4tR .

Погрешность измерений. При практическом использовании измерений всегда возникает вопрос о точности получаемых результатов. Точность измерений – это степень приближения результатов измерения к действительному или абсолютному значению, используется для качественного сравнения измерительных результатов. На рис. 3 показан качественных график соотношения точности измерений и погрешности измерений. Погрешность измерений – это количественная оценка точности измерения. Погрешность измерений важный показатель, который обеспечивает единство измерений.

Количество факторов, влияющих на точность измерений, велико.

Классификация погрешностей измерений показана на рис. 4. Для практических целей достаточно рассмотреть случайные и систематические погрешности,

которые могут выражаться в абсолютных и относительных единицах,

полученных при прямых, косвенных, совокупных и равноточных измерениях.

13

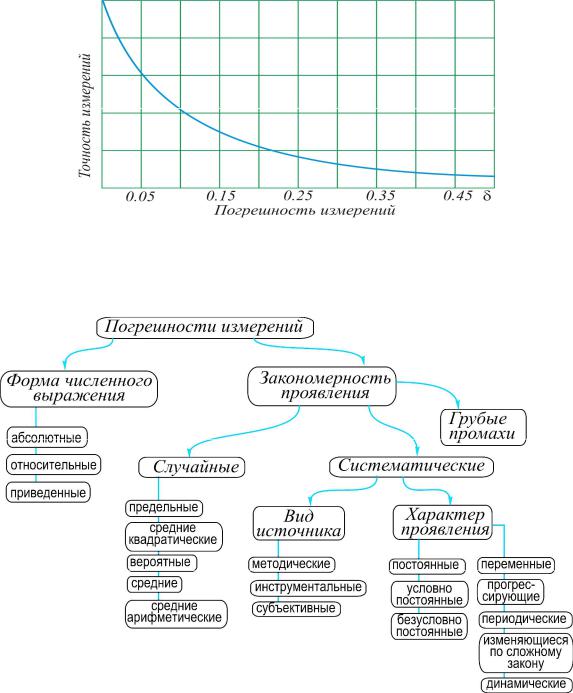
Рис. 3. График влияния погрешности измерений на точность результата измерений

Рис. 4. Классификация видов погрешностей

Относительная погрешность

14

Случайная погрешность – это составляющая погрешности измерений,

которая изменяется случайным образом в серии измерений физической величины. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерений. Описание случайных погрешностей возможно только на основе теории случайных процессов, теории вероятностей и математической статистики.

Случайные погрешности нельзя исключить из результатов измерений путем введения поправки, однако их можно уменьшить путем увеличения числа наблюдений. Поэтому для получения результата, минимально отличающегося от истинного значения измеряемой величины, проводят многократные измерения требуемой величины с последующей математической обработкой экспериментальных данных.

Систематическая погрешность – составляющая погрешности измерений, которая сохраняет постоянное значение или закономерно изменяет его при повторных измерениях одной и той же физической величины. Они могут быть предсказаны, обнаружены и почти полностью устранены введением соответствующей поправки.

Методическая составляющая погрешности измерений обусловлена несовершенством метода измерения, приемами использования средств измерения, некорректностью расчетных формул и округления результатов.

Инструментальная составляющая погрешности измерений возникает из-

за собственной погрешности средств измерения, которая определяется классом точности и разрешающей способностью средств измерения.

Субъективная составляющая погрешности измерений зависит от индивидуальных особенностей оператора (диагноста), его умения выполнять отсчет показаний по шкалам средств измерения, диаграммам регистрирующих приборов. Эта погрешность определяется состоянием диагноста, его положением во время работы, несовершенством органов чувств,

эргономическими свойствами средств измерений.

16

Практическая работа № 1

ОПРЕДЕЛЕНИЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ ДЛЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Цель работы – изучить методику обработки результатов метрологического контроля параметров различных объектов, приобрести навыки применения результатов статистического обследования действующего оборудования к решению прикладных вопросов метрологии.

Краткие теоретические положения

Результатом метрологического обследования всегда бывает ряд значений измеряемого параметра, который подчиняется определённому закону распределения. Для выявления этого закона проводят группировку полученных значений параметра по достаточно малым интервалам. Вычисление относительных частот проводят для каждого интервала значений, определяя числовые характеристики статистического распределения и получая графическое представление результатов в виде гистограмм, полигонов и эмпирических функций распределения. Выборочные наблюдения располагают в порядке возрастания в виде ряда

x1 x2 x3 xi xn 1 xn .

Полученный ряд называют вариационным, или ранжированным, а

различные значения xi – вариантами (i 1,2, ,n). Одна и та же варианта в ранжированном ряду может встретиться несколько раз. Число наблюдений с одинаковым значением варианты называют частотой и обозначают vk . Если значение x1 наблюдалось v1 раз, x2 наблюдалось v2 раз, x3 – v3 раз и т. д.

Образует ряд частот

v1,v2,v3, ,vk .

17

Если число членов вариационного ряда велико: n 100, то для удобства его изучения группируют наблюдавшиеся значения по интервалам, образуя интервальный ряд. Длину интервала можно брать одинаковой. Интервальный ряд может быть построен как для дискретных, так и для непрерывных случайных величин. Число интервалов r определяют, используя правило Старджесса для выборки объема n:

k

где n vi , т.е. сумма частот равна объему выборки.

i 1

Длина интервала

r

Отношение частоты к объему наблюдений называют относительной частотой

Варианты и соответствующие им частоты образуют статистический ряд наблюдений, который позволяет определять следующие статистические характеристики.

Выборочное среднее

n

xi

Выборочная дисперсия при n 20

18

где j – среднее значение j-го интервала.

Наиболее полно характеризует выборку, по сравнению с рассмотренными выше статистическими характеристиками, эмпирическая функция распределения, гистограмма и полигон. Графический вид функции может быть определен до момента его представления на основании табл. 1.1.

19