
Методическое пособие 582
.pdf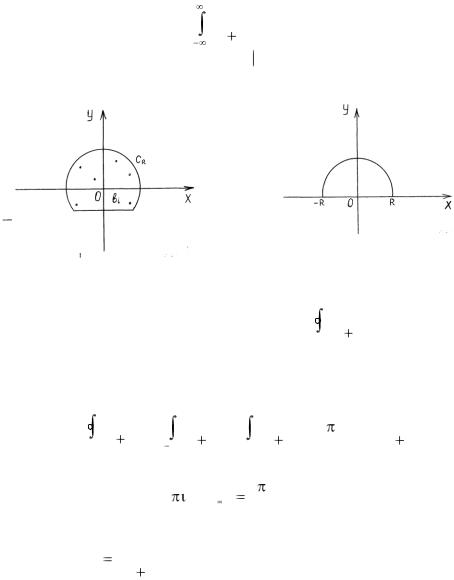
Лемма Жордана приводится здесь без доказательства. Лемма Жордана используется для вычисления некоторых несобственных интегралов.
Пример. Вычислить |
cos xdx |
. |
|
||
|
x2 a2 |
|
Пусть CR - дуга окружности z = R, расположенная в верхней полуплоскости Imz > 0 и пусть C – контур, состоящий из от-
= R, расположенная в верхней полуплоскости Imz > 0 и пусть C – контур, состоящий из от-
резка [-R, R] и дуги CR (рис. 1.30).
Рис. 1.29 Рис. 1.30
|
|
eiz dz |
||
Рассмотрим вспомогательный интеграл |
|
|
|
. |
C |
z 2 |
a 2 |
||
|
|
|
|
|
По основной теореме о вычетах
|
|
eiz dz |
|
R |
|
eix dx |
|
|
|
eiz dz |
|
|
eiz |
|||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
= 2 i Re s[ |
|
|
, ai] = |
||
|
C |
z 2 |
a 2 |
R |
x2 |
|
a2 |
C |
z2 |
a2 |
z2 |
a2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
= 2 |
|
|
en |
|
z ai |
|
|
|
|
|
. |
|
|
|
(1.100) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2z |
|
|
|
ae |
a |
|
|
|
|||||||||
|
f (z) |
eiz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Функция |
|
|
удовлетворяет условиям леммы Жордана. |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
z2 |
a2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
80

Поэтому
|
|
|
lim |
|
|
|
|
eiz dz |
|
|
= 0. |
|
|
|
||||||||||
|
|
|
C z |
2 |
|
|
|
a |
2 |
|
|
|
|
|||||||||||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из равенства (1.100) при R |
|
|
|
|
|
|
|
находим, что |
|
|
||||||||||||||
|
|
|
|
|
|
|
eix dx |
|
|
|
= |
|
|
|
|
|
, |
|
|
|
||||
|
|
|
|
|
x |
2 |
|
|
a |
2 |
|
|
|
|
a |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ae |
|
|
|
|
|||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos xdx |
+ i |
|
|
|
sin xdx |
= |
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
2 |
a |
2 |
|
|
|
|
x |
2 |
|
|
a |
2 |
|
ae |
a |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Приравнивая в этом равенстве действительную и мнимую части, получим
cos xdx |
= |
|
, |
sin xdx |
= 0. |
||||||
|
|
|
|
|
|
|
|
|
|||
x |
2 |
a |
2 |
a |
x |
2 |
a |
2 |
|||
|
|
|
ae |
|
|
|
|||||
В теории преобразования Лапласа лемма Жордана применяется в другой формулировке. Пусть CR - дуга окружности p = R, расположенная в полуплоскости Rep< a (Рис.1.31).
= R, расположенная в полуплоскости Rep< a (Рис.1.31).
Лемма. Если функция F(p) аналитична в полуплоскости Rep< a кроме конечного числа особых точек, ни одна из которых
не расположена на прямой Rep= a , и если lim F ( p) 0 , то при
p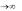
любом t > 0
lim e pt F( p)dp 0 .
R
CR
81
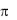
Вторая формулировка леммы получается из первой, если в ней сделать замену переменной iz = p. При такой замене плоскость комплексного переменного p получается из плоскости переменного z поворотом на угол /2 вокруг начала координат.
Рис.1.31
82

2.ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
2.1.Оригинал и изображение Лапласа
Комплексная функция f (t) = 1(t)+i 2(t) называется оригиналом, если для нее выполнены условия:
1. Функция f (t) непрерывна и имеет производные до неко-
торого порядка на всей числовой оси t (- <t< ) кроме отдельных точек, в которых функция или ее производные имеют разрывы первого рода, причем на каждом отрезке конечной длины таких точек конечное число.
2. f (t) = 0, если t < 0.
3.Функция f (t) при t + может расти не быстрее некоторой показательной функции. Это означает, что для каждой функ-
ции f (t) можно указать постоянные M и такие, что
f (t) |
e t. |
(2.1) |
Ясно, что если условие (2.1) выполняется для некоторого , |
||
то оно выполняется для любого > |
. Точная нижняя граница чи- |
|
сел , для которых выполняется неравенство (2.1), называется по-
рядком роста функции f (t) |
при t |
+ . Иными словами, число |
|
называется порядком роста функции |
|||
f (t) при t |
+ , если неравенство |
||
|
|
f (t) |
M e t |
выполняется при всех |
> |
и не выполняется при < . Напри- |
|
мер, если функция f (t) |
ограничена на всей числовой оси, то ее |
||
порядок роста равен 0. Нулевой порядок роста имеют также и степенные функции tn (n>0), так как для любой степенной функции tn
можно указать число M такое, что tn Me t при любом |
> 0, t > 0. |
||
Таким образом, условие 3 означает, что функция |
f (t) имеет |
||
конечный порядок роста при t + . Примером функции, |
|
|
|
для которой не выполняется условие 3, служит функция e |
t2 |
. |
|
|
|||
83
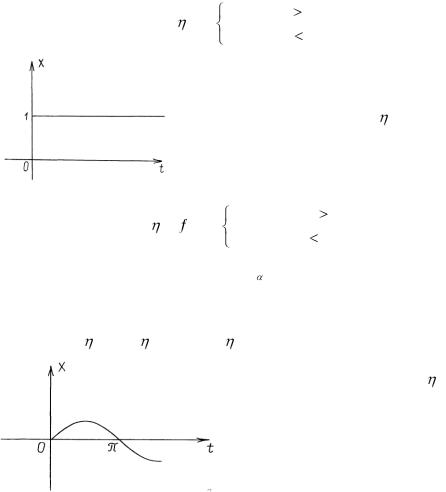
Простейшим примером оригинала является так называемая единичная функция Хевисайда (рис. 2.1).
(t)=
1, если t 0, 0, если t 0.
Если для функции f (t) выполнены условия1 и 3 и не выполняется условие 2, то для функции (t) f (t)
выполнены все три условия, предъявляемые к оригиналам, так как
Рис.2.1 |
|
|
|
|
(t) (t) = |
f (t), |
если t |
0, |
|
0, |
если t |
0. |
|
|
|
|
|||
Например, функции sint, cost, e t , tn и другие не |
являются |
|||
оригиналами, так как для них не выполнено условие |
f (t) = 0 |
|||
при t < 0. Поэтому в операционном исчислении рассматривают-
ся функции (t)sint, |
(t)cost, (t) (t)tn и другие, |
|
|
|
которые |
являются |
оригина- |
|
лами, при этом множитель (t) |
||
|
условились не писать, так что, |
||
|
например, |
функция |
f (t) = sint |
|
в операционном |
исчислении |
|
|
имеет график |
|
|
|
вида (2.2). |
|
|
Рис.2.2 |
|
|
|
Пусть функция |
f (t) является оригиналом. |
|
|
84

Преобразованием Лапласа или изображением функции |
f (t) |
|||||||||||||||
называется функция F( p) от комплексного переменного p = |
+i , |
|||||||||||||||
определяемая по формуле |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
F( p) = |
|
|
|
f (t) e pt dt . |
(2.2) |
||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Если функция F( p) является преобразованием Лапласа |
|||||||||||||||
|
функции f (t) , то этот факт записывается в виде: |
|
||||||||||||||
|
|
|
|
F( p) f (t) , f (t) |
|
F( p) , F( p) = L[ f (t) ]. |
|
|||||||||
Примеры: 1. Пусть f (t) =1 (то есть f (t) = (t)). Тогда |
|
|||||||||||||||
F( p) = |
e pt dt = (-1/p)e-pt |
|
|
|
= 1/p, если Rep > 0. |
|
||||||||||
|
0 |
|
|
|||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
. |
(2.3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
2. Пусть |
f (t) = eat , где |
a - |
постоянное комплексное или |
|||||||||||||
действительное число. Тогда |
|
|
|
|
|
|
|
|
||||||||
|
|
F( p) = |
eat e ptdt = |
e ( p a)t dt = |
|
|||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
= |
1 |
|
e ( p |
a)t |
|
|
|
1 |
|
|
, если Re p Re a , |
|
||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
p a |
|
0 |
|
p |
|
a |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
eat |
1 |
|
. |
|
|
|
|
|
(2.4) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p a |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теорема. Если оригинал (t) имеет порядок роста 0, то его изображение F(p) является аналитической функцией в полуплоскости Rep = > 0, причем F(p) 0, если Rep = 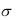 + . (рис. 2.3)
+ . (рис. 2.3)
По определению
85

F( p) = |
f (t) e pt dt . |
|
0 |
Покажем, что интеграл, стоящий в правой части этого равенства, сходится для всех
p = +i , если > 0.
|
Рис.2.3 |
|
|
|
|
|
|
|
|
В самом деле, пусть |
=Rep> 0. По условию теоремы |
|
f (t) |
||||||
|
|||||||||
Me t, для любого |
> 0, следовательно, |
|
|
|
|
||||
|
f (t) e-pt = f (t) e- t |
M e ( |
)t . |
|
|
||||
Так как |
- 0 > 0, то интеграл |
M e ( |
|
)t dt сходится, следова- |
|||||
|
|
|
0 |
|
|
|
|
|
|
тельно, интеграл |
f (t) e pt dt |
сходится абсолютно. Так как |
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
M e ( |
0 )t d t = |
0 при |
+ |
, |
|
|
||
|
0 |
|
|
|
|
|
|
|
|
то F( p) = |
f (t) e |
pt dt |
< M/( |
- 0) |
0 |
при |
+ . |
|
|
|
0 |
|
|
|
|
|
|
|
|
Аналитичность функции F( p) в полуплоскости Rep = > |
0 при- |
||||||||
мем без доказательства. |
|
|
|
|
|
|
|
||
2.2.Свойства преобразования Лапласа
2.2.1.Линейность преобразования Лапласа
86
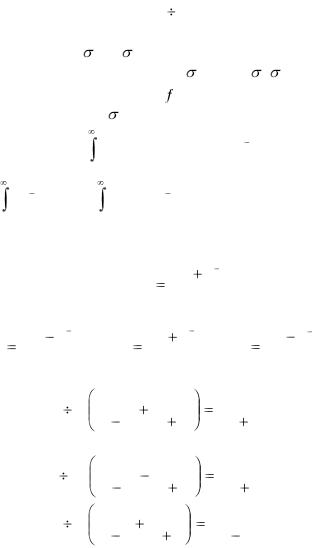
Теорема 1. |
Если функции |
f1 (t) |
и |
f2 (t) оригиналы, то |
|||||||||||||||||||||||||||||
функция f (t) = C1 f1 (t) +C2 f2 (t) , где C1 |
и C2 |
постоянные чис- |
|||||||||||||||||||||||||||||||
ла, также является оригиналом, причем |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
C1 f1 (t) |
+ C2 f2 (t) |
|
C1 |
F1 ( p) + C2 |
F ( p) . (2.5) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
В самом деле, пусть |
1 |
и |
2 |
|
- порядок роста соответственно |
||||||||||||||||||||||||||||
функций |
f1 (t) и f2 (t) . Тогда число |
= max{ |
1, |
2}, |
очевидно, |
||||||||||||||||||||||||||||
является порядком роста функции |
|
(t). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Поэтому, если Rep > |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
F( p) = |
|
[C1 f1 (t) +C2 f2 (t) ] e pt dt = |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= C1 |
|
e pt dt + C2 |
|
f2 (t) e pt dt |
= C1 F1 ( p) |
+ C2 F ( p) . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примеры. Найти изображения функций cosbt, sinbt, chbt, |
|||||||||||||||||||||||||||||||||
shbt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eibt |
|
e |
ibt |
|
|
|
|
|
|
||||
По формулам Эйлера cosbt |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin bt |
eibt |
e |
ibt |
|
ch bt |
|
ebt |
|
e bt |
|
|
|
|
ebt |
e bt |
||||||||||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
, |
sh bt |
|
|
|
|
|
. |
||||||||||
|
2i |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosbt |
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
p |
|
|
|
, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
p |
ib |
|
|
|
p |
|
ib |
|
|
|
p2 |
b2 |
|
|
|||||||||||||
|
|
sin bt |
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
b |
|
|
|
, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2i |
|
p |
ib |
|
|
|
p |
|
ib |
|
|
|
p2 |
b2 |
|
|
||||||||||||||
|
|
chbt |
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
p |
|
, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
p |
b |
|
|
p |
|
b |
|
p2 b2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
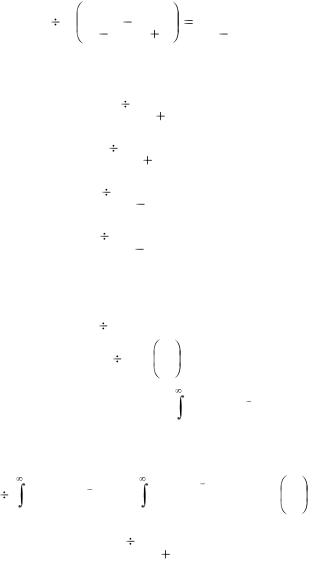
|
|
1 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
||
|
shbt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
2 |
|
p |
b |
|
|
|
|
p |
b |
|
|
p2 b2 |
|
|
|
|
|
||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosbt |
|
|
|
|
p |
, |
|
|
|
|
|
|
|
(2.6) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
p2 |
|
b2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
sinbt |
|
|
|
|
|
|
|
|
b |
|
|
, |
|
|
|
|
|
|
|
|
|
(2.7) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
p2 |
b2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
chbt |
|
|
|
|
|
|
|
p |
|
, |
|
|
|
|
|
|
|
|
|
|
|
(2.8) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
p2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
shbt |
|
|
|
|
|
|
b |
. |
|
|
|
|
|
|
|
|
|
|
(2.9) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
p2 |
b2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2.2.2. Теорема подобия |
|
|
|
|
|
||||||||||||||||||||||||
Теорема 2. Если |
f (t) |
F( p) , то для любого a >0, |
||||||||||||||||||||||||||||
|
|
|
f (at) |
|
|
|
|
1 |
F |
|
p |
. |
|
|
|
|
|
|
(2.10) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||
В самом деле, если в интеграле |
|
|
f (at) e pt dt |
сделать за- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
мену переменной a t=t1, dt=dt1/ a , то получим |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
1 |
|
|
p |
|
||
|
f (at) e pt dt = |
|
|
|
|
|
|
t1 dt = |
|
|
. |
|||||||||||||||||||
f (at) |
|
|
f (t )e |
|
a |
F |
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
a |
|
|
a |
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Например, зная, что cost |
|
|
|
|
p |
, находим |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
p2 |
1 |
|
|
|
|
|
||||||||||||||||||||
88

|
|
|
|
b |
|
|
1 |
|
|
|
||
cosbt |
b p |
2 |
p2 |
b2 , |
||||||||
|
|
|||||||||||
1 |
|
|
|
|
b |
|
|
|
p |
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
p
что совпадает с результатом (2.6).
2.2.3. Теорема о смещении изображения
Теорема 3. Если f (t) F( p) , то для любого постоянного комплексного числа a
|
|
f (t)eat F( p |
a) . |
|
|
|
(2.11) |
||||||
В самом деле, |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t)eat |
f (t)eat e pt dt = |
|
f (t)e ( p a )t dt = F( p a) . |
||||||||||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
С помощью теоремы 3 из соотношений (2.6)-(2.9) получаем |
|||||||||||||
|
eat cosbt |
|
|
|
p |
a |
|
|
, |
(2.12) |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
( p |
a)2 |
b2 |
||||||||
|
|
|
|
|
|
|
|||||||
|
eat sin bt |
|
|
|
b |
|
|
|
, |
|
(2.13) |
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
( p |
a)2 |
b2 |
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
|
eat |
ch bt |
|
|
p |
|
a |
|
|
, |
|
(2.14) |
|
|
|
|
|
|
|
|
|
|
|||||
|
( p a)2 |
b2 |
|
||||||||||
|
|
|
|
|
|
|
|||||||
|
eat |
sh bt |
|
|
|
|
b |
|
|
|
|
. |
(2.15) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
( p |
a)2 |
b2 |
||||||||
|
|
|
|
|
|
|
|||||||
2.2.4. Дифференцирование оригинала
Теорема 4. Если функции f (t) и f ' (t) – оригиналы и если f (t) F( p) , то
f ' (t) |
p F( p) - f (0) . |
(2.16) |
89
