Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 582

.pdf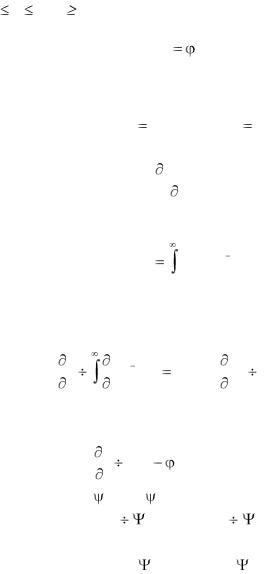

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

Разберем первую краевую задачу для уравнения (2.54): най-

ти решение и

(х,

t) дифференциального уравнения

(2.54)

для 0 x l и t

0, удовлетворяющее начальному условию

u(x,0)

(x)

(2.55)

и краевым условиям

u(0, t)

ψ1 (t),

u(l, t)

ψ2 (t),

(2.56)

Предположим, что u(x, t),

2u(x, t)

f (x, t) рассматривае-

мые как функции t, являются оригиналами. Обозначим через

U ( p, x)

u(x, t)e pt dt

(2.57)

– изображение функции и (х, t).

Тогда

e pt dt

d 2U

(2.58)

dx2

По правилу дифференцирования оригиналов получаем с

учетом начального условия (2.55):

(x) .

(2.59)

Предположим, что

1 (t) и

2 (t) являются оригиналами и

ψ1 (t)

1 ( p),

ψ2 (t)

2 ( p) .

(2.60)

Тогда граничные условия (2.56) дают

U|x=0=

1 (p), U|x=l=

2(p).

120

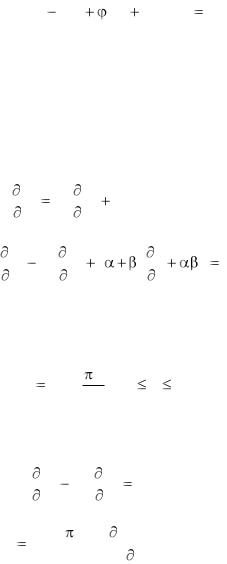
Таким образом, операторный метод приводит решение задачи (2.54), (2.55), (2.56) к решению обыкновенного дифференциального уравнения

a	2	d 2U	pU (x) F(x, p) 0	(2.62)
		dx2

при граничных условиях (2.61), где F (х, р) = f (х, t). Решая задачу (2.62), (2.61) и обращая полученное решение, найдем функцию и(х,t), являющуюся решением задачи (2.54), (2.55),

(2.56). Аналогично решаются и другие краевые задачи для уравнения теплопроводности, а также краевые задачи для уравнения колебаний струны

2u	a2	2u	f (x, t)	(2.63)
t 2		x2

телеграфного уравнения (см. [5 ])

2u	a2	2u	(	)	u	u 0	(2.64)
t2		x2			t

и некоторых других уравнений более общего вида.

Задача. Концы струны x=0 и х=1 закреплены жестко. Нaчальное отклонение задано равенством

u(x,0) Asin l (0 x l) .

Начальные скорости равны нулю. Найти отклонения

и (х,t) при I >0.

Решение. Дифференциальное уравнение

0 .

(2.65)

t 2

Начальные условия

u(x,0) Asin

u(x,0)

=0,

(2.66)

121

краевые условия

u(0, t)

u(l, t)

0 .

(2.67)

Переходя к изображениям, будем иметь

d 2U

sin

(2.68)

dx2

x 0

x l

(2.69)

Решая уравнение (2.68), получим

U (x, p) C e px a

C e px a

sin

Учитывая краевые условия (2.69), найдем

U (x, p)

sin

l 2

Оригиналом для U (х, р) является функция

u(x, t)

Acos

sin

которая будет решением поставленной задачи.

122

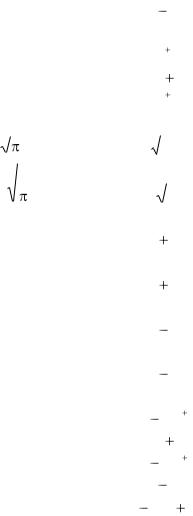
Таблица оригиналов и изображений

Номер формулы

Оригинал f(t)

Изображение F(p)

eat

tn (a > - 1)

Г (a 1)

cosbt

sinbt

chbt

shbt

tn eat

( p

a)n

ta eat

Г (a

( p

a)a

eat cosbt

( p a)2

123

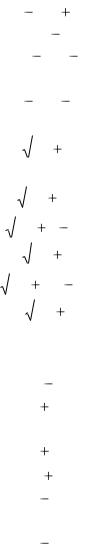
Продолжение

Номер форму-

Оригинал f(t)

Изображение F(p)

лы

eat sinbt

( p

a)2

eat chbt

( p

a)2

eat shbt

( p

a)2

J0(t)

J0(at)

Jn(t)

(

Jn(at)

(

sit

arctgp

tcosbt

( p2

b2 )2

tsinbt

2bp

( p2

b2 )2

tchbt

( p2

b2 )2

tshbt

2bp

( p2

b2 )2

124

ЗАКЛЮЧЕНИЕ Настоящее пособие написано авторами на основе многолет-

него опыта преподавания спецглав курса высшей математики в техническом университете и рассчитана на студентов тех специальностей, в программу которых входят разделы теории функций комплексного переменного и операционное исчисление. Материал пособия авторы постарались изложить так, чтобы максимально помочь читателю овладеть основами ТФКП и операционного исчисления. С этой целью в пособии разобрано большое количество примеров, которые помогут студентам глубже усвоить теоретический материал курса и приобрести навыки решения задач. Этот раздел служит теоретической базой в решении многих прикладных вопросов (ТОЭ), (ТАУ), (ТОК), и других общетехнических дисциплин.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Араманович И.Г., Лунц Г.А., Эльсгольц Л.Э. Функции комплексного переменного. Операционное исчисление. Теория устойчи-

вости. М.: Наука, 1965. 390 с.

2.Данко П.Е., Попов А.Г., Кожевникова Г.Я. Высшая математика в задачах и упражнениях. М.: Высш. шк., 1997. Ч.2. 415 с.

3.Диткин В.А., Прудников А.П. Операционное исчисление.

М.: Высш. шк., 1966. 408 с.

4.Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. М.: Наука, 1981. 302 с.

5.Левинштейн М.Л. Операционное исчисление и его приложения к задачам электротехники М.-Л.: Энергия, 1964. 466 с.

6.Мантуров О.В. Курс высшей математики. М.: Высш. шк., 1991. 448 с.

7.Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа. М.: Наука, 1980. 303 с.

125

8. Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. М.: Высш. шк., 1991. 448 с.

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1. ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО

ПЕРЕМЕННОГО . . . . . . . . . . . . . . . . . . . . . . . . . . .	. . . . . .
5
1.1. Комплексные числа и действия над ними . . . . .	. . . 5
1.1.1. Понятие комплексного числа. Алгебраическая,

тригонометрическая и показательная формы комплексного числа .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.1.2.Сложение и вычитание комплексных чисел . . 7

1.1.3.Умножение и деление комплексных чисел . . . 8

1.1.4.Возведение комплексных чисел в целую положительную

степень. Формула Муавра. Извлечение

корня из комплексных чисел . . . . . . . . . . . . . . . . . . .

1.2. Комплексная плоскость. Понятие области на комплексной плоскости. Понятие предела последовательности комплексных

чисел . . . . . . . . . . . . . . . . . . . . . . . . .	12
1.3. Комплексные функции . . . . . . . . . . .	. . . . . .	15
1.3.1. Комплексные функции действительного

126

переменного . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	15
1.3.2. Комплексные функции комплексного
переменного . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	16
1.4. Ряды с комплексными членами . . . . . . . . . . .	20
1.5. Элементарные функции комплексного
переменного. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	22

1.5.1. Показательная, тригонометрическая и гипер-болические функции комплексного переменного. Формулы Эйлера . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . 22

1.5.2. Логарифмическая функция комплексного переменного. Показательная функция с любым комплексным основа-

нием . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		26
1.6. Производная от функции комплексного перемен-
ного. Условия Коши – Римана . . . . . . . . . . . . . . .	. . . . . . .	27
1.7. Аналитические и гармонические функции.
Связь между ними . . . . . . . . . . . . . . . . . . . . . .	. .	34
1.8. Геометрический смысл модуля и аргумента
производной от функции комплексного переменного.
Понятие конформного отображения . . . . . . . . . .	. . . . .	38

1.9.Интеграл от функции комплексного переменного . 42

1.10.Теорема Коши для простого и сложного контура .46

1.11. Интегральная формула Коши . . . . . . . . . . . . .	.	50
1.12. Интегральная формула Коши для производных
от аналитической функции . . . . . . . . . . . . . . . . . . . . ..	. . . .	53
1.13. Степенные ряды в комплексной области . . . .	. .	55
1.14. Ряды Тейлора и Лорана . . . . . . . . . .. . . . . . . . .	.	57
1.15. Особые точки функции комплексного перемен-
ного. Классификация особых точек . . . . . . . . . . . . .	.	63
1.16. Вычет функции в особой точке. Основная

127

теорема о вычетах . . . . . . . . . . . . . . . . . . . . . .	. . . . .	66
1.17. Вычисление вычетов в простом и кратном
полюсе . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	. .	71
1.18. Некоторые применения вычетов . . . .	. . . . . . .	76
1.18.1. Вычисление интегралов
2
вида R(cost, sin t)dt . . . . . . . . . . . . . . . . . . . .	. . . . . .	76
0
1.18.2. Вычисление несобственных интегралов
с помощью вычетов . . . . . . . . . . . . . . . . . . . . .	. . . . . . . .	78
1.18.3. Лемма Жордана. Применение леммы к
вычислению несобственных интегралов . . . .	. . . . . . . . .	. 80
2. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ . . . . . . .	. . . . . . . . .	. 83
2.1 Оригинал и изображение Лапласа . . . . .	. . . . . .	83
2.2. Свойства преобразования Лапласа . . . .	. . . . . .	87
2.2.1. Линейность преобразования Лапласа . . . . .		87
2.2.2. Теорема подобия . . . . . . . . . . . . . . . .	. . . .	88
2.2.3. Теорема о смещении изображения .	. . . . . .	89
2.2.4. Дифференцирование оригинала . . .	. . . . . .	89
2.2.5. Интегрирование оригинала . . . . . . .	. . . . . . .	91
2.2.6. Дифференцирование изображения .	. . . . . . .	92
2.2.7. Интегрирование изображения . . . . .	. . . . . .	93
2.2.8. Теорема о запаздывании оригинала . . . . . .		.
Изображение периодических оригиналов . . .	. . . . . . . . .	. 94
2.2.9. Гамма - функция Эйлера. Изображение
степенных функций . . . . . . . . . . . . . . . . . . . . .	. . . . . . . . .	. 96
2.3. Обратное преобразование Лапласа . . .	. . . . . . . .	98
2.3.1. Применение вычетов для отыскания
обратного преобразования Лапласа . . . . . . . .	. . . . . . . .	. 100

128

2.3.2. Оригиналы рациональных изображений . .. .	102
2.4. Теорема об умножении изображений.
Интеграл Дюамеля . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	103
2.5. Теоремы о разложении . . . . . . . . . . . . . . . . . . .	106
2.6. Применения преобразования Лапласа . . . . . . . .	108
2.6.1. Решение задачи Коши для линейных
дифференциальных уравнений и систем с постоянными
коэффициентами. Применение интеграла Дюамеля . .	. . . 108
2.6.2. Решение интегральных уравнений . . . . . . . .	112
2.6.3. Решение задач электротехники . . . . . . . . .	114
2.6.4. Решение некоторых задач математической
физики. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	119
БИБЛИОГРАФИЧЕСКИЙ СПИСОК . . . . . . . . . . . . . . .	125

129

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20222.53 Mб8Методическое пособие 579.pdf
#
30.04.2022489.47 Кб8Методическое пособие 58.doc
#
30.04.2022326.25 Кб2Методическое пособие 58.pdf
#
30.04.20222.55 Mб6Методическое пособие 580.pdf
#
30.04.20222.55 Mб2Методическое пособие 581.pdf
#
30.04.20222.55 Mб3Методическое пособие 582.pdf
#
30.04.20222.56 Mб3Методическое пособие 583.pdf
#
30.04.20222.57 Mб5Методическое пособие 584.pdf
#
30.04.20222.59 Mб1Методическое пособие 585.pdf
#
30.04.20222.59 Mб3Методическое пособие 586.pdf
#
30.04.20222.6 Mб3Методическое пособие 587.pdf