
Методическое пособие 582
.pdf
X ( p) |
|
ab |
|
px0 |
x1 |
. |
( p2 |
a2 )2 |
|
p2 |
|
||
|
|
a2 |
||||
С помощью таблицы изображений и их оригиналов находим, что
x(t) |
b |
|
|
(sin at at cosat) |
x |
|
cosat |
|
x1 |
sin at . |
|||||
|
2 |
0 |
|
||||||||||||
|
2a |
|
|
|
|
|
|
a |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
При произвольных x0, x1 |
слагаемое x(t) |
x0 cos at |
|
x1 |
sin at |
||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
является общим решением однородного уравнения x" |
a2 x 0 , а |
||||||||||||||
слагаемое x* (t) |
|
|
b |
(sinat |
at cosat) |
|
является частным реше- |
||||||||
|
2a2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нием неоднородного уравнения x" |
a2 x |
bsinat . |
|
|
|||||||||||
Если начальные условия (2.39) нулевые, то в некоторых случаях решение уравнения (2.38) легче находить с помощью ин-
теграла Дюамеля.
Пусть требуется найти решение уравнения (2.38)
a |
0 |
x(n) |
a x(n 1) .... |
a |
n 1 |
x' |
a |
n |
x |
f (t) , |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
удовлетворяющее начальным условиям |
|
|
|
|
|
|||||||
|
|
x(0) x' (0) .... |
x( n |
1) (0) |
|
0 . |
(2.41) |
|||||
Для этого найдем решение вспомогательного уравнения |
|
|||||||||||
|
|
a |
x(n) |
a x(n 1) .... |
|
a |
x |
|
|
1 , |
|
(2.42) |
|
|
|
0 1 |
1 1 |
|
|
n 1 |
|
|
|
|
|
удовлетворяющее нулевым начальным условиям (2.41). Применяя преобразование Лапласа к уравнениям (2.38) и
(2.42), получим
1
A( p)X ( p) F( p) , A( p) X1 ( p) p .
Разделим почленно полученное первое уравнение на второе. Получим
X ( p) |
pF( p) , следовательно, |
X ( p) pX1 ( p)F( p) . |
||
|
|
|||
X |
1 ( p) |
|||
|
|
|||
Отсюда с помощью интеграла Дюамеля находим, что x(t) x'1 (t) * f (t) 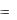 f (t) * x'1 (t) ,
f (t) * x'1 (t) ,
110

то есть
t |
|
t |
|
|
x(t) |
x'1 ( ) f (t |
)d = f ( )x'1 (t |
)d . |
(2.43) |
0 |
|
0 |
|
|
Применение интеграла Дюамеля оправдано в тех случаях, когда решается задача (2.38)-(2.41) для различных функций (t)
или тогда, когда трудно найти F(p). Пример. Найти решение задачи Коши
|
|
|
|
|
|
|
|
|
x" |
x |
|
e t2 , |
x(0) x' (0) 0 . |
|||||||
|
|
|
Для вспомогательной задачи |
|
|
|
|
|||||||||||||
x"1 |
x1 1, |
x1 (0) |
x'1 (0) 0 |
|
|
находим, |
что |
|||||||||||||
X |
|
( p)( p2 |
1) |
1 |
, |
X |
|
( p) |
|
|
|
1 |
|
, |
то есть |
|||||
1 |
|
|
p |
1 |
|
|
p( p2 |
1) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x1 (t) |
1 |
|
|
, x'1 |
(t) |
|
1 |
|
|
, |
следовательно, x'1 (t) sht . |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
p( p2 |
|
1) |
|
|
p2 |
1 |
|||||||||||||
Отсюда в силу (2.43) следует, что |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
x(t) |
e t2 |
|
* sht = |
e 2 sh(t |
)d . |
||||||||
0
Аналогично применяется преобразование Лапласа к решению систем линейных дифференциальных уравнений с постоянными коэффициентами. Например, пусть требуется найти реше-
ние задачи Коши для системы
x" |
x |
y |
z |
0 , |
x(0)=1, x(0)=0, |
x |
y" |
y |
z |
0 , y(0)=y(0)=0, |
|
x |
y |
z" |
z |
0, |
z(0)=z(0)=0. |
Применяя преобразование Лапласа к каждому уравнению системы, получим
p2 X ( p) |
p X ( p) Y ( p) Z ( p) 0 , |
X ( p) |
p2Y ( p) Y ( p) Z ( p) 0 , |
X ( p) Y ( p) p2 Z ( p) Z ( p) 0
111
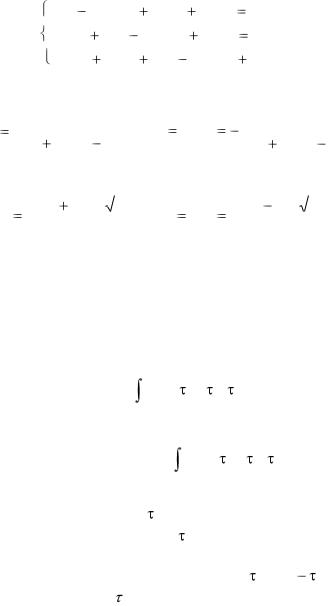
или
|
|
( p2 1) X ( p) Y ( p) Z ( p) p , |
|
|
|
|
|
|||||||||
|
|
X ( p) ( p2 |
1)Y ( p) Z ( p) 0 , |
|
|
|
|
|
||||||||
|
|
X ( p) Y ( p) ( p2 |
1)Z ( p) 0 . |
|
|
|
|
|
||||||||
Решая полученную систему алгебраических уравнений, |
||||||||||||||||
находим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
X ( p) |
|
p3 |
|
|
|
|
|
|
|
|
|
p |
||||
|
|
|
|
, Y ( p) |
Z( p) |
|
|
|
|
|
|
. |
||||
( p2 1)( p2 |
2) |
|
( p2 |
1)( p2 2) |
||||||||||||
Отсюда с помощью обратного преобразования Лапласа |
||||||||||||||||
находим, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x(t) |
|
cost 2 ch t |
2 |
, |
y(t) |
z(t) |
cost |
ch t 2 |
. |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
Преобразование Лапласа применяется также и для решения некоторых типов линейных дифференциальных уравнений с пе-
ременными коэффициентами.
2.6.2. Решение интегральных уравнений
Уравнения вида
t |
|
|
|
f (t) = |
k(t, |
)x( )d |
(2.44) |
0 |
|
|
|
и |
|
|
|
|
t |
|
|
x(t) = f (t) |
+ |
k(t, )x( )d |
(2.45) |
|
0 |
|
|
называются уравнениями Вольтерра соответственно первого |
|||
и второго рода. Здесь f (t) , k(t, |
) - заданные функции, |
x(t) - не- |
|
известная функция. Функция k(t, |
) называется ядром инте- |
||
грального оператора. |
|
||
Рассмотрим случаи, когда функция k(t, ) = k(t |
) зави- |
||
сит только от разности t- , то есть рассмотрим уравнения Вольтерра вида
112

t |
|
|
|
f (t) = k(t |
)x( |
)d |
(2.46) |
0 |
|
|
|
и |
|
|
|
t |
|
|
|
x(t) = f (t) + |
k(t |
)x( )d , |
(2.47) |
0
причем будем предполагать, что функции f (t) и k(t) являются
оригиналами. Применим преобразование Лапласа к правой и левой частям уравнений (2.46) и (2.47), при этом воспользуемся теоремой об умножении изображений. В результате получим
F( p) = K( p) X ( p) для уравнения (2.46)
и
X ( p) = F( p) + K( p) X ( p) для уравнения (2.47). Отсюда следует, что
F( p)
X ( p) K( p) или X ( p) 1 K( p) .
Неизвестная функция x(t) находится с помощью обрат-ного преобразования Лапласа.
Пример. Найти решение интегрального уравнения
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
x(t) |
= sint + |
|
(t |
|
)x( |
)d . |
||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Это уравнение Вольтерра второго рода. Так как |
|||||||||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t )x( )d |
|
= t * x(t) , то переходя к изображениям, |
|||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X ( p) |
|
1 |
|
|
|
|
X ( p) |
. |
|
|
|
|
|
|
|
p |
2 |
1 |
|
|
|
p2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Отсюда находим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
X ( p) |
|
|
p2 |
|
|
1 |
|
|
1 |
|
|
1 |
. |
||
|
( p2 |
1)( p2 |
1) |
2 |
|
|
p2 |
1 |
|
p2 1 |
|||||
113
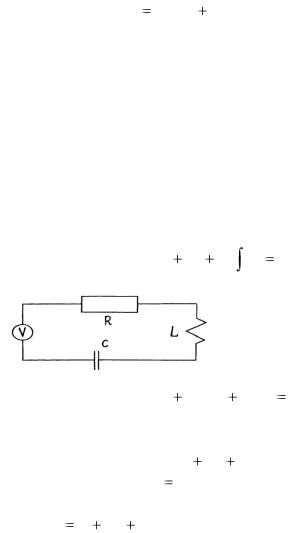
Следовательно, x(t) |
1 |
(sh t sin t) . |
|
2 |
|||
|
|
2.6.3. Решение задач электротехники
Применению преобразования Лапласа к решению задач электротехники посвящена большая специальная литература.
Подробную библиографию см., например /5/. Здесь мы рассмотрим лишь простейшие примеры.
Рассмотрим колебательный контур, в котором последовательно включены сопротивление R, индуктивность L и
емкость C (рис. 2.11). Уравнение, описывающее состояние колебательного контура, имеет вид
L |
di |
Ri |
1 t |
idt v(t) . |
(2.48) |
||
|
|
|
|||||
dt |
C 0 |
||||||
|
|
|
|
||||
Применяя преобразование Лапласа к уравнению (2.48) и предпола-гая, что i(0) = 0, полу-чим
Рис.2.11
|
LpI ( p) RI ( p) |
|
I ( p) |
V ( p) . |
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
Cp |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Отсюда находим, что |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
R Lp |
Cp |
= |
V ( p) |
, |
(2.49) |
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|||||||||
|
I ( p) |
|
|
|
|
|
Z ( p) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
V ( p) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Z ( p) R Lp |
|
1 |
|
называется операторным сопротивлени- |
|||||||||
|
Cp |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
ем цепи.
Формула (2.49) является операторной формой закона Ома. Из формулы (2.49) с помощью обратного преобразования
Лапласа можно найти силу тока
114
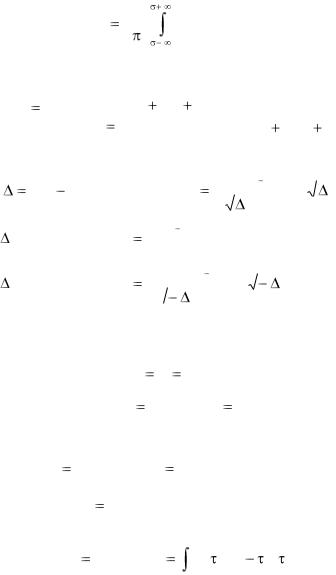
i(t) |
1 |
i |
V ( p) |
e |
pt |
dp . |
(2.50) |
2 i |
i |
Z ( p) |
|
||||
|
|
|
|
|
Например, пусть v(t)=E - в цепь включается постоянное напряжение. Тогда
V ( p) |
E |
, |
|
|
|
Lp2 |
Rp |
|
|
|
C |
=. |
E |
|
|
|
1 |
|
|
|
|
. |
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
p |
I ( p) |
|
|
L p2 |
|
|
|
R |
p |
1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CL |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
||||||||
Возможны следующие случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
Rt |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e 2 L sin t |
|
|
|
|
||||||||||||||||||
1) если |
|
|
|
|
|
|
> 0, |
то |
|
i(t) |
|
|
|
|
|
|
|
|
; |
|
|
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
CL |
|
4L |
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
Rt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2) если |
= 0, |
|
|
|
то |
i(t) |
|
te |
2 L ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
Rt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) если |
< 0, |
|
|
|
то |
i(t) |
|
|
|
|
|
e |
|
2 L sh t |
|
|
|
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
L
Впервом случае в цепи наблюдаются затухающие гармонические колебания, во втором и третьем случае – непериодический затухающий процесс. Пусть в контур включено постоянное
единичное напряжение v1(t) |
E |
1 . Тогда |
|
|
|
|||||||||
|
|
|
V ( p) |
1 |
|
, |
I |
( p) |
|
1 |
. |
|
||
|
|
1 |
|
|
p |
1 |
|
pZ( p) |
|
|||||
|
|
|
|
|
|
|
|
|
||||||
Если теперь в контур включить произвольное напряжение |
||||||||||||||
v(t) , то |
I ( p) |
|
V ( p) |
, |
I ( p) |
|
pV ( p) . |
|
|
|
||||
|
|
I1 ( p) |
|
|
|
|||||||||
|
|
|
Z ( p) |
|
|
|
|
|
|
|||||
Следовательно, |
I ( p) pI1 ( p)V ( p) . |
|
|
|
|
|
||||||||
Отсюда с помощью интеграла Дюамеля находим, что |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
i(t) i'1 (t) * v(t) |
i'1 ( )v(t |
)d |
(2.51) |
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
115

|
t |
|
|
i(t) v(t) * i'1 (t) |
v( )i'1 (t |
)d . |
(2.52) |
|
0 |
|
|
Формулы (2.51) и (2.52) показывают, что, не зная параметры контура, а зная лишь реакцию контура на единичное напряжение, можно рассчитать реакцию контура на любое напряжение v(t) .
Мы рассмотрели случай, когда i(0) = 0, v(0) = 0. Рассмотрим теперь случай, когда в начальный момент времени t=0 в контуре есть ток i0 и на обкладках конденсатора есть начальный заряд q0. Тогда состояние контура описывается дифференциальным урав-
нением
|
di |
|
1 t |
q |
|
|
|
||
L |
|
Ri |
|
idt |
0 |
v(t),i(0) i0 |
, |
(2.53) |
|
dt |
C |
C |
|||||||
|
|
0 |
|
|
|
||||
которое после применения преобразования Лапласа при-нимает вид
|
|
|
LpI ( p) |
Li0 |
RI ( p) |
|
I ( p) |
|
q |
V ( p) . |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Cp |
|
Cp |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Li0 |
|
q0 |
|
|
|
|
|
|
|
|
|
|
|
I ( p) |
|
V ( p) |
|
|
Cp |
|
, |
где Z ( p) Lp |
R |
1 |
. |
|||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
Z ( p) |
|
|
Z ( p) |
|
|
|
|
|
|
|
|
Cp |
|
||||
Таким |
|
|
образом, |
к |
току, |
|
|
определяемому |
изображением |
||||||||||||||
I1 ( p) |
V ( p) |
, добавляется ток, изображение которого имеет вид |
|||||||||||||||||||||
|
Z ( p) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Li0 |
|
q0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I2 ( p) |
|
|
|
Cp |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Z ( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
116

Этот ток называется током короткого замыкания. Он получается, если положить v(t) = 0, то есть накоротко замкнуть кон-
тур.
Рассмотрим теперь не один контур, а сложную электрическую цепь. Расчет электрических постоянного тока проводится
на основе законов Кирхгофа:
1. Алгебраическая сумма всех токов, притекающих к данной точке цепи, равна нулю.
2. Для каждого замкнутого контура алгебраическая сумма падений напряжения на отдельных ветвях цепи равна нулю.
В курсах электротехники доказывается, что если ток меняется во времени, то оба закона Кирхгофа остаются справедливыми также для операторных токов и операторных сопротивлений. Всякую электрическую цепь можно разбить на участки, содержащие один из трех возможных типов сопротивлений: активное сопротивление R, сопротивление индукции L и сопротивление емкости C. Зависимость напряжения от тока на отдельных участках цепи имеет вид
1) vR Ri , |
2) vL L |
di |
|
|
1 |
t |
|
|
, |
3) vC |
|
idt . |
|||
dt |
C |
||||||
|
|
|
|
0 |
Применяя преобразование Лапласа к этим равенствам, получим зависимость операторных напряжений от операторных токов.
1)V ( p) |
RI ( p) , 2) V ( p) |
pLI ( p) , 3) V ( p) |
I ( p) |
. |
|
||||
R |
L |
C |
Cp |
|
|
|
|
||
Эти соотношения объединяет операторная форма закона Ома
V ( p) Z( p)I ( p) ,
где Z( p) – операторное сопротивление цепи, зависящее от операторных сопротивлений
1
ZR ( p) R , ZL ( p) Lp , ZC ( p) Cp .
117
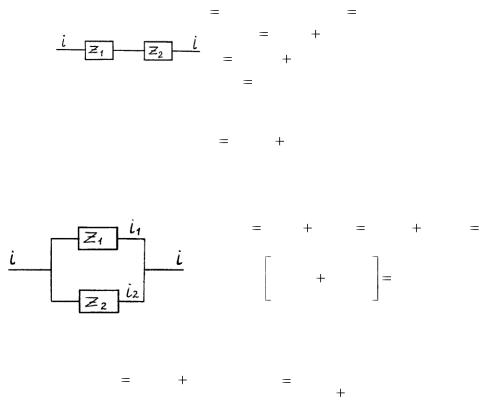
Рассмотрим возможные типы соединений отдельных сопротивлений в электрическую цепь. Сопротивления Z1 и Z2 соединены последовательно (Рис. 2.12). В этом случае
V1 ( p) Z1 ( p)I ( p) , V2 ( p) Z2 ( p)I ( p) , V ( p) V1 ( p) V2 ( p) 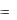
[Z1 ( p) Z2 ( p)]I ( p) 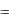
|
|
|
|
|
|
|
|
Z( p)I ( p) . |
|
|
|
|
|
|
|||||||
|
Рис.2.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, |
Z ( p) Z1 ( p) |
Z2 ( p) –при |
|
последова- |
|||||||||||||||||
тельном соединении операторные сопротивления складываются. |
|||||||||||||||||||||
2) сопротивления |
|
Z1 и |
Z2 |
соединены |
параллельно |
||||||||||||||||
(рис. 2.13). В этом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
I ( p) |
I1 |
( p) |
|
I2 ( p) |
|
V ( p) |
|
V ( p) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Z1 ( p) |
|
Z2 ( p) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
= V ( p) |
|
1 |
1 |
|
|
|
V ( p) |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Z1 ( p) Z2 ( p) |
|
|
Z ( p) |
|||||||||
|
|
|
|
|
|
Отсюда следует, что |
|
|
|
|
|
|
|||||||||
Рис. 2.13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
1 |
|
1 |
|
|
|
|
|
Z1 ( p)Z2 ( p) |
|
|
|
||||||||
|
|
|
|
|
|
|
, Z ( p) |
|
|
. |
|
|
|
||||||||
|
Z ( p) |
Z1 ( p) |
|
Z2 ( p) |
|
Z1 ( p) Z2 ( p) |
|
|
|
||||||||||||
Полученные соотношения для операторных сопротивле-ний и закон Ома в операторной форме позволяют составить операторное уравнение для любой электрической цепи.
Пример. Найти ток в контуре, изображенном на рис. 2.14, если i(0) = 0 и при t = 0 в цепь включается постоянное напряжение E.
Для параллельного участка цепи
118

|
1 |
|
Cp |
|
1 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 ( p) |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Z1 ( p) |
|
|
R |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
CRp |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.14 |
|||||
|
Для всей цепи Z( p) |
|
ZL ( p) |
Z1 ( p) |
|
|
Lp |
R |
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 CRp |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
= |
|
LCRp 2 |
Lp |
R |
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
CRP |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
По закону Ома I ( p) |
|
V ( p) |
, где V ( p) |
|
E |
. Следовательно, |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
Z ( p) |
|
|
p |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
I ( p) |
|
|
|
E(1 |
CRp) |
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
p(LCRp 2 Lp |
|
|
R |
|
|
||||||
Отсюда с помощью обратного преобразования Лапласа находится ток i(t).
2.6.4. Решение некоторых задач математической физики.
Ограничимся случаем, когда искомая функция и зависит от двух независимых переменных х и t. Переменную х будем рассматривать как пространственную координату, переменную t — как время.
Рассмотрим, например, уравнение теплопроводности
u |
a2 |
2u |
f (x, t) |
(2.54) |
|
t |
x2 |
||||
|
|
|
(а2 — постоянная).
119
