Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 582

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.55 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

1.4.Ряды с комплексными членами

Вкурсе математического анализа изучаются ряды, членами которых являются постоянные действительные числа или функции действительного переменного x. Точно так же можно рассматривать ряды с комплексными членами. Выражение вида

z1 + z2 + z3 + . . . + zn + . . .,

(1.13)

где z = x+iy – постоянные комплексные числа, называется числовым рядом с комплексными членами. Ряд (1.13) называется сходящимся,

если существует конечный предел lim sn	s ,	где sn = z1 + z2 +...+
n
zn– n-я частичная сумма ряда (1.13).
Наряду с рядом (1.13) рассмотрим ряды
x1 + x2 +...+ xn +...,		(1.14)
y1 + y2 +...+ yn +...,		(1.15)
z1 + z2 +...+ zn	+....	(1.16)

Справедливы следующие теоремы:

1)Ряд (1.13) сходится тогда и только тогда, когда сходятся ряды (1.14) и (1.15).

2)Если сходится ряд (1.16), составленный из модулей членов ряда (1.13), то ряд (1.13) также сходится. В этом случае говорят, что ряд (1.13) сходится абсолютно. Если же ряд (1.13) сходится, а ряд (1.16) расходится, то ряд (1.13) называется условно сходящимся.

Из этих теорем следует, что для определения характера сходимости рядов с комплексными членами можно применять теоремы о сходимости рядов с действительными членами.

Рассмотрим теперь степенной ряд в комплексной области

c0 + c1z + c2z2 +...+ cn zn +...,

(1.17)

где c0, c1, c2,..., cn,...– постоянные комплексные числа, а

z = x+iy – комплексная переменная. Для рядов (1.17), как и для степенных рядов в действительной области, справедлива теорема.

		Теорема Абеля. Если степенной ряд (1.17) сходится в точке
z0	0, то этот ряд сходится абсолютно в любой точке z, для кото-
рой		z < z0 . Если же ряд (1.17) расходится в точке z1, то этот
ряд расходится в любой точке z, для которой
z	>	z1 .
		Из теоремы Абеля также следует, что для степенного ряда
(1.17)		в комплексной области существует число R такое, что ряд
(1.17)		сходится в точках z, для которых z <R, и расходится в

точках, для которых z >R. Число R называется радиусом сходимости степенного ряда (4.5), а круг z <R - кругом сходимости этого ряда. В частности может оказаться, что R = , или R = 0. В первом случае степенной ряд сходится во всех точках комплексной плоскости, а во втором - в единственной точке z=0.

1.5. Элементарные функции комплексного переменного

1.5.1. Показательная, тригонометрические и гиперболические функции комплексного переменного. Формулы Эйлера

Рассмотрим степенной ряд

1 z	z2	...	zn	.... .
	2!		n!

Если z = x - действительное число, то этот ряд сходится на всей числовой оси и определяет функцию ex. . В силу теоремы Абеля, рассматриваемый ряд сходится на всей комплексной плоскости и определяет некоторую функцию комплексного переменного. Эта функция обозначается ez . Таким образом, по определению

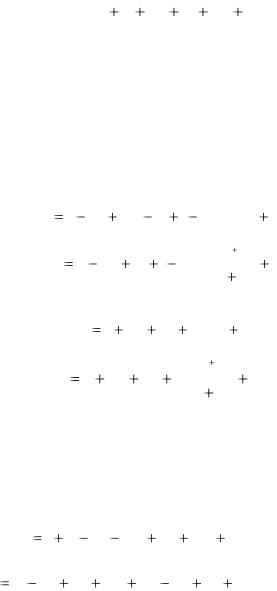
z		z2		zn
e = 1	z		...		.... .	(1.18)
e = 1	z	2!	...	n!	.... .	(1.18)
		2!		n!

Связь между функциями ez и ex такая же, как, например, между функциями z2 и x2: функция ez имеет более широкую область определения и совпадает с функцией ex при z=x. Говорят также, что функция ez является продолжением функции ex на комплексную плоскость, а функция ex - сужением функции ez на действительную ось.

Точно также определяются функции комплексного переменного cosz, sinz, сhz, shz как суммы соответствующих степенных рядов:

				z2			z 4								n z		2n
cos z	1									...		( 1)						... ,			(1.19)
cos z	1			2!						...		( 1)						... ,			(1.19)
				2!			4!									(2n)!
							4!									(2n)!
sin z		z			z3		... (					1)n			z 2n		1		....	,	(1.20)
sin z		z					... (					1)n							....	,	(1.20)
				3!										(2n			1)!
ch z 1								z	2		....		z 2n				.... ,				(1.21)

							2!						(2n)!
							2!						(2n)!
sh z			z			z3			....			z2n			1		.... .				(1.22)
sh z			z	3!					....			(2n			1)!		.... .				(1.22)
				3!								(2n			1)!

Из этих определений видно, что функции cosz и chz - четные, а sinz и shz - нечетные функции переменного z.

Если в равенстве (1.18) z заменить на iz, то, учитывая, что в абсолютно сходящемся ряде допустима любая группировка членов, получим

... =

....) i(z

....) ,

или

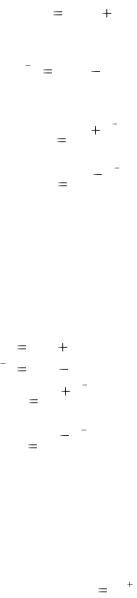
eiz cos z i sin z .

Если в этой формуле z заменить на -z, то получим, что e iz cos z i sin z .

Из равенств (1.23) и (1.24) находим, что

cos z	eiz	e	iz
				,
		2

	eiz	e	iz
sin z					.
		2i

(1.23)

(1.24)

(1.25)

(1.26)

Равенства (1.23) - (1.26) называются формулами Эйлера. Они устанавливают связь между тригонометрическими функциями и показательной функцией в комплексной области. Как известно, в действительной области эти функции не связаны между собой.

Точно так же устанавливается связь между гиперболическими функциями и показательной функцией:

ez	ch z		sh z ,				(1.27)
e z	ch z		sh z ,				(1.28)
ch z		ez	e	z
						,	(1.29)
			2			,	(1.29)
			2
sh z		ez	e	z
					.		(1.30)
			2		.		(1.30)
			2

Формулы (1.25), (1.26) и (1.29), (1.30) позволяют установить связь между тригонометрическими и гиперболическими функ-

циями:
chiz = cosz,	shiz = isinz,
	(1.31)
cosiz = chz,	siniz = ishz.
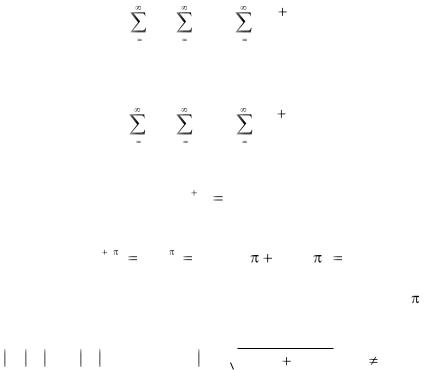
Рассмотрим равенство	ex1 ex2 ex1 x2 . С помощью рядов
это равенство означает, что

	xk	xk		( x	x	2	)k
	1	2	=	1		2
k 1 k! k 1 k!			=		k!
k 1 k! k 1 k!			k 1		k!

Так как перемножение рядов с комплексными членами проводится по тем же правилам, что и рядов с действительными членами, то

	z k			z k		(z	z	2	)k
	1	.		2	=	1		2		.
k 1 k!			k 1 k!		k 1		k!

Следовательно, формула

ez1 z2 ez1 ez2

(1.32)

справедлива для любых комплексных чисел z1 и z2. В частности,

ez 2 i ez e2 i ez (cos2

i sin 2 ) ez .

Отсюда следует, что функция ez периодична с периодом 2 i. Из формулы (1.32) следует также, что функция ez не обращается в 0 ни при каком комплексном z. В самом деле,

ez = ex+iy = ex(cosy+isiny) =ex 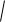cos2 y sin2 y = ex 0.

С помощью формул Эйлера также доказываются соотношения

cos(z1+z2) = cosz1 cosz2 - sinz1 sinz2,

sin(z1+z2) = sinz1 cosz2 + sinz2 cosz1,

ch(z1+z2) = chz1 chz2 + shz1 shz2,

sh(z1+z2) = shz1 chz2 + shz1 chz2.

С помощью этих формул получаем

cos2z = cos2z - sin2z , sin2z = 2sinz cosz,

ch2z = ch2z + sh2z , sh2z = 2shz chz,

cos2z + sin2z = 1, ch2z - sh2z = 1.

Основные соотношения для тригонометрических и гиперболических функций действительного переменного сохра-няются для соответствующих функций комплексного переменного. Однако неравенства

cosx 1, sinx 1

для функций cosz и sinz не сохраняются. Функции cosz и sinz могут принимать значения, сколь угодно большие по модулю. Например, при z = in имеем

cosin = (e-n + en)/2 > en/2.

1.5.2. Логарифмическая функция комплексного переменного. Показательная функция с любым комплексным основанием.

Комплексное число w называется логарифмом комплексного числа z, если ew = z. В этом случае пишут w = Lnz. Так как ew 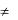0, то число z=0 не входит в область определения функции Lnz.

Если w = u+iv, z = r(cos +isin ), где r>0, то равенство ew = z принимает вид

eu+iv = r(cos +isin ), или eueiv = r(cos +isin ).

Отсюда следует, что

eu = r, eiv = cosv+isinv= cos +isin .

(1.33)

Из первого равенства находим, что u=lnr=ln z , где lnr означает логарифм натуральный для положительных чисел. Из второго

равенства (1.33) следует, что v = +2k	= Argz. Таким образом,
Lnz = ln z +iArgz = ln	z +iargz+2k i,	(1.34)

где k - любое целое число. Для любого числа z 0, Lnz принимает бесконечно много значений.

То значение Lnz, которое соответствует главному значению аргумента числа z, называется главным и обозначается через lnz. Следовательно,

		lnz = ln z	+iargz, Lnz = lnz+2k i.	(1.35)
Пример: Найти Ln(-1).
Так как	-1	= 1, arg(-1) = ,	то ln(-1) = ln1+ i =	i,
Ln(-1) =	i+2k	i = (2k+1) i.
Переходим к определению показательной функции с лю-
бым комплексным основанием c 0. Если c>0
и x – действительные числа,			то справедливо равенство

cx = exlnc.

Это равенство принимается за определение показательной функции от комплексного переменного z с любым комплексным основанием c 0. Таким образом, по определению, для любых комплексных чисел c 0 и z полагаем

cz = ezLnc.

(1.36)

Так как функция Lnz принимает бесконечно много значений, то и функция cz, определяемая равенством (1.36), многозначна. Его

главным значением считается то, которое получается, если в правой части равенства (1.36) вместо Lnс использовать lnс. Только при целых действительных z формула (1.36) определяет единственное значение cz.

Пример: Найти ii.

Так как i = 1, argi = /2, то Lni = 2k i+ i/2 = =(4k+1) i/2, то

ii = eiLni = e-(4k+1) /2,

где k - любое целое число. Главное значение ii равно e- /2.

1.6. Производная от функции комплексного переменного. Условия Коши - Римана

Пусть функция f (z) = u(x,y)+iv(x,y) определена в окрестности точки z = x+iy. Если переменной z придать приращение

z= x+i y, то функция f (z) получит приращение

f (z) = f (z+ z)– f (z) =u(x+ x, y+ y)+

+ iv(x+ x, y+ y) - u(x,y) - iv(x,y) = [u(x+ x, y+ y) –

– u(x,y)] + i [v(x+ x, y+ y) - v(x,y)] =

= u(x,y) + i v(x,y).

Определение. Если существует предел

lim	f (z)	= lim	f (z	z) f (z)	,
	z			z
z 0		z 0

то этот предел называется производной от функции f (z)										в точ-
ке z и обозначается через f (z) или					df (z)		. Таким образом, по оп-
ке z и обозначается через f (z) или							. Таким образом, по оп-
					dz
ределению,
	df (z)	= lim	f (z)	= lim		f (z		z) f (z)	.	(1.37)
	dz	z 0	z		z 0			z
		z 0			z 0

Если функция f (z) имеет производную в точке z, то говорят, что функция f (z) дифференцируема в точке z. Очевидно, для дифференцируемости функции f (z) необходимо, чтобы функции u(x,y) и v(x,y) были дифференцируемы. Однако этого не достаточно для существования производной f (z). Например, для функции w= z =x–iy функции u(x,y)=x

и v(x,y)=–y дифференцируемы во всех точках M(x,y), но предел

отношения	w	x	i y	при x	0,	y	0 не существует, так
	z	x	y

как, если	y = 0,	x		0, то	w/		z = 1,
если же x = 0,		y	0,	то	w/	z = -1.

Единого предела не существует. Это означает, что функция

w= z не имеет производную ни в одной точке z. Для существования производной от функции комплексного переменного требуются дополнительные условия. Какие именно? Ответ на этот вопрос дает следующая теорема.

Теорема. Пусть функции u(x,y) и v(x,y) дифферен-цируемы в точке M(x,y). Тогда для того, чтобы функция

f (z) = u(x,y) + iv(x,y)

имела производную в точке z = x+iy, необходимо и достаточно, чтобы выполнялись равенства

u(x, y)	v(x, y)	,	u(x, y)	v(x, y)	.	(1.38)
		,			.	(1.38)
x	y		y	x

Равенства (1.38) называются условиями Коши-Римана.

Доказательство. 1) Необходимость. Пусть

функция f (z)

имеет производную в точке z, то есть существует предел

f ' (z) = lim

f (z)

lim

u(x, y) i v(x, y)

.(1.39)

x i

0, y

Предел, стоящий в правой части равенства (1.39) не зависит

от того, по какому пути точка

z =

x+i

y стремится

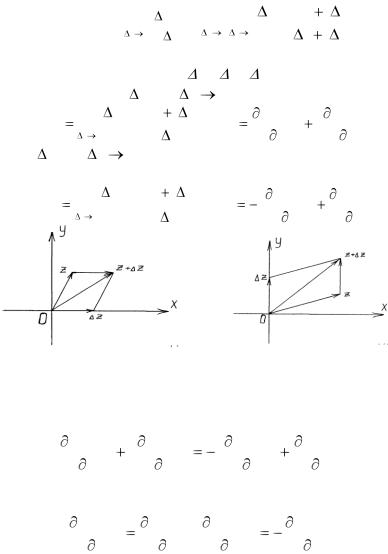
к 0. В частности, если

y = 0,

0 (рис. 1.10), то

f '(z)

lim

x u(x, y) i

x v(x, y)

u(x, y)

v(x, y)

(1.40)

Если же x = 0,

y 0

(рис. 1.11), то

f ' (z)

lim

y u(x, y)

y v(x, y)

u(x, y)

v(x, y)

(1.41)

Рис.1.10 Рис. 1.11

Левые части в равенствах (1.40) и (1.41) равны. Значит равны и правые части

u(x, y)

v(x, y)

u(x, y)

v(x, y)

Отсюда следует, что

u(x, y)

v(x, y)

u(x, y)

v(x, y)

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20222.53 Mб8Методическое пособие 579.pdf
#
30.04.2022489.47 Кб8Методическое пособие 58.doc
#
30.04.2022326.25 Кб2Методическое пособие 58.pdf
#
30.04.20222.55 Mб6Методическое пособие 580.pdf
#
30.04.20222.55 Mб2Методическое пособие 581.pdf
#
30.04.20222.55 Mб3Методическое пособие 582.pdf
#
30.04.20222.56 Mб3Методическое пособие 583.pdf
#
30.04.20222.57 Mб5Методическое пособие 584.pdf
#
30.04.20222.59 Mб1Методическое пособие 585.pdf
#
30.04.20222.59 Mб3Методическое пособие 586.pdf
#
30.04.20222.6 Mб3Методическое пособие 587.pdf