
Методическое пособие 582
.pdf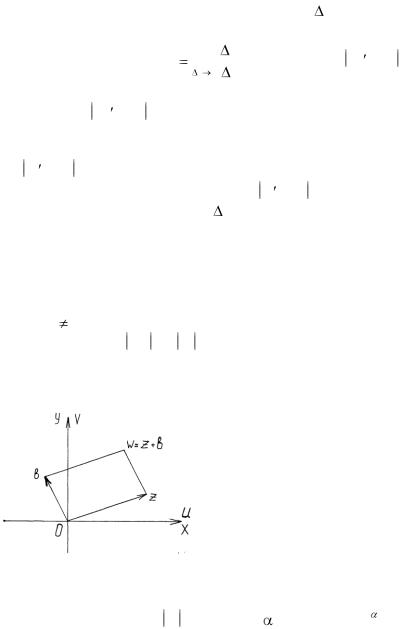
между |
точками |
|
z0 |
и |
|
z0 + |
z |
при |
отображении |
|||
w = f(z). |
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
|
f ' (z0 ) |
|
lim |
|
w |
|
, то величину |
f (z0) |
естественно |
||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
|
x |
||||||||||
|
|
|
|
|
z 0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
назвать коэффициентом растяжения в точке z0 |
при отображении w = |
|||||||||||
f(z). Если |
f |
(z0) > 1, то в достаточно малой окрестности точки z0 |
||||||||||
расстояние между точками при отображении увеличивается и проис-
ходит |
растяжение |
области, |
если |
же |
f (z0) |
< 1, то отображение w = |
f (z) в окрестности точки z0 при- |
||
водит к сжатию. Так как величина |
f (z0) |
не зависит от того, по ка- |
||
кому направлению точка z0+ z стремится к точке z0, то коэффициент растяжения в данной точке одинаков во всех направлениях.
В качестве примера рассмотрим отображение, осу-
ществляемое линейной функцией |
|
w = kz + b, |
1.50) |
где k 0, b - постоянные комплексные числа.
Так как w = k >0, то отображение (1.50) конформно во всех точках комплексной плоскости. Рассмотрим все возможные случаи, при этом для большей наглядности будем считать плоскость w совмещенной с плоскостью z.
= k >0, то отображение (1.50) конформно во всех точках комплексной плоскости. Рассмотрим все возможные случаи, при этом для большей наглядности будем считать плоскость w совмещенной с плоскостью z.
1. Пусть k = 1, то есть w = z + b. Так как сложение комплексных чисел равносильно сложению соответствующих векторов, то при отображении w = z + b точка w получается из точки z сдвигом на один и тот же вектор, соответствующий комплексному числу b
(рис. 1.14).
Рис. 1.14
В этом случае линейная функция (1.50) осуществляет параллельный перенос плоскости z на один и тот же вектор.
2. Пусть b = 0, k = 1, argk = , то есть w = ei z.
40
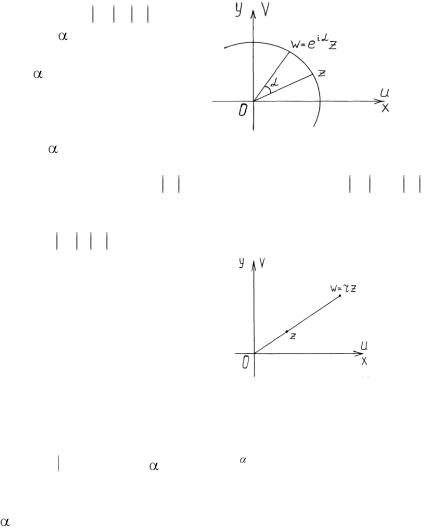
Так как при умножении комплексных чисел их модули
перемножаются, а аргументы |
|
складываются, то w = z |
, |
argw = argz+ . Поэтому вектор |
|
w получается поворотом вектора |
|
z на угол (рис. 1.15). Следова- |
|
тельно, в этом случае плоскость |
|
w получается из плоскости z по- |
|
воро |
|
том на угол . |
Рис. 1.15 |
3. Пусть b = 0, k = r > 0: w = rz. |
|
В этом случае argk=0, |
k =r, поэтому argw=argz, w = r z . |
Первое из этих равенств показывает, что точки w и z находятся на одном и том же луче, выходящем из начала координат, а из второго следует, что w / z = r = const (рис. 1.16).
Следовательно, в этом случае функция w = rz осуществляет преобразование подобия (гомотетию) с центром подобия в начале координат. Если же k = -r<0, то функция w= -rz, кроме преобразования по-
добия |
|
осуществляет еще и зеркальное |
|
отражение точки z от начала координат. |
Рис.1.16 |
4.Общий случай линейного преобразования w= kz+b сводится
крассмотренным выше простейшим преобразованиям. Действи-
тельно, если k = r, argk = , то w = rei z + b и переход от точки z к точке w осуществляется путем последовательного применения следующих операций: 1) поворота вектора z около начала координат на угол ; 2) преобразования подобия с центром подобия в начале координат и коэффициентом подобия r; 3) параллельного переноса на вектор, соответствующий комплексному числу b.
= r, argk = , то w = rei z + b и переход от точки z к точке w осуществляется путем последовательного применения следующих операций: 1) поворота вектора z около начала координат на угол ; 2) преобразования подобия с центром подобия в начале координат и коэффициентом подобия r; 3) параллельного переноса на вектор, соответствующий комплексному числу b.
41
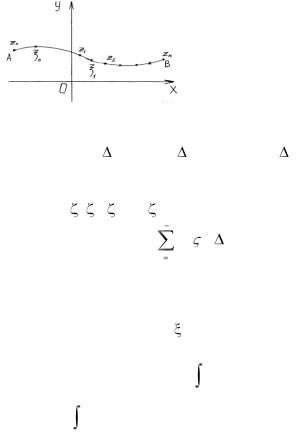
1.9. Интеграл от функции комплексного переменного
Пусть в плоскости комплексного переменного z дана замкнутая или незамкнутая кривая L, которую будем предполагать гладкой или кусочно-гладкой (это значит, что во всех точках кривой, кроме конечного числа, можно провести касательную).
Пусть A- начальная точка, а B –конечная точка кривой L. Тем самым на кривой L устанавливается положительное направление обхода, которое отметим стрелкой (Рис.1.17).
Предположим, что в точках кривой L задана непрерывная функция f (z) .
Разобьем кривую L на n частей точками
z0 = A, z1, z2, ..., zn = B, и
Рис.1.17 |
обозначим |
z1-z0 = z0, z2-z1 = |
z1 ,..., zn-zn-1 = zn-1. |
Внутри или на одном из концов каждой элементарной дуги вы-
берем по точке , 1, 2, ... , |
n-1 и составим сумму |
|
|
n 1 |
|
In= |
f ( k ) zk . |
(1.51) |
|
k 0 |
|
Определение. Если существует предел интегральной суммы (1.51), когда длина наибольшей из элементарных дуг стремится к 0, и если этот предел не зависит ни от способа разбиения кривой L на части, ни от выбора точек к в каждой
части, то этот предел называется интегралом от функции f (z) по
кривой L и обозначается через |
f (z)dz в случае незамкнутой |
AB
кривой, и через  f (z)dz в случае замкнутой кривой.
f (z)dz в случае замкнутой кривой.
C
42
Таким образом, по определению
|
|
|
n 1 |
|
|
f (z)dz = |
lim |
|
f ( |
k ) zk . |
(1.52) |
max |
zk |
0 |
k 0 |
|
|
AB |
|
|
|
|
Для интеграла от функции комплексного переменного справедливы следующие свойства:
1) |
[f1(z)+f2(z)]dz = |
f1(z)dz + |
f2(z)dz, |
|
AB |
|
|
AB |
AB |
2) |
kf(z)dz = k |
f(z)dz, |
|
|
AB |
|
AB |
|
|
где k - действительная или комплексная постоянная.
3) |
f(z)dz = - |
f(z)dz: |
BA |
|
AB |
если в интеграле направление интегрирования изменить на противоположное, то интеграл изменит знак,
4) |
f(z)dz = |
f(z)dz + |
f(z)dz, |
|
|
AB |
AC |
CB |
|
где C - внутренняя точка кривой AB. |
|
|||
5) Если во всех точках кривой L f(z) |
M, то |
|||
|
f(z)dz |
M l, |
|
|
|
AB |
|
|
|
где l длина кривой L.
Доказательство этих свойств проводится так же, как доказательство соответствующих свойств для определенных или криволинейных интегралов. Докажем, например, свойство 5).
Пусть f (z)  M. Тогда
M. Тогда
n |
1 |
n 1 |
|
|
|
|
|
f ( k ) zk |
|
f( k) |
zk |
|
|
k |
0 |
k |
0 |
|
|
|
|
n 1 |
|
|
|
|
|
|
M |
f ( |
k ) zk |
zk |
Ml, |
(1.53) |
|
k |
0 |
|
|
|
|
43

|
n 1 |
|
так как |
zk равна длине ломаной линии, вписанной в кри- |
|
|
k 0 |
|
вую L, а длина ломаной не больше длины кривой. |
||
Переходя к пределу при max zk |
0, получим |
|
|
|
|
f (z)dz |
M l. |
|
|
|
|
|
|
AB |
|
|
|
|
Установим теперь связь между интегралом от функции ком- |
|||||||
плексного переменного и криволинейными интегралами. |
|||||||
Пусть f (z) |
= u(x,y)+iv(x,y), |
zk = xk+iyk, |
|
|
|||
|
|
k = k+i k, zk = xk+i yk. |
|
|
|||
Тогда интегральная сумма (1.51) запишется в виде |
|
||||||
n 1 |
|
n 1 |
|
|
|
|
|
f( k) |
zk = |
[u( k, k)+iv[ k, |
k)]( |
xk+i |
yk] = |
||
k 0 |
|
k |
0 |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
= |
|
[u( k, k) xk-v( k, k)] xk + |
|
||||
|
k |
0 |
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
+ i |
[v( k, k) xk+u( k, k)] yk. |
|
|||||
|
|
k 0 |
|
|
|
|
|
Переходя в этом равенстве к пределу при |
x |
0, |
y 0 получаем, |
||||
что |
|
|
|
|
|
|
|
f (z)dz = |
|
u(x, y)dx v(x, y)dy + i v(x, y)dx |
u(x, y)dy . (1.54) |
||||
AB |
AB |
|
|
AB |
|
|
|
Вычисление интеграла от функции комплексного |
|||||||
|
|
|
переменного |
|
|
|
|
Пусть кривая |
L = AB имеет параметрическое уравнение |
||||||
x = x(t), y = y(t), причем точке A отвечает значение параметра t=t0,
44

а точке B - значение параметра t=T. Будем предполагать, что функции x(t) и y(t) непрерывно дифференцируемы на отрезке [t0,T]. Комплексно параметрическое уравнение кривой L имеет вид z = z(t), где z(t) = x(t)+iy(t).
Тогда, используя формулу для вычисления криволинейных интегралов и равенство (1.54), получим
f (z)dz = |
u(x,y)dx-v(x,y)dy+i v(x,y)dx+u(x,y)dy= |
|
AB |
AB |
AB |
= |
{u[x(t),y(t)]x (t) - v[x(t),y(t)]y (t)}dt + |
|
|
AB |
|
T
+ i {v[x(t),y(t)]x (t) + u[x(t),y(t)]y
(t) + u[x(t),y(t)]y (t)}dt =
(t)}dt =
t0
T
={[u(x(t),y(t)]+iv[x(t),y(t)]}[x (t)+iy
(t)+iy (t)]dt
(t)]dt
t0
или
|
|
T |
|
f (z)dz = |
f [z(t)]z' (t)dt . |
(1.55) |
|
AB |
|
t0 |
|
Пример. Вычислить |
(z-z0)ndz, где C - окружность |
с цен- |
|
C
тром в точке z0 радиуса R.
Комплексно параметрическое уравнение окружности C имеет вид z = z0+Reit . Поэтому
|
2 |
|
2 |
|
(z-z0)ndz = |
(Reit)niReitdt = Rn+1i |
eit(n+1)dt. |
C |
0 |
|
0 |
|
2 |
|
2 |
|
(z-z0)ndz = |
(Reit)niReitdt = Rn+1i |
eit(n+1)dt. |
C |
0 |
|
0 |
45
|
2 |
|
2 |
|
(z-z0)ndz = |
(Reit)niReitdt = Rn+1i |
eit(n+1)dt. |
C |
0 |
|
0 |
Если n=-1, то
|
dz |
2 |
|
|
= i |
||
|
|
||
C z z0 |
|||
0 |
|||
если же n -1, то
 (z-z0)ndz = Rn+1ei(n+1)t/(n+1)
(z-z0)ndz = Rn+1ei(n+1)t/(n+1)
C
dt = 2 i,
2 = Rn+1(ei2 (n+1)-1)=0.
= Rn+1(ei2 (n+1)-1)=0.
0
Таким образом
(z z )n dz |
2 i, |
если |
n |
1, . |
|
|
0 |
0, |
если |
n |
1 |
|
|
|
|
|
|
C |
|
|
|
|
|
1.10. Теорема Коши для простого и сложного контура
Простым контуром называется |
замкнутая кривая, не |
||
|
имеющая |
точек |
самопересечения |
|
(рис. 1.18). |
|
|
|
Теорема 1.Если функция f (z) ана- |
||
|
литична в замкнутой области D, ог- |
||
|
раниченной простым контуром С, |
||
|
то |
|
|
Рис. 1.18 |
f (z)dz 0 . |
(1.56) |
|
C
Доказательство. Пусть функция f (z) =u(x,y)+iv(x,y) анали-
тична в области D. Тогда во всех точках этой области выполняются условия Коши – Римана
u(x, y) |
|
v(x, y) |
, |
u(x, y) |
|
v(x, y) |
. |
|
|
|
|
|
|||
x |
|
y |
|
y |
|
x |
|
В силу (1.54)
46

f (z)dz = u(x, y)dx v(x, y)dy + i v(x, y)dx u(x, y)dy .
AB AB AB
Как известно, если во всех точках односвязной области выполняется условие
|
P(x, y) |
|
Q(x, y) |
, |
то |
P(x, y)dx Q(x, y)dy 0 . |
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
y |
|
|
|
x |
|
|
|
|
|
|
|
C |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
|
u(x, y) |
|
v(x, y) |
, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x |
|
|
|
y |
|
|
||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
v(x, y)dx u(x, y)dy 0 , |
|||||
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
||
а так как |
|
u(x, y) |
|
|
|
v(x, y) |
|
, то |
u(x, y)dx v(x, y)dy 0 , |
||||||
|
|
y |
|
|
|
y |
|||||||||
|
|
|
|
|
|
|
|
C |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следовательно,  f (z)dz 0 .
f (z)dz 0 .
C
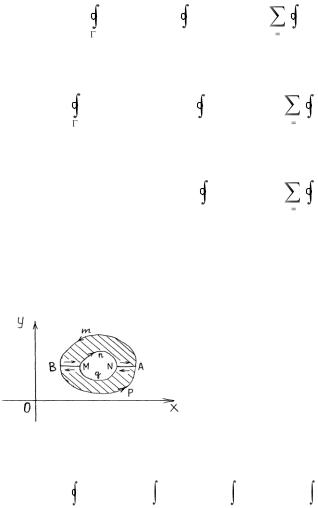
Пусть теперь D – многосвязная область, ограниченная внешним контуром C0 и внутренни-
ми контурами C1,C2,..., Cn (рис. 1.19). Граница области многосвязной области D называется сложным контуром и обозначается символом Г. Как было условлено ранее, положительным обходом контура Г называется такое движение по границе области, при котором
точки области остаются слева. Рис.1.19 Следовательно, положительное направление обхода внешнего контура против часовой стрелки, а внутренних контуров - по часовой стрелке.
47
Интегралом от функции f (z) по сложному контуру Г назы-
вается сумма интегралов от этой функции по всем граничным контурам, причем интегрирование по всем контурам проводится в одном и том же (положительном или отрицательном) направлении:
|
|
|
n |
|
|
|
f (z)dz = |
|
|
f (z)dz + |
|
|
f (z)dz . |
C |
0 |
|
k |
1 C |
k |
|
|
|
|
|
|
||
Теорема 2. Если функция f (z) аналитична в замкнутой об- |
||||||
ласти D, ограниченной сложным контуром Г, то |
||||||
|
|
|
|
n |
|
|
f (z)dz =0, или |
|
f (z)dz + |
|
|
f (z)dz = 0. (1.57) |
|
|
C |
0 |
|
k 1 C |
k |
|
|
|
|
|
|
||
Если направление интегрирования по внутренним контурам изменить на противоположное, то равенство (1.57) примет вид
|
|
n |
|
|
|
f (z)dz = |
|
f (z)dz , |
(1.58) |
C |
0 |
k 1 C |
k |
|
где интегрирование по всем контурам проводится по часовой стрелке.
Доказательство. Простоты ради рассмотрим случай, когда область D ограничена внешним контуром C0 и одним внутренним контуром C1 (рис.1.20). Разобьем область D на две
односвязные области D1 и D2 так, как это показано на рис. 1.20. Че-
|
рез |
L1=AmBMnNA |
|
и L2 |
= BpANqMB обозначим |
|
простые контуры, ограничиваю- |
|
|
щие соответственно облас- |
|
Рис.1.20 |
ти D1 |
и D2. |
По теореме Коши для простого контура имеем
f (z)dz = f (z)dz + f (z)dz + f (z)dz +
L1 AmB BM MnN
+  f (z)dz = 0,
f (z)dz = 0,
NA
48
f (z)dz = f (z)dz + f (z)dz + |
f (z)dz + |
||
L2 |
BpA |
AN |
NqM |
|
|||
+ |
f (z)dz = 0. |
|
|
MB
Если сложить почленно полученные равенства, то интегралы по линиям AN и BM взаимно уничтожатся, и в результате получим
f (z)dz + f (z)dz + f (z)dz + f (z)dz =
AmB BpA MnN NqM
= |
f (z)dz + |
f (z)dz = 0, |
C0 |
C1 |
|
что и требовалось доказать. |
|
|
Если интеграл от функции |
f (z) по любому замкнутому |
|
контуру, расположенному в области D, равен нулю, то этот интеграл по любой кривой, расположенной внутри области D, не зависит от вида этой кривой, а зависит только от положения начальной и конечной точек этой кривой. Теорема Коши для простого контура гласит, что если функция f (z) аналитична в односвязной области
D, то интеграл по любому замкнутому контуру, лежащему в этой области, равен нулю, и, следовательно, интеграл по любой кривой, соединяющей две точки области D, не зависит от вида кривой, а зависит только от положения этих точек. Поэтому при обозначении интеграла нет необходимости указывать вид кривой, а достаточно указать начальную и конечную точки интегрирования, употребляя обозначение
z2
f (z)dz .
z1
Легко доказать, что в этом случае справедлива формула Ньютона - Лейбница
49
