
Методическое пособие 582
.pdf
z2
f (z)dz = F(z2) - F(z1) = F(z) |
zz2 , |
(1.59) |
|
1 |
|
z1
где F(z) - первообразная для функции f (z) .
Заметим, что правила интегрирования функций комплексного переменного ничем не отличаются от правил интегрирования функций действительного переменного.
2 i
Пример. Вычислить (3z2+2z)dz.
1 i
Так как функция f (z) = 3z2+2z аналитична всюду, то для
вычисления интеграла можно использовать формулу (1.59). В результате получаем, что
2 i |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(3z2+2z)dz = (z3+z2) |
12 |
ii = (2+i)3 +(2+i)2 –- (1-i)3 - (1-i)2 = =7+19i. |
||||||
1 i |
|
|
|
|
|
|
|
|
1.11. Интегральная формула Коши |
||||||||
Теорема. Если функция |
f (z) |
аналитична в замкнутой об- |
||||||
ласти D, ограниченной простым контуром C, то в любой внутрен- |
||||||||
ней точке области D значение функции |
f (z) |
определяется по фор- |
||||||
муле |
|
|
|
|
|
|
|
|
|
|
f (z) |
1 |
|
f ( |
)d |
. |
(1.60) |
|
|
|
|
|
|
|||
|
|
|
2 i C |
|
z |
|
||
Доказательство. Пусть z - любая внутренняя точка области D. Обозначим через C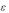 окружность радиуса
окружность радиуса 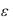 с центром в точке z, а через D
с центром в точке z, а через D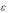 - область, ограниченную этой окружностью. Радиус
- область, ограниченную этой окружностью. Радиус 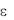 окружности C
окружности C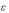 выберем настолько малым, чтобы окружность C
выберем настолько малым, чтобы окружность C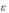 состояла из внутренних точек области D (рис. 1.21). В области D рассмотрим вспомогательную функцию
состояла из внутренних точек области D (рис. 1.21). В области D рассмотрим вспомогательную функцию
50

|
f ( ) |
f (z) |
, |
если z, |
|
( ) = |
|
z |
|||
|
|
|
|||
f '(z), |
если |
z. |
|||
|
|||||
Функция ( ) аналитична и, следовательно, непрерывна во всех точках области D, кроме точки =z. Так как, кроме того,
lim |
= lim |
f ( ) f (z) |
|
z |
|||
z |
z |
Рис.1.21
= f (z),
(z),
то функция ( ) непрерывна и в точке z. Из непрерывности функции ( ) в замкнутой ограниченной области D следует ее ограниченность в этой области:  ( )
( ) k.
k.
Так как функция ( ) аналитична в области D-D , то по теореме Коши для сложного контура
( )d = |
( )d . |
(1.61) |
C |
C |
|
Оценим интеграл, стоящий в правой части равенства (1.61). Так как  ( )
( ) k, то
k, то  ( )d
( )d k2
k2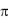 , где >0 - сколь угодно ма-
, где >0 - сколь угодно ма-
C
лое число. Левая часть равенства (1.61) - постоянное число, не зависящее от , а правая часть по модулю меньше любого, сколь угодно малого положительного числа. Это возможно только в том случае, когда
( )d |
= |
( )d = 0, то есть |
|
f ( ) f (z) |
d = 0, |
|
|
||||
C |
C |
|
C |
z |
|
|
|
|
|||
51
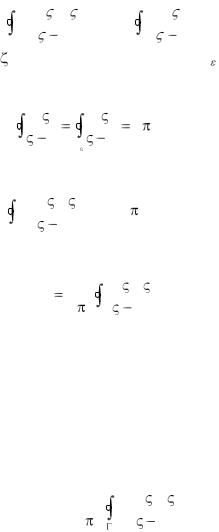
откуда находим, что |
|
f ( |
)d |
- f (z) |
|
d |
= 0. |
|
|
|
|
|
|||
C |
z |
C |
z |
||||
|
|
|
|
|
|||
Так как функция 1/( -z) аналитична в области D-D , то по теореме Коши для сложного контура
|
|
|
|
d |
|
|
|
d |
|
2 i . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
C |
|
|
z |
C |
z |
|||||||
|
|
|
|
|
|
|
|
|
|||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( )d |
|
- f (z) 2 i = 0, |
|||||||
C |
|
|
|
|
z |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (z) |
|
1 |
|
|
f ( )d |
. |
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 i C |
|
z |
|||||
Теорема доказана.
Формула (1.60) называется интегральной формулой Коши. Эта формула показывает, что значения аналитической функции во внутренних точках области D однозначно определяются значениями этой функции в граничных точках этой области.
Доказанная теорема верна также для функций, аналитических в замкнутой области D, ограниченной сложным контуром Г. В этом случае интегральная формула Коши имеет вид
f (z) = |
1 |
|
f ( )d |
. |
(1.62) |
2 i |
|
|
|||
|
|
z |
|
||
Доказательство этой формулы ничем не отличается от доказательства равенства (1.60).
1.12. Интегральная формула Коши для производных от аналитической функции
52
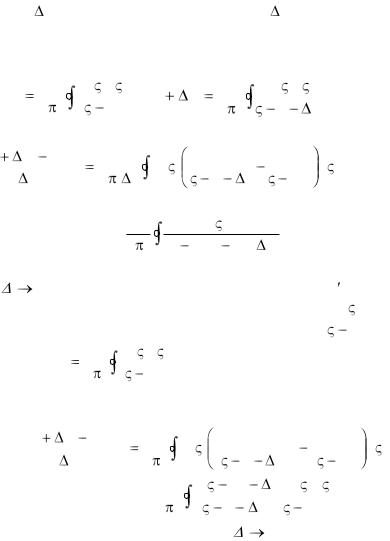
Пусть функция f (z) аналитична в замкнутой области D, ограниченной контуром C, и пусть z – внутренняя точка области D. Выберем z таким образом, чтобы точка z + z принадлежала окрестности точки z, состоящей из точек области D. Тогда, в силу
(1.60)
|
f (z) |
|
1 |
|
|
f ( )d |
, f (z |
z) |
|
1 |
|
|
|
f ( )d |
|
|
|
|||||||
2 |
i C |
|
z |
2 |
i |
|
z |
z |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (z |
z) f (z) |
1 |
|
f ( |
) |
|
1 |
|
|
|
1 |
|
|
|
d |
= |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
z |
|
|
|
|
2 i |
z |
|
|
z |
|
z |
|
z |
|
|
|
||||||
1f ( )d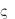
=2 i C (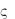 z)(
z)(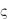 z
z  z) .
z) .
При z 0 левая часть этого равенства стремится к f (z), а подын- |
|||
тегральная функция в правой части стремится к |
f ( |
) |
. Таким |
|
|
||
( |
z)2 |
||
образом, f ' (z) |
1 |
|
f ( |
)d |
|
|
|
|
|
. |
|
2 i |
C |
( |
z)2 |
||
|
|
|
|
|
|
Аналогично,
|
f ' (z |
z) f ' (z) |
|
|
1 |
|
f ( ) |
|
|
1 |
1 |
d = |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
z |
|
2 i |
C |
( |
z |
z)2 |
|
( z)2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(2 |
|
2z |
z) f ( )d |
|
||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
. |
|
|||
|
|
|
|
2 i |
C |
( |
|
z |
z)2 ( |
z)2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда, переходя к пределу при z |
0, получаем, что |
||||||||||||||||
|
|
|
|
|
|
|
|
|
53 |
|
|
|
|
|
|
|
|
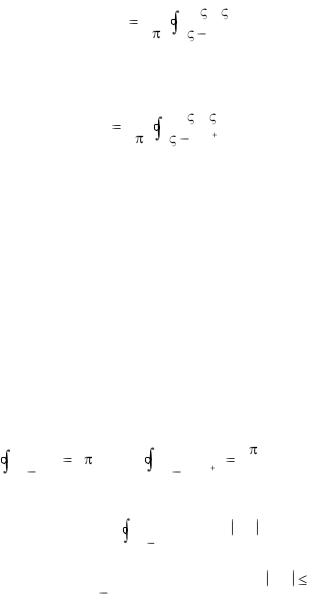
f " (z) |
2! f ( |
)d |
|||
|
|
|
|
. |
|
2 i |
C |
( |
z)2 |
||
|
|
|
|
|
|
Продолжая этот процесс, можно доказать, что функция f (z)
во всех внутренних точках области D имеет производные любого порядка и что
f ( n ) (z) |
n! |
|
|
f ( )d |
. |
(1.63) |
|
|
|
|
|
||||
2 i |
C |
( |
z)n 1 |
||||
|
|
|
|||||
|
|
|
|
|
|
Формула (1.63) также называется интегральной формулой Коши для производных от аналитической функции. Из определения аналитичности функции в точке следует, что если функция f (z) ана-
литична в точке z, то она аналитична и в некоторой окрестности этой точки. Отсюда и из предыдущих рассуждений вытекает следующее утверждение.
Если функция f (z) аналитична в точке z, то она имеет в
этой точке производные любого порядка. Для функций действительного переменного подобное утверждение неверно: функция f (x) может иметь в окрестности точки x производную первого
порядка и не иметь производные более высоких порядков. Интегральные формулы (1.60) и (1.63) можно ис-пользовать
для вычисления контурных интегралов. Для этого формулы (1.60) и (1.63) запишем в виде
|
f (z)dz |
2 if (z0 ) , |
|
|
f (z)dz |
|
2 i |
f |
( n ) |
(z0 ) . (1.64) |
|||||
|
z |
z |
|
|
(z |
z |
|
) |
n 1 |
|
n! |
|
|||
C |
0 |
|
C |
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Примеры: 1) Вычислить |
|
ez2 dz |
, где C: z-2 |
= 3. |
||
C |
z2 |
6z |
||||
|
|
|
|
|
|
|
Так как функция f (z) = |
ez2 |
аналитична в круге |
z-2 3, |
|||
z 6 |
||||||
то по первой формуле (1.64) находим, что
54

|
ez2 dz |
|
|
|
e z2 |
|
|
|
ez2 |
|
|
|
|||
|
|
|
|
z |
6 |
|
dz = 2 i |
|
i |
||||||
|
|
|
|
= |
|
|
|
|
|
|
|
z 0 |
|
. |
|
C |
z2 |
6z |
с |
|
z |
|
|
z 6 |
3 |
||||||
2) Вычислить |
|
|
sin z |
dz, где C - любой контур, |
|||||||||||
|
|
||||||||||||||
C |
( z )4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
содержащий точку z = .
С помощью второй формулы (1.64) при n=3 находим, что
|
sin z |
|
dz=(2 i/3!)(sinz)(3) |
z= =( i/3)(-cosz) z= |
= i/3. |
|
|
|
|
|
|||
|
( z |
) |
4 |
|||
C |
|
|
|
|
||
|
|
|
|
|
|
|
1.13. Степенные ряды в комплексной области
Рассмотрим снова степенной ряд
f (z) = c0 + c1z + c2z +...+ cnzn + ... |
(1.65) |
Как отмечалось ранее в п. 1.4, степенной ряд (1.65) схо-дится в некотором круге радиуса R с центром в начале координат. Для степенных рядов в комплексной области справедливы все основные теоремы о степенных рядах в действительной области. В частности, если радиус сходимости ряда (1.65) R > 0, то сумма этого ряда в любой точке круга сходимости z < R имеет производные любого порядка, каждую из которых можно получить почленным дифференцированием ряда (1.65) соответствующее число раз. Ряды, полученные почленным дифференцированием ряда (1.65), имеют один и тот же радиус сходимости R.
< R имеет производные любого порядка, каждую из которых можно получить почленным дифференцированием ряда (1.65) соответствующее число раз. Ряды, полученные почленным дифференцированием ряда (1.65), имеют один и тот же радиус сходимости R.
Таким образом, если радиус сходимости ряда (1.13) R>0, то сумма этого ряда f(z) является аналитической функцией в круге z
< R.
Рассмотрим теперь степенной ряд вида
55

f (z) = c0+c1(z-z0)+c2(z-z0)2+ ...+cn(z-z0)n +... (1.66)
Если в этом ряде сделать замену переменной z-z0 = , то получим ряд
c0 + c1 + c2 |
2 + ...+ cn |
n + . . . |
(1.67) |
рассмотренного вида (1.65). Пусть ряд (1.67) сходится в круге
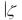 <R, где R>0. Тогда ряд (1.66) сходится в круге z-z0
<R, где R>0. Тогда ряд (1.66) сходится в круге z-z0 < R и сумма ряда (1.66) аналитична в этом круге.
< R и сумма ряда (1.66) аналитична в этом круге.
Рассмотрим еще ряд вида
f (z) |
c 1 |
|
|
c 2 |
|
|
... |
|
c |
n |
|
|
.... |
(1.68) |
||
z z |
0 |
|
(z z |
0 |
)2 |
(z z |
0 |
)n |
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если в этом ряде сделать замену переменной |
|
|
1 |
|
|
, то снова |
||||||||||
|
|
|
|
|
|
|||||||||||
|
z |
|
|
z0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получим ряд вида (1.65). Если этот ряд сходится в круге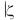
 < R, где R > 0, то ряд (1.68) сходится в области, для которой 1/ z-z0
< R, где R > 0, то ряд (1.68) сходится в области, для которой 1/ z-z0 < R, то есть в области z-z0
< R, то есть в области z-z0 > r, где r = 1/R. Область z-z0
> r, где r = 1/R. Область z-z0 > r представляет собой внешность круга радиуса r с центром в точке z0 . Сумма ряда (1.68) является аналитической функцией в области z-
> r представляет собой внешность круга радиуса r с центром в точке z0 . Сумма ряда (1.68) является аналитической функцией в области z-
z0 > r.
> r.
Наконец, рассмотрим степенной ряд
f (z) = |
ck (z z0 )k + |
ck (z z0 )k , |
(1.69) |
k |
0 |
k 1 |
|
содержащий отрицательные и неотрицательные степени разности z-z0 . Представим сумму ряда (1.69) в виде
f(z) = f1(z)+f2(z),
где
56

f1(z) = |
ck (z z0 )k , f2(z) = |
ck (z z0 )k . |
k |
0 |
k 1 |
Пусть первый из этих рядов сходится в круге z-z0 < R, а второй - вне круга z-z0
< R, а второй - вне круга z-z0 > r. Если r < R, то ряд (1.69) сходится в области r< z-z0 <R, то есть в области, заключенной между двумя концентрическими окружностями с центром в точке z0. Будем называть эту область кольцом. Сумма ряда (1.69) аналитична в этом кольце.
> r. Если r < R, то ряд (1.69) сходится в области r< z-z0 <R, то есть в области, заключенной между двумя концентрическими окружностями с центром в точке z0. Будем называть эту область кольцом. Сумма ряда (1.69) аналитична в этом кольце.
Заметим, что возможен случай, r=0. В этом случае область 0
<z-z0 < R представляет собой круг с исключенной точкой z0.
< R представляет собой круг с исключенной точкой z0.
1.14.Ряды Тейлора и Лорана
Впредыдущем пункте показано, что если степенные ряды
(1.66) и (1.69) сходятся соответственно в круге z-z0 < R или в кольце r< z-z0 <R, то суммы этих рядов аналитичны в области сходимости этих рядов. Оказывается, справедливы и обратные теоремы.
< R или в кольце r< z-z0 <R, то суммы этих рядов аналитичны в области сходимости этих рядов. Оказывается, справедливы и обратные теоремы.
Теорема 1 (теорема Тейлора). Если функция f (z) аналитич-
на в круге z-z0 < R, то в любой внутренней точке z этого круга функция f (z) разлагается в степенной ряд вида
< R, то в любой внутренней точке z этого круга функция f (z) разлагается в степенной ряд вида
f (z) |
= |
|
|
|
ck (z |
|
z0 )k , |
(1.70) |
||
|
|
k |
0 |
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
ck = |
1 |
|
|
|
f (z)dz |
, |
(1.71) |
|||
|
|
|
|
|
|
|
||||
2 |
i |
C |
(z z |
0 |
)k 1 |
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||
а C – окружность z-z0 = R2 < R. |
|
|
|
|
|
|
||||
Доказательство. Пусть |
z |
- |
|
любая внутренняя точка круга. |
||||||
|
|
|
|
|
Проведем окружность C1: z- |
|||||
|
|
|
|
|
z0 = R1, где R1 < R, таким об- |
|||||
|
|
|
|
|
разом, чтобы точка z оказалась |
|||||
|
|
|
|
|
внутри круга z-z0 |
< R1 (рис. |
||||
57
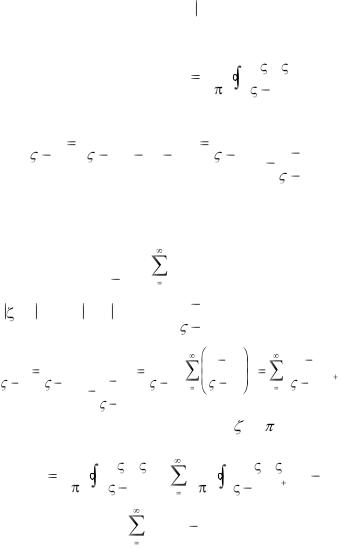
1.22). Так как функция f (z) аналитична в замкнутом круге z-z0 < R1, то по интегральной
< R1, то по интегральной
|
формуле Коши |
|
||||
Рис.1.22 |
|
|
|
|
|
|
f (z) |
1 |
|
f ( )d |
. |
(1.72) |
|
|
|
|
|
|||
|
|
2 i C |
z |
|
||
Функцию
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z ( |
z |
0 |
) (z z |
0 |
) |
|
z |
0 |
1 |
z z0 |
|
|||
|
|
|
|
|
|
|
|
z0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разложим в степенной ряд по степеням z-z0, пользуясь формулой для суммы геометрического ряда
|
|
|
|
|
|
|
|
|
|
a |
= |
|
|
aqk , если |
|
q |
|
< 1. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
q |
k 0 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как -z0 |
= R1, |
|
z-z0 |
< R1, то |
|
z z0 |
|
< 1, следовательно, |
|
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
)k |
|
||||
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
z z |
0 |
|
|
|
|
|
(z z |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
.(1.73) |
||
|
z |
|
z |
|
1 |
z z0 |
|
|
z |
0 k 0 |
|
|
|
z |
|
|
|
k 0 |
( |
z |
)k 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умножим обе части равенства (1.73) на f( )/(2 i) и проинтегрируем полученное равенство по контуру C1. В результате получим,
что f (z) |
1 |
|
f ( )d |
= |
|
1 |
|
|
f ( )d |
(z z |
|
)k = |
|
2 i C |
z |
k 0 2 i C1 ( |
z0 )k 1 |
0 |
|||||||||
|
|
|
|
||||||||||
= |
ck (z z0 )k , |
k |
0 |
где
58
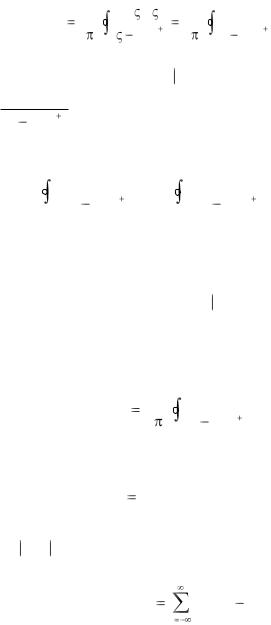
ck |
1 |
|
|
f ( )d |
|
1 |
|
f (z)dz |
. |
2 i C |
( |
z0 )k 1 |
|
2 i C |
(z z0 )k 1 |
||||
|
1 |
|
1 |
|
|||||
Пусть C - любая окружность z-z0 = R2, где R2<R. Так как
= R2, где R2<R. Так как
f (z)
функция (z z0 )k 1 аналитична в замкнутой области, лежащей ме-
жду окружностями C и C1 , то по теореме Коши для сложного контура
|
f (z) |
dz = C |
f (z) |
dz . |
|
|
|
||
C |
(z z0 )k 1 |
(z z0 )k 1 |
||
1 |
|
|
|
|
Таким образом, для вычисления коэффициентов ck можно использовать формулу (1.71), где C - любая окружность с центром в точке z0 радиуса R2<R.
Теорема доказана.
Если функция f (z) аналитична в круге z-z0 < R, то она имеет
< R, то она имеет
производные любого порядка во всех внутренних точках этого круга, причем справедлива формула (1.63). В частности, для точки z = z0 эта формула имеет вид
f |
( k ) |
(z0 ) |
k! |
|
|
f (z)dz |
||||
|
|
|
|
|
|
|
|
. |
||
|
2 i |
|
(z |
z |
|
) |
k 1 |
|||
|
|
|
C |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что коэффициенты ck ряда Тейлора можно вычислять по формулам
c |
|
f (k ) (z |
0 |
) |
. |
(1.74) |
k |
k! |
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
Теорема 2 (теорема Лорана). Если функция |
f (z) аналитична |
|||||
в кольце r< z-z0 <R, то в любой внутренней точке z этого кольца функция f (z) разлагается в степенной ряд вида
f (z) |
c |
k |
(z |
z |
0 |
)k , |
(1.75) |
|
|
|
|
|
|
k
где
59
