
Методическое пособие 582
.pdf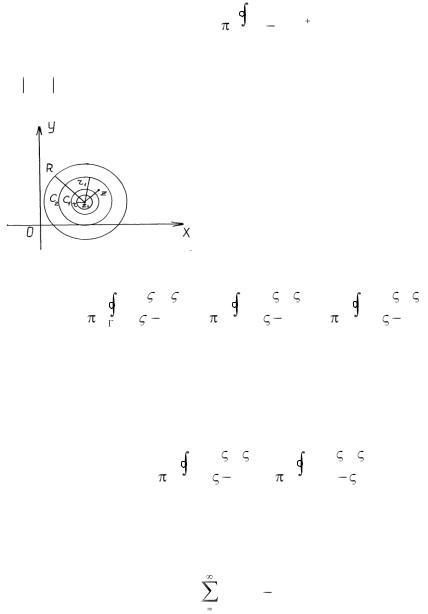
|
|
|
|
ck |
= |
1 |
|
|
f (z)dz |
|
. |
|
|
(1.76) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 i |
C |
(z z |
0 |
)k |
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Пусть z – любая точка кольца |
|
|
|
||||||||||||||||||||||
r < z-z0 |
< R. Проведем две окружности C1 |
и C2 радиуса R1 |
|
||||||||||||||||||||||
и R2 (r < R1 < R2 < R) таким образом, чтобы точка z принад- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
лежала области, заключенной меж- |
||||||||||||||||||
|
|
|
|
|
|
|
ду окружностями C1 и С2 (рис.1.23). |
||||||||||||||||||
|
|
|
|
|
|
|
Так как функция f (z) аналитична в |
||||||||||||||||||
|
|
|
|
|
|
|
замкнутой |
|
|
области, заключенной |
|||||||||||||||
|
|
|
|
|
|
|
между окружностями C1 |
и С2, то по |
|||||||||||||||||
|
|
|
|
|
|
|
интегральной |
формуле |
Коши |
для |
|||||||||||||||
|
|
|
|
|
|
|
многосвязной области |
|
|
|
|||||||||||||||
|
Рис.1.22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (z) |
= |
1 |
|
f ( )d |
|
= |
|
1 |
|
|
|
f ( )d |
|
+ |
|
1 |
|
|
f ( )d |
|
, |
||||
2 i |
z |
2 i C |
2 |
|
z |
|
|
|
2 i C |
z |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
где интегрирование по окружности C2 проводится против часовой стрелки, а по окружности C1 - по часовой стрелке. Если интегрирование по окружности C1 изменить на противоположное, то предыдущая формула примет вид
f (z) = |
1 |
|
|
|
f ( )d |
+ |
1 |
|
|
f ( )d |
= |
|
2 |
i C |
2 |
|
z |
2 |
i C |
z |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|||
|
|
= f2 (z) + |
f1 (z) . |
|
|
|
(1.77) |
|||||
Так же, как в теореме 1, доказывается, что
f |
2 |
(z) = |
c |
k |
(z z |
0 |
)k , |
|
|
|
|
|
|||
|
|
k |
0 |
|
|
|
|
60
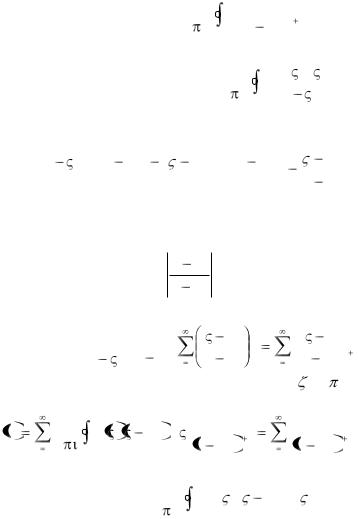
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ck |
= |
1 |
|
|
|
|
|
|
|
f (z)dz |
|
|
|
. |
(1.78) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
i |
C |
2 |
|
(z |
z0 )k |
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим функцию |
f1 (z) |
= |
1 |
|
|
|
|
f ( |
)d |
. |
|
|
|||||||||||||||
|
2 i |
C |
|
|
|
z |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Функцию |
1 |
= |
|
|
1 |
|
|
|
|
|
|
= |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z |
(z z |
0 |
) |
( |
|
z |
0 |
) |
|
z |
z |
0 |
1 |
|
|
|
|
z0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
z0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
разложим в степенной ряд по степеням z-z0, пользуясь формулой для суммы геометрического ряда. Так как
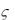 z0 <1, z z0
z0 <1, z z0
то
1 |
1 |
|
|
z0 |
n |
( |
z0 )n |
|
|||
|
|
|
|
||||||||
|
= |
|
|
|
|
|
|
|
|
. |
(1.79) |
z |
z |
z0 n o z z0 |
|
n 0 (z |
z0 )n 1 |
||||||
Если обе части равенства (1.79) умножить на f( )/(2 i) и проинтегрировать полученное равенство по контуру C1, то получим, что
|
1 |
|
|
n |
|
1 |
|
cn |
|
f1 z |
|
|
f |
z0 |
d |
|
|
|
, |
2 C |
n 1 |
n 1 |
|||||||
n 0 |
|
|
|
z z0 |
n 0 z z0 |
||||
|
1 |
|
|
|
|
|
|
|
|
где c |
|
= |
1 |
f ( )( z |
|
)n d . |
|
n |
|
0 |
|||||
2 i |
|||||||
|
|
|
|
||||
|
|
|
C |
|
|
||
|
|
|
|
1 |
|
|
Если в полученных равенствах сделать замену n+1 = -k, то эти равенства примут вид
61
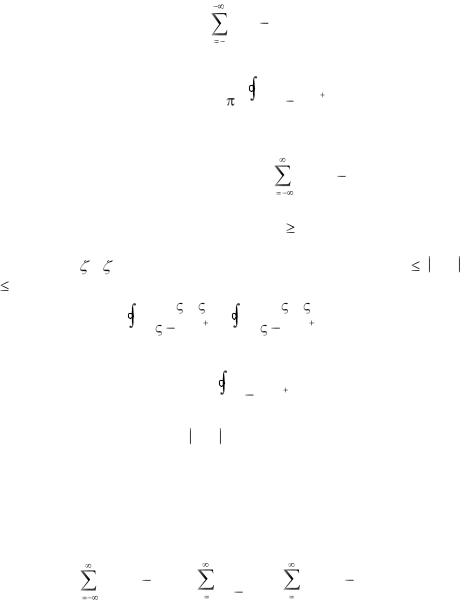
f |
1 |
(z) = |
c |
k |
(z z |
0 |
)k , |
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
k |
1 |
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
ck = |
1 |
|
|
|
|
f (z)dz |
. |
(1.80) |
|
|
|
2 i |
C |
2 |
(z |
z0 )k 1 |
|||||
|
|
|
|
|
|||||||
Из равенств (1.78) и (1.80) находим, что |
|
|
|||||||||
f (z) = f1 (z) + f2 (z) = |
|
ck (z z0 )k . |
|
||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
Коэффициенты ck этого ряда при k<0 и k |
0 вычисляются с помо- |
||||||||||
щью интегралов по разным окружностям C1 и C2. Однако, так как |
|||||||||||
функция f( )/( -z0)k+1 аналитична в замкнутой области R1 |
z-z0 |
||||||||||
R2, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( |
(d |
= C |
|
|
|
f ( |
(d |
=, |
|||||
|
|
|
|
|
|
|
|
|
|
|||||
C |
( |
z0 )k 1 |
2 |
( |
|
|
z0 )k 1 |
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
f (z)dz |
|
|||||
|
|
= |
|
|
|
|
|
|
|
, |
|
|||
|
|
C |
|
(z |
|
z |
0 |
)k 1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где C - любая окружность |
z-z0 |
|
= R3, где r < R3 < R. |
|||||||||||
Таким образом, формула (1.76) для вычисления коэффициентов ряда (1.75) справедлива для любых целых k.
Теорема доказана.
Ряд, стоящий в правой части равенства (1.75), называется рядом Лорана. Представим ряд Лорана в виде суммы двух рядов:
c |
|
(z z |
|
)k = |
|
ck |
|
|
+ |
c |
|
(z z |
|
)k . |
|
k |
0 |
k 1 (z |
z) |
k |
k |
0 |
|||||||||
|
|
|
|
|
|
|
|||||||||
k |
|
|
|
|
|
|
k 0 |
|
|
|
|
||||
62
Ряд |
|
ck |
|
называется главной частью, а ряд |
(z |
|
z)k |
||
k 1 |
|
|
ck (z z0 )k – правильной частью ряда Лорана.
k 0
1.15. Особые точки функции комплексного переменного. Классификация особых точек
Точка z0 называется изолированной особой точкой функции f (z) , если функция f (z) не аналитична в точке z0, но аналитична
в некоторой окрестности этой точки. Так как в настоящем пособии не рассматриваются особые точки других типов, то изолированные особые точки будем называть просто особыми точками.
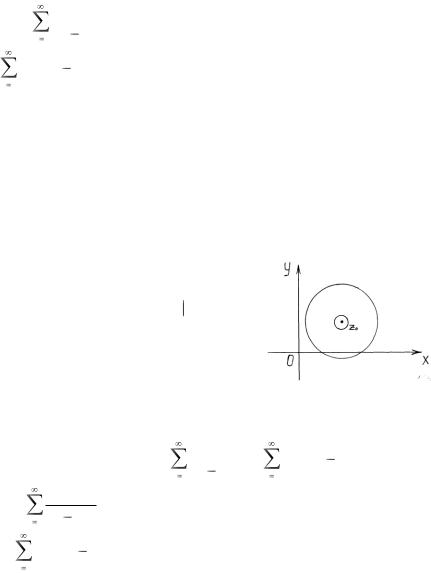
Пусть z0 - особая точка функции f (z) , и пусть функция
f (z) аналитична в круге z-z0 < R с исключенной точкой z0 (рис. 1.24). Тогда функция f (z) в окре-
< R с исключенной точкой z0 (рис. 1.24). Тогда функция f (z) в окре-
стности точки z0 разлагается в ряд Лорана
|
|
|
|
|
|
|
Рис.1.24 |
|
||||
f (z) = |
|
ck |
|
|
+ |
c |
|
(z |
z |
|
)k , |
(1.81) |
|
|
|
k |
k |
0 |
|||||||
k 1 (z |
|
z) |
|
|
|
|
|
|
||||
|
|
|
k 0 |
|
|
|
|
|
|
|||
где k 1 (z ckz)k – главная часть,
аck (z z0 )k – правильная часть ряда Лорана.
k 0
Возможны следующие случаи:
1. Все коэффициенты главной части ряда Лорана равны нулю, то есть разложение (15.1) имеет вид
63

f(z) = c0 + c1(z-z0) + c2(z-z0)2 +... .
Вэтом случае точка z0 называется устранимой особой точкой функции f (z) . Если функцию f (z) определить в точке z0, поло-
жив f (z0 ) lim f (z) c0 , то особенность функции в точке z0 уст-
z z0
раняется. Определенная таким образом функция f (z) становится не только непрерывной, но и аналитической в точке z0. Например,
точка z0=0 кажется особой для функции f (z) = |
sin z |
. Однако раз- |
|||||||||
z |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
ложение функции |
sin z |
по степеням z имеет вид |
|
||||||||
z |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
sin z |
|
z2 |
|
z4 |
|
||||
|
|
|
|
= 1 |
|
|
|
.... . |
|
|
|
|
|
|
z |
3! |
5! |
|
|
||||
|
|
|
|
|
|
|
|||||
Все коэффициенты главной части ряда Лорана равны нулю. Поэтому, точка z0=0 является устранимой особой точкой для функции
f (z) = |
sin z |
. Если положить f(0) = |
lim |
sin z |
=1, |
|
|
|
z |
z |
|
|
|||||
|
|
z z0 |
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
sinz |
, если |
z 0, |
|
то особая точка z0 =0 устраняется. |
f (z) |
z |
|
|
||||
1, если z |
0 |
|||||||
|
|
|
|
|
||||
аналитична на всей плоскости комплексного переменного.
2. Все коэффициенты ряда Лорана, кроме конечного числа,
равны нулю, ряд Лорана (1.81) для функции |
f (z) имеет вид |
||||||||||
f (z) = |
c n |
|
|
|
c n 1 |
|
.... |
c 1 |
|
|
c0 c1 (z z0 ) .... , (1.82) |
(z z |
|
)n |
|
(z z |
)n |
z z |
|
|
|||
|
|
0 |
|
0 |
|
|
|
0 |
|
|
|
где c-n 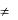 0. В этом случае точка z0 называется полюсом крат ности n для функции f (z) . Если n = 1, то точка z0 называется простым полюсом.
0. В этом случае точка z0 называется полюсом крат ности n для функции f (z) . Если n = 1, то точка z0 называется простым полюсом.
Если аналитическую функцию f (z) можно представить в ви-
де
f (z) = (z-z0)n g(z), |
(1.83) |
64

где g(z0) 0, |
то точка z0 |
называется нулем функции f(z) крат- |
|||||||||
ности n. |
|
|
|
|
|
|
|
|
|
|
|
Пусть точка z0 - полюс кратности n для функции |
f (z) . За- |
||||||||||
пишем разложение функции f (z) в ряд Лорана (1.82) в виде |
|||||||||||
|
1 |
|
|
(c-n + c-n+1(z-z0) + …+ c0(z-z0)n + ...) = |
|||||||
f (z) = |
|
|
|
||||||||
(z z |
0 |
)n |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
h(z) |
|
, |
(1.84) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
(z z |
0 |
)n |
|||
|
|
|
|
|
|
|
|
|
|
|
|
где h(z0) = c-n |
0. |
|
|
|
|
|
|
|
|
|
|
Отсюда следует, что 1/ f (z) = (z-z0)n/h(z) = (z-z0)ng(z), |
|
||||||||||
где g(z0) = 1/h(z0) = 1/c-n |
0. |
|
|
|
|
|
|||||
Таким образом, если точка z0 – полюс кратности n для функ- |
|||||||||||
ции f (z) , то z0 - нуль кратности n для функции 1/ f (z) . |
|
||||||||||
Справедливо и обратное утверждение: если точка |
z0 - нуль |
||||||||||
кратности n для функции f (z) , то z0 - полюс кратности n |
|
||||||||||
для функции |
f (z) , то z0 - полюс кратности n для функции 1/ f (z) . |
||||||||||
Из равенства (1.84) следует также, что если z0 - полюс любой |
|||||||||||
кратности для функции |
f (z) , то |
|
|
|
|
||||||
lim f (z) = .
zz0
3.Отличны от нуля бесконечное число коэффициентов глав-
ной части ряда Лорана (1.82) для функции f (z) . В этом случае точка z0 называется существенно особой точкой для функции
f (z) .
Пример. Рассмотрим функцию f (z) = sin(1/z) и точку
z0= 0. Разложение функции sin(1/z) в ряд Лорана в окрестности точки z0 = 0 имеет вид
sin(1/z) = |
1 |
- |
1 |
1 |
.... . |
|
|
|
|
|
|||
z |
3! z3 |
5! z5 |
||||
|
|
|
65 |
|
|
|

Ряд, стоящий в правой части этого равенства, является главной частью ряда Лорана для функции sin(1/z). Поэтому точка z0 = 0 является существенно особой точкой для функции sin(1/z).
Можно доказать, что если z0 - существенно особая точка для
функции |
f (z) , |
то lim f (z) не существует. Это означает, что |
|
|
z z0 |
функция |
f (z) |
стремится к различным пределам, когда точка z |
стремится к точке z0 по различным путям.
Заметим, что все определения и классификация особых точек применимы и к бесконечно удаленной точке z = . Точка z = является особой точкой для функции f (z) , если точка z = 0 является
особой точкой для функции f(1/z). Тип особой точки z = для функции f (z) совпадает с типом особой точки z = 0 для функции
f (1/ z) .
Например, точка z=0 является существенно особой точкой для функции sin(1/z). Следовательно, точка z= является существенно особой точкой для функции sinz.
1.16. Вычет функции в особой точке. Основная теорема о вычетах
Пусть z0 - изолированная особая точка функции f (z) ,
С - простой контур, содержащий особую точку z0 и не содержащий других особых точек. Докажем, что  f (z)dz не зависит от вида
f (z)dz не зависит от вида
C
контура C.
Пусть C1 и С2 - простые контуры, содержащие особую точку z0 и не содержащие других особых точек. Возможны два случая:
1. Контуры C1 и C2 не пересекаются (рис. 1.25). Так как функция f (z) аналитична в области, лежащей между контурами C1 и C2, то по теореме Коши для сложного контура
 f (z)dz =
f (z)dz =  f (z)dz .
f (z)dz .
C1 |
C2 |
66
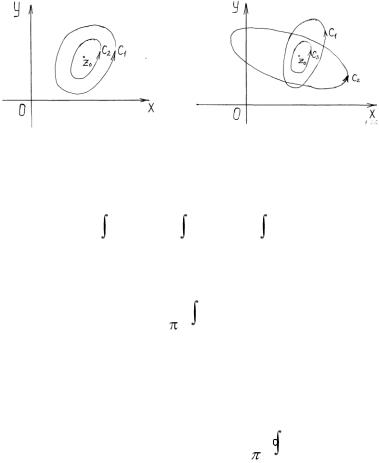
2. Контуры C1 и C2 пересекаются. Проведем контур C3, содержащий точку z0 так, чтобы C3 лежал внутри контуров C1 и C2
(рис. 1.26).
Рис. 1.25 |
Рис. 1.26 |
Тогда, по доказанному,
 f (z)dz =
f (z)dz =  f (z)dz =
f (z)dz =  f (z)dz ,
f (z)dz ,
C1 |
C3 |
C2 |
что и требовалось доказать.
1
Определение. Число 
 f (z)dz , где C – простой кон-
f (z)dz , где C – простой кон-
2 i C
тур, содержащий особую точку z0 и не содержащий других особых
точек, называется вычетом функции |
f (z) |
в особой точке z0 и обо- |
|||
значается символом Re s[ f (z), z0 ] . |
Таким образом, |
по определе- |
|||
нию, |
|
|
|
|
|
Re s[ f (z), z0 ] = |
1 |
f (z)dz , |
(1.85) |
||
2 i |
|||||
|
|
C |
|
||
где C - любой простой контур, содержащий особую точку z0 и не содержащий других особых точек функции f (z) . Определение
вычета корректно, так как интеграл, стоящий в правой части равенства (1.85), не зависит от вида контура C.
67

Если z0 - особая точка функции |
f (z) , то в окрестности точки |
|||||||||||||||
z функция f (z) разлагается в ряд Лорана |
|
|
|
|
|
|
||||||||||
|
|
f (z) |
|
|
|
c |
k |
(z z |
0 |
)k , |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сk |
1 |
|
f (z)dz |
|
|
, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 i |
|
(z |
|
z |
|
) |
k |
1 |
|
||||
|
|
|
|
|
C |
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в частности, если k = -1, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
c 1 |
= |
1 |
|
|
f (z)dz = Re s[ f (z), z0 ] . |
(1.86) |
||||||||||
|
|
|
||||||||||||||
2 i |
|
|||||||||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|||
Роль понятия вычета выясняется из следующей теоремы. Теорема 1 (основная теорема о вычетах). Если функция f (z)
аналитична в замкнутой области D, ограниченной простым контуром C, кроме конечного числа особых точек z1, z2, ..., zn, ни одна из которых не лежит на контуре C, то
|
n |
|
f (z)dz = 2 i |
Re s[ f (z), zk ] . |
(1.87) |
C |
k 1 |
|
Доказательство. Окружим особые точки z1, z2,..., zn контурами C1,C2,..,Cn так, чтобы эти контуры не пересекались между собой и не пересекали контур C
Рис.1.27 (рис. 1.27).
Так как функция f (z) аналитична в замкнутой области, лежащей
между внешним контуром C и внутренними контурами C1, C2,..., Cn, то по теореме Коши для сложного контура, имеем
68

|
n |
n |
1 |
|
|
f (z)dz = |
f (z)dz = 2 i |
|
f (z)dz = |
||
|
|
||||
k 1 2 i |
|||||
C |
k 1 Ck |
Ck |
|||
n
=2 i Re s[ f (z), zk ] ,
k 1
что и требовалось доказать.
Вычет функции в бесконечно удаленной точке
Пусть функция |
f (z) |
аналитична вне круга радиуса R с цен- |
|||||||||||
тром в начале координат. Тогда |
функция |
f (z) в |
области |
||||||||||
z > R разлагается в ряд Лорана |
|
|
|
|
|
|
|
|
|
||||
f (z) |
= |
c |
|
zk , где |
c |
|
= |
1 |
|
f (z)dz |
. |
(1.88) |
|
k |
k |
|
|
|
|||||||||
|
|
|
|
|
|
2 i C |
z |
k 1 |
|
||||
|
k |
|
|
|
|
|
|
|
|
|
|||
Интегралы для вычисления коэффициентов ck ,берутся по окружности C: z = R достаточно большого радиуса R в направлении против часовой стрелки.
= R достаточно большого радиуса R в направлении против часовой стрелки.
Определение. Число |
|
1 |
|
|
f (z)dz , где интегрирование по окруж- |
|||||
|
|
|
|
|||||||
2 i C |
||||||||||
|
|
|
|
|
|
|||||
ности C- |
z = R проводится по часовой стрелке, называет- |
|
||||||||
ся вычетом функции |
f (z) |
в бесконечно удаленной точке и обо- |
||||||||
значается через Re s [ |
f (z) , ]. |
|
||||||||
Из формул (1.88) для ck при k = -1 следует, что |
|
|||||||||
c 1 = |
1 |
|
f (z)dz = - |
1 |
|
|
f (z)dz = - Re s [ f (z) , ]. |
|
||
|
|
|
|
|
|
|||||
|
2 |
i C |
2 i |
C |
|
|||||
Таким образом, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Re s [ f (z) , ]= - c 1 . |
(1.89) |
|
Пример. Пусть f (z) = (z+1)/z = 1+1/z. Последнее выражение является разложением функции в ряд Лорана в окрестности беско-
69
