
Методическое пособие 582
.pdf
Таким образом, из предположения о существовании производной f (z) следует выполнение равенств (1.38), то есть условия Коши-Римана необходимы для существования производной f (z).
1) Достаточность. Предположим теперь, что равенства
(1.38) выполнены: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
u(x, y) |
|
|
v(x, y) |
, |
u(x, y) |
v(x, y) |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
|
|
y |
y |
|
|
x |
||||
и докажем, что в этом случае функция |
|
f (z) |
имеет производную |
||||||||||
в точке z= x+iy, то есть предел (1.39) |
|
|
|
|
|||||||||
lim |
|
f (z) |
= lim |
f (z z) |
f (z) |
существует. |
|||||||
|
|
|
z |
|
|
||||||||
z 0 |
z |
z 0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Так как функции u(x,y) и v(x,y) дифференцируемы в точке M(x,y), то полное приращение этих функций в точке M(x,y) можно представить в виде
u(x, y) |
|
|
u(x, y) |
x |
|
|
u(x, y) |
y |
1 x |
2 y , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
y |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
v(x, y) |
|
|
v(x, y) |
x |
|
|
|
v(x, y) |
y |
x |
y , |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
y |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где 1 0, 2 0, 1 |
0, |
|
2 0 при x |
0, |
y 0. |
|
||||||||||||
Так как, в силу (1.38), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
u(x, y) |
|
|
v(x, y) |
|
, |
|
u(x, y) |
|
v(x, y) |
, |
|||||||
|
|
x |
|
|
|
y |
|
|
y |
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x, y) |
|
|
u(x, y) |
x |
|
|
|
v(x, y) |
y |
x |
y , |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
|
|
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
30

|
v(x, y) |
|
|
|
v(x, y) |
|
|
x |
|
|
|
|
u(x, y) |
y |
|
x |
|
|
|
|
y . |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f (z) |
u(x, y) i v(x, y) |
( |
|
|
u(x, y) |
|
|
x |
|
|
v(x, y) |
|
y) |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ i( |
v(x, y) |
|
|
x |
|
|
|
u(x, y) |
|
|
y) ( |
|
i ) x ( |
i ) y = |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= u(x, y) |
|
|
|
|
u(x, y) |
|
x |
|
|
u(x, y) |
y |
|
|
1 x |
2 y |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
( |
|
u (x, y) |
i |
|
v (x, y) |
)( x i y) ( |
i ) x ( |
|
|
i |
) y = |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
= ( |
u(x, y) |
|
i |
|
v(x, y) |
) z |
|
|
x |
|
|
y , |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = |
1+i |
1 |
0, |
|
2 = |
|
|
2+i |
2 |
|
0 при |
z = |
x+i |
|
y |
|
0. |
|
|
|||||||||||||||||||||||||||
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
f (z) |
|
|
|
|
|
u(x, y) |
|
i |
v(x, y) |
|
|
|
x |
|
|
|
|
y |
. |
(1.42) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
z |
|
|
|
z |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Так как |
|
z |
|
2 = |
|
|
|
|
x |
2+ |
|
|
|
y 2, то |
|
|
|
x/ z |
1, |
|
|
y/ z |
|
1. Поэто- |
||||||||||||||||||||||
му |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
0 |
|
|
|
при |
z |
|
|
0. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что правая часть равенства (1.42) имеет предел при z 0, следовательно, и левая часть имеет предел при z 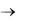
31
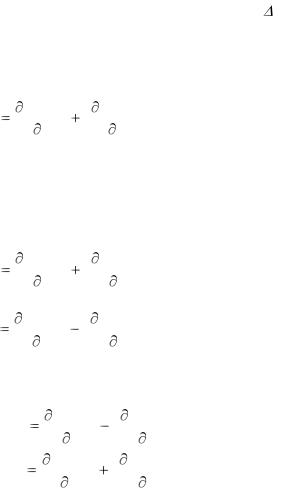
0, причем этот предел не зависит от того, по какому пути z стремится к 0. Таким образом, доказано, что если в точке M(x,y)
выполнены условия (1.38), то функция |
f (z) имеет производную |
||||||
в точке z = x+iy, причем |
|
|
|
|
|
|
|
|
df (z) |
|
u(x, y) |
i |
|
v(x, y) |
. |
|
|
|
|
|
|
||
|
dz |
|
x |
|
|
x |
|
Теорема доказана полностью.
В процессе доказательства теоремы получены две формулы (1.40) и (1.42) для производной от функции комплексного переменного
|
df (z) |
|
u(x, y) |
i |
v(x, y) |
, |
||
|
dz |
|
x |
x |
||||
|
|
|
|
|
|
|||
df (z) |
|
v(x, y) |
i |
|
u(x, y) |
. |
||
|
|
|
|
|
|
|||
|
dz |
|
y |
|
|
y |
|
|
С помощью формул (1.38) можно получить еще две формулы
|
df (z) |
|
|
u(x, y) |
i |
u(x, y) |
, |
(1.43) |
||||
|
dz |
|
|
x |
y |
|||||||
|
|
|
|
|
|
|
|
|||||
df (z) |
|
|
v(x, y) |
i |
|
v(x, y) |
. |
(1.44) |
||||
|
|
|
|
|
|
|
|
|
||||
|
dz |
|
|
y |
|
|
x |
|
|
|
||
Если функция f(z) имеет производную во всех точках области D, то говорят, что функция f (z) дифференцируема в области D.
Для этого необходимо и достаточно, чтобы условия КошиРимана выполнялись во всех точках области D.
Пример. Проверить условия Коши-Римана для функции ez.
32
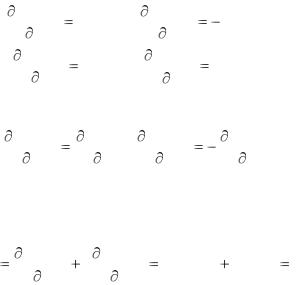
Так как ez= ex+iy = ex(cosy + isiny),
то u(x,y) = Reez = excosy, v(x,y) = Imez = exsiny,
поэтому
|
u(x, y) |
ex cos y , |
|
u(x, y) |
ex sin y |
, |
||
|
|
|
|
|
|
|||
|
x |
|
y |
|||||
|
|
|
|
|
||||
|
v(x, y) |
ex sin y , |
|
v(x, y) |
ex cos y , |
|
||
|
|
|
|
|
|
|
||
|
x |
|
y |
|
||||
|
|
|
|
|
||||
следовательно,
u(x, y) |
|
v(x, y) |
, |
u(x, y) |
|
v(x, y) |
. |
|
|
|
|
|
|||
x |
|
y |
|
y |
|
x |
|
Условия Коши - Римана для функции ez выполнены во всех точках z. Таким образом, функция ez дифференцируема на всей плоскости комплексной переменной, причем
(ez )' |
u(x, y) |
i |
v(x, y) |
ex (cos y i sin y) ez . |
|
x |
x |
||||
|
|
|
Точно так же доказывается дифференцируемость функций zn, cosz, sinz, chz, shz, Lnz, и справедливость формул
(zn) = n zn-1 , (cosz)
= n zn-1 , (cosz) = -sinz, (sinz)
= -sinz, (sinz) = cosz,
= cosz,
(chz) = shz, (shz)
= shz, (shz) = chz, (Lnz)
= chz, (Lnz) = 1/z.
= 1/z.
Для функций комплексного переменного остаются в силе все правила дифференцирования функций действительного переменного. Доказательство этих правил вытекает из определения производной так же, как и для функций действительного переменного.
33

1.7. Аналитические и гармонические функции. Связь между ними
Функция f (z) = u(x,y)+iv(x,y) называется аналитической в точке z = x+iy, если она имеет производную в точке z и в некоторой окрестности этой точки. Функция f (z) называется аналити-
ческой в области D, если она аналитична в каждой точке этой области, иначе говоря, если во всех точках области D выполняются условия Коши – Римана
u(x, y) |
|
v(x, y) |
, |
u(x, y) |
|
v(x, y) |
. |
|
|
|
|
|
|||
x |
|
y |
|
y |
|
x |
|
Функция u(x,y) называется гармонической в области D, если она имеет в области D непрерывные производные до второго порядка включительно и если
|
|
|
|
2u( x, y) |
2u( x, y) |
= 0. |
(1.45) |
||||
|
|
|
|
x2 |
|
|
y 2 |
||||
|
|
|
|
|
|
|
|
||||
Выражение |
2u( x, y) |
|
2u( x, y) |
|
называется оператором Лап- |
||||||
x2 |
y 2 |
||||||||||
|
|
|
|
|
|
||||||
ласа и обозначается через u(x, y) , так что уравнение (1.45) |
|
||||||||||
можно записать в виде |
u(x, y) = 0. |
|
|
|
|||||||
Следующие две теоремы устанавливают связь между ана- |
|||||||||||
литическими и гармоническими функциями. |
|
|
|||||||||
Теорема 1. Если функция f (z) |
= u(x,y)+iv(x,y) аналитична |
||||||||||
в области D, то функции u(x,y) и v(x,y) гармоничны в области D.
Доказательство. Так как функция |
f (z) аналитична в об- |
||||||||
ласти D, то во всех точках этой области выполняются условия |
|||||||||
Коши - Римана (1.38) |
|
|
|
|
|
|
|
||
|
u(x, y) |
v(x, y) |
, |
u(x, y) |
|
v(x, y) |
. |
||
|
|
|
|
|
|
|
|||
|
x |
y |
y |
|
x |
||||
34

Предполагая, что функции u(x,y) и v(x,y) имеют в области D непрерывные частные производные до второго порядка включительно, продифференцируем первое из равенств (1.38) по переменной x, а второе - по y и сложим полученные равенства. Получим
2u( x, y) |
|
2u( x, y) |
= |
2u( x, y) |
|
2u( x, y) |
0 . |
x2 |
|
y 2 |
y x |
|
x y |
||
|
|
|
|
Точно так же доказывается гармоничность функции v(x,y). Теорема 2. Если функция u(x,y) гармонична в односвязной области D, то существует аналитическая функция f (z) такая, что
Re f (z) = u(x,y).
Для доказательства этой теоремы достаточно найти функцию v(x,y) такую, чтобы для функции
f (z) = u(x,y)+iv(x,y) в области D выполнялись условия Коши-
Римана (1.38) |
|
|
|
|
|
|
|
|
|
v(x, y) |
|
u(x, y) |
, |
v(x, y) |
|
u(x, y) |
. |
|
x |
|
y |
|
|
|||
|
|
|
y |
|
x |
|||
Эти равенства можно рассматривать как систему дифференциальных уравнений для определения функции v(x,y). Проинтегрируем первое из равенств (1.38) по переменной x в пределах от x0 до x. Получим
x
v(x, y) v(x0 , y) 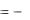
x0
u(x, y) dx , y
отсюда следует, что
x
v(x, y) 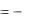
x0
u(x, y)
y dx v( x0 , y) .
Полученное равенство продифференцируем по переменной y. Получим
v(x, y) |
x 2u(x, y) |
dx |
v(x |
0 |
, y) |
. |
(1.46) |
|
|
|
|
|
|
||||
y |
|
y2 |
y |
|
||||
|
|
|
|
|
||||
|
x0 |
|
|
|
|
|
|
|
35

Так как функция u(x,y) гармонична в области D, то
|
|
|
|
|
|
|
|
2u( x, y) |
|
2u( x, y) |
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если в равенстве (1.46) сделать еще замену |
v(x, y) |
u(x, y) |
, |
|||||||||||||||||||||||||||
y |
|
|
|
|
|
x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то это равенство запишется в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
u(x, y) x |
2 u(x, y) |
dx |
|
|
v(x |
0 , y) |
|
u(x, y) |
u(x0 , y) |
|
v(x0 |
, y) |
. |
|
|||||||||||||||
|
|
x |
x0 |
|
x 2 |
|
|
|
y |
|
|
x |
|
|
x |
|
|
|
y |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
v(x0 , y) |
|
u(x0 |
, y) |
, |
|
|
|
|
|
y |
u( x0 , y) |
dy C . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
v( x0 |
, y) |
|
|
|
|
|
|
||||||||||
|
|
|
y |
|
|
|
x |
|
|
|
|
|
|
x |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом,
x |
u( x, y) |
|
|
v( x, y) |
|
dx |
|
y |
|||
x0 |
|
||
|
|
Точно так же доказывается, что
y u( x0 , y) dy C . (1.47)
y0 x
y
v( x, y)
y0
u( x, y) dy x
x u( x, y0 ) dx C . (1.48)
x0 y
С помощью формул (1.47) и (1.48) функция v(x,y), а следовательно, и функция f (z) , определяется с точностью до постоянного
слагаемого.
Теорема доказана.
36
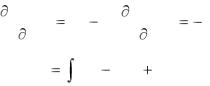
Функции u(x,y) и v(x,y), для которых в области D выполняются условия Коши-Римана (1.38), называются взаимно сопряженными. Зная одну из них, вторая определяется с точностью до постоянного слагаемого.
Пример. Дана гармоническая функция u(x,y) = x2-y2-x. Найти сопряженную ей функцию v(x,y) и аналитическую функцию f (z) = u(x,y)=iv(x,y) при дополнительном условии f(0) = 0.
Для решения этой задачи воспользуемся формулой (1.48), полагая в этой формуле x0=0, y0=0. Так как
|
u(x, y) |
2x 1 |
, |
u(x, y) |
2 y , |
|
|
|
|||
|
x |
y |
|||
|
|
|
|
||
|
|
y |
|
|
|
то |
v(x, y) |
(2x 1)dy C . |
|
||
0
Следовательно,
f (z) = (x2-y2-x) + i(2xy–y+C) = (x+iy)2 - (x+iy) + iC = z2-z+iC.
Из условия f(0) = 0 следует, что C = 0.
Таким образом, v(x,y) = 2xy-y, f(z) = z2–z.
37
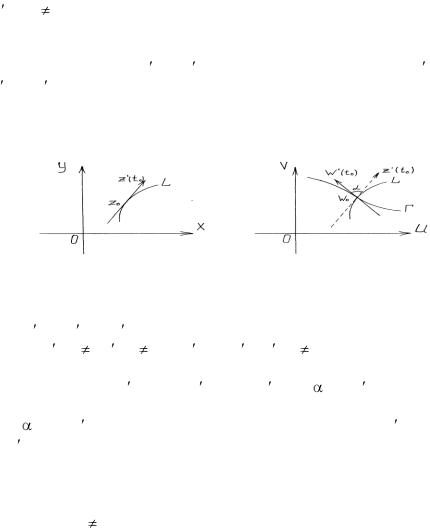
1.8. Геометрический смысл модуля и аргумента производной
от функции комплексного переменного. |
|
Понятие конформного отображения |
|
Пусть функция f (z) аналитична в точке |
z0, причем |
f (z0) ) 0, и пусть z = z(t) = x(t)+iy(t) - уравнение некоторой кривой Г |
|
на плоскости комплексного переменного, причем z0 |
= z(t0). Будем |
предполагать, что функция z(t) имеет в точке t0 производную, отличную от 0: z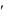 (t0) = x (t0)+iy (t0)
(t0) = x (t0)+iy (t0)  0. Как известно, вектор z (t0) = x (t0)+iy (t0) направлен по касательной к кривой Г в точке z0.
0. Как известно, вектор z (t0) = x (t0)+iy (t0) направлен по касательной к кривой Г в точке z0.
Пусть w0 = f(z0) - образ точки z0, а L - образ кривой Г при отображении w = f (z) плоскости XOY на плоскость UOV (рис. 1.12). Уравнение кривой L имеет
Рис. 1.12
вид w = w(t) = f[z(t)]. По правилу дифференцирования сложной функ-
ции w (t) = f |
[z(t)]z (t). |
|
|
|
|
Так как f (z0) |
0, z (t0) 0, то w |
(t0) = f (z0)z (t0) 0. |
|
|
|
Следовательно, |
|
|
|
||
|
|
Argw (t0) = argf |
(z0)+Argz (t0) = |
+Argz (t0), |
(1.49) |
где |
= arg f |
(z0) не зависит от вида кривой Г. |
Векторы z |
(t0) |
|
и w |
(t0) определяют направление касательной к кривым Г и L соот- |
||||
ветственно в точках z0 и w0 . Поэтому равенство (1.49) позволяет сделать следующий вывод.
Если аналитическая функция f (z) имеет в точке z0 произ-
водную f  (z0) 0, то аргумент этой производной равен углу, на который нужно повернуть касательную в точке z0 к любой кри-
(z0) 0, то аргумент этой производной равен углу, на который нужно повернуть касательную в точке z0 к любой кри-
38
вой, проходящей через эту точку, чтобы получить направление касательной в соответствующей точке w0 к образу данной кривой при отображении w = f (z) . Если = arg f  (z0)>0, то поворот происходит
(z0)>0, то поворот происходит
против часовой стрелки, если |
< 0, то по часовой стрелке. |
Если через точку z0 |
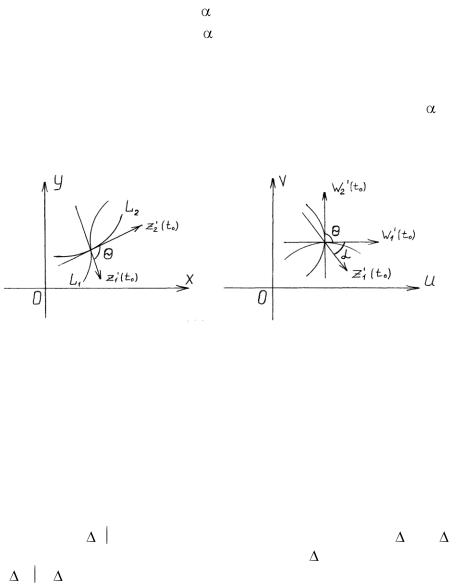
провести любые две кривые Г1 и Г2, |
имеющие касательные в этой точке, то направление касательных к
образам L1 и L2 этих кривых в точке |
w0 = f(z0) получаются путем |
|
поворота касательных к кривым Г1 |
и Г2 на один и тот же угол . По- |
|
этому угол между кривыми L1 и L2 |
по величине и направлению сов- |
|
падает с углом между кривыми Г1 и Г2 |
(рис. 1.13). |
|
. |
Рис.1.13 |
Отображение, сохраняющее углы между линиями, называется конформным. Если при этом сохраняется и на-правление отсчета углов, то такое отображение называется конформным отображением первого рода.
Таким образом, отображение, осуществляемое аналитической функцией, является конформным отображением первого рода во всех точках, в которых производная от этой функции отлична от нуля.
Чтобы выяснить геометрический смысл модуля производной, заметим, что 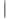 z равен расстоянию между точками z0 и z0+ z, а
z равен расстоянию между точками z0 и z0+ z, а 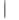 w
w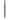 равен расстоянию между точками w0 и w0+ w. Поэтому величина
равен расстоянию между точками w0 и w0+ w. Поэтому величина
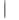 w /
w / z
z показывает, в каком отношении изменяется расстояние
показывает, в каком отношении изменяется расстояние
39
