
Методическое пособие 582
.pdf
|
1 |
i |
|
|
f (t) = |
F ( p)e pt dp . |
(2.31) |
||
2 i |
||||
|
i |
|
Интеграл в правой части этого равенства, так же как интеграл в формулах прямого и обратного преобразования Фурье, понимается в смысле главного значения. Это означает, что
|
i |
ib |
|
|
|
F ( p)e pt dp = lim F ( p)e pt dp . |
|
|
|
|
|
b |
|
|
|
i |
ib |
|
|
|
Функция f (t) , определяемая по формуле (2.31), называется |
|||
|
обратным преобразованием Лапласа для функции F(p). |
|
||
|
Предыдущие рассуждения являются нестрогим дока- |
|||
|
зательством следующей теоремы. |
|
|
|
|
Теорема. Если функция F( p) комплексного переменного |
|||
p |
i аналитична в некоторой полуплости Re p |
0 |
и |
|
|
|
|
|
|
удовлетворяет условию |
lim F( p) =0, |
|
|
|
|
|
p |
|
|
то функция F( p) является преобразованием Лапласа для функции f (t) , причем
|
1 |
i |
|
f (t) = |
F ( p)e pt dp при t > 0, и f (t) = 0 при t < 0. |
||
2 i |
|||
|
i |
||
|
|
Непосредственное вычисление интеграла, стоящего в правой части формулы (2.31) очень часто сопряжено с большими трудностями. Рассмотрим случаи, когда обратное преобразование Лапласа можно найти более простыми способами.
2.3.1. Применение вычетов для отыскания обратного преобразования Лапласа
На практике очень часто изображение Лапласа аналитично не только в полуплоскости Re p 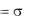
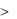 0 , но и во всей плоскости
0 , но и во всей плоскости
комплексного переменного p, кроме конечного числа особых точек. В этом случае справедлива следующая теорема:
100

Теорема. Если функция F( p) аналитична в плоскости комплексного переменного p кроме конечного числа особых точек
p1, p2,..., pn, и если lim F( p) =0, то функция F( p) является пре- |
||||||||||
|
|
p |
|
|
|
|
|
|
|
|
образованием Лапласа для функции f (t) , причем |
|
|
||||||||
n |
|
|
|
|
|
|
|
|
|
|
f (t) = |
Re s[F ( p)e pt , pk ] |
при t > 0 и |
f (t) = 0 при t < 0. |
|||||||
k |
1 |
|
|
|
|
|
|
|
|
|
Для доказательства теоремы построим на плоскости ком- |
||||||||||
плексного переменного p замкну- |
|
|
|
|
|
|||||
тый контур C, состоящий из отрез- |
|
|
|
|
|
|||||
ка AB прямой Re p |
|
0 |
и ду- |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
ги CR радиуса R с центром в нача- |
|
|
|
|
|
|||||
ле координат (рис. 2.9). Отрезок AB |
|
|
|
|
|
|||||
и радиус R дуги CR |
выберем так, |
|
|
|
|
|
||||
чтобы все особые точки |
p1, p2, ..., pn |
|
|
|
|
|
||||
функции F( p) лежали внутри об- |
|
|
|
|
|
|||||
ласти, ограниченной контуром С. |
|
|
Рис. 2.9 |
|
|
|||||
Тогда, в силу основной теоремы о вычетах |
|
|
||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
F ( p)e pt dp = |
2 i |
Re s[F ( p)e pt , p |
k |
] , или |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
F ( p)e pt dp + |
F ( p)e pt dp = 2 i |
Re s[F ( p)e pt , p |
k |
] . |
||||||
|
|
|
|
|
|
|
|
|
|
|
AB |
|
CR |
|
|
k 1 |
|
|
|
|
|
В силу леммы Жордана (см. 1.18.3) при t > 0 |
|
|
|
|||||||
|
|
lim |
|
F ( p)e pt dp = 0. |
|
|
|
|
|
|
|
|
R |
CR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
Так как lim |
F ( p)e pt dp = |
F ( p)e pt dp , то |
|
|
|
|
||||
R |
|
|
|
|
i |
|
|
|
|
|
AB |
|
|
|
|
|
|
|
|
||
101

|
1 |
i |
|
1 |
|
|
|
|
|
|
|
|
|
f (t) = |
|
|
F ( p)e pt dp = |
|
lim ( |
F ( p)e pt dp + |
2 i |
|
|
||||
|
2 i |
|||||
|
i |
|
R |
AB |
||
|
|
|
|
|
n
+F ( p)e pt dp )= Re s[F ( p)e pt , pk ] .
CR |
k 1 |
Так же можно доказать, что при t < 0 f (t) = 0.
2.3.2. Оригиналы рациональных изображений
Рассмотрим случай, когда изображение F( p) является правильной дробно-рациональной функцией переменного p:
F( p) |
A( p) |
, |
(2.32) |
|
B( p) |
||||
|
|
|
где A(p) и B(p) многочлены, причем степень числителя меньше степени знаменателя.
Как известно из анализа, функцию (2.32) можно представить в виде суммы простейших дробно-рациональных функций,
то есть в виде суммы дробей вида
|
M |
|
, |
|
M |
, |
Mp |
N |
|
, |
|
|
Mp |
N |
|
, |
(2.33) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
p |
a |
( p |
a)k |
p2 |
ap |
b |
( p2 ap b)k |
|||||||||||
где 4b a2 |
0 . Оригиналы функций (2.33) находятся с помощью |
||||||||||||||||||
формул (2.3), (2.4), (2.6) - (2.9), (2,12) - (2.15), (2,22). |
|
|
|||||||||||||||||
|
|
|
|
M |
|
Meat , |
|
M |
|
|
Mt k |
1eat |
, |
|
|
||||
|
|
|
|
p |
a |
( p |
a)k |
|
(k |
1)! |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
102
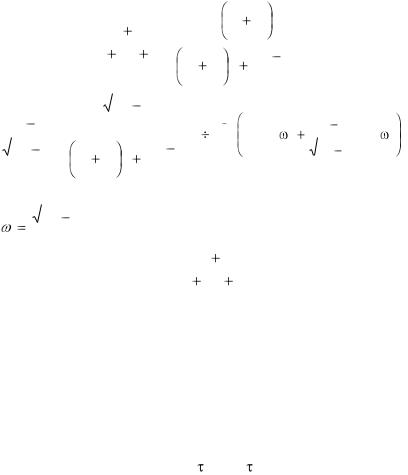
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
p |
|
|
a |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Mp |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
2 |
|
|
+ |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
p2 |
ap b |
p |
|
|
a 2 |
|
|
4b a 2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4b |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
N Ma |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
at |
|
|
|
|
|
|
|
|
2 |
N Ma |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin t , |
|||||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e 2 |
|
M cos t |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a 2 |
4b a2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
4b a2 |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4b a2 |
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
4b |
a 2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Оригинал дроби вида |
|
|
Mp |
N |
|
|
|
|
проще всего находится |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
( p2 |
|
ap |
|
|
b)k |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
с помощью вычетов. Оригиналы рациональных изображений находятся как суммы оригиналов простейших дробнорациональных функций.
2.4 Теорема об умножении изображений. Интеграл Дюамеля
Пусть функции f (t) и g(t) являются оригиналами. Функция
t
h(t) = 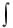 f ( )g(t
f ( )g(t  )d
)d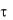
0
называется сверткой оригиналов и обозначается h(t) = f (t) * g(t) .
Операция свертывания оригиналов обладает свойствами коммутативности и ассоциативности:
1.g(t) * f (t) = f (t) * g(t) ,
2.h(t) *[ f (t) * g(t) ] = [ h(t) * f (t) ]* g(t) .
103
Проверим, например, свойство коммутативности. Имеем
t
g(t) * f (t) = g( ) f (t 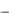 )d .
)d .
0
Сделаем в этом интеграле замену переменной
t 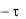
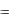 1, d
1, d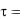 d 1 .
d 1 .
Получим
t |
0 |
g(t) * f (t) = g( ) f (t |
)d =- g(t 1 ) f ( 1 )d 1 = |
0 |
t |
t |
|
=  f (τ1 )g(t τ1 )d 1 = f (t) * g(t) .
f (τ1 )g(t τ1 )d 1 = f (t) * g(t) .
0
Свойства коммутативности и ассоциативности поз-воляют находить свертку трех и более оригиналов, причем порядок свер-
тываемых функций не играет роли. Легко проверяется, что свертка оригиналов также является оригиналом.
Теорема 1. Если f (t) |
F( p) , g(t) |
G( p) , то |
|
f (t) * g(t) |
F( p) G( p) , |
||
при свертывании оригиналов их изображения перемножаются. Доказательство. Пусть
|
t |
|
h(t) = f (t) * g(t) = f ( )g(t |
)d . |
|
|
0 |
|
Тогда |
|
|
|
t |
|
H ( p) = e pr dt f ( )g(t |
)d . |
|
0 |
0 |
|
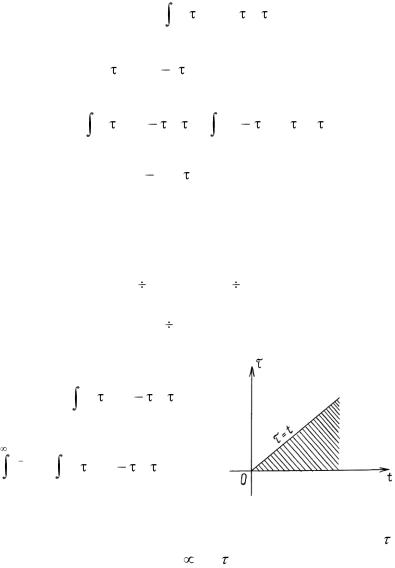
Рис.2.10
Интеграл в правой части этого равенства является повторным интегралом по неограниченной области D в плоскости (t, ), определяемой неравенствами 0<t< , 0< <t (рис. 2.10).
Если в повторном интеграле изменить порядок интегрирования, то получим
104

|
t |
|
H ( p) = e pt dt f ( )g(t |
)d = f ( )d g(t )e pt dt . |
|
0 |
0 |
0 |
Во внутреннем интеграле правой части сделаем замену перемен-
ной t - =t1, t =t1 + |
, dt = dt1. В результате получим |
|
|
|||
|
H ( p) = |
f ( )d g(t1 )e |
p(t1 ) |
dt1 = f ( )e |
p |
d |
|
|
|
||||
|
0 |
0 |
|
0 |
|
|
g(t )e pt1 dt = |
F( p) G( p) , что и требовалось доказать. |
|||||
1 |
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
Теорема 1 называется теоремой об умножении изображений. Аналогично доказывается теорема об умножении ори-
гиналов.
Теорема 2. Если f (t) и g(t) - оригиналы, порядок роста
которых соответственно равен |
1 и 2, и если |
|||||
|
|
|
f (t) |
F( p) , g(t) G( p) , то |
||
|
1 |
a i |
|
|
||
f (t) g(t) |
F(q)G( p |
q)dq , где a > 1, Rep= > a + 2. |
||||
|
|
|||||
|
2 i |
|||||
|
|
a i |
|
|
||
|
a i |
|
|
|
||
Интеграл |
|
F(q)G( p q)dq называется сверткой изображений. |
||||
a i
Таким образом, умножению изображений соответствует свертывание оригиналов, умножению оригиналов соответствует свертывание изображений и деление результата на 2 i.
Пользуясь теоремой 1, найдем оригинал для изображений вида p F( p) G( p) , где F( p) 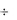 f (t) , G( p)
f (t) , G( p) 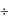 g(t) .
g(t) .
Для этого заметим, что
p F( p) G( p) =[ p F( p) - f (0) ] G( p) + f (0) G( p) ,
или
p F( p) G( p) =[ p G( p) - g(0) ] F( p) + g(0) F( p) .
Отсюда следует, что
p F( p) G( p) 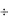 f ' (t) * g(t) + f (0) g(t) ,
f ' (t) * g(t) + f (0) g(t) ,
105
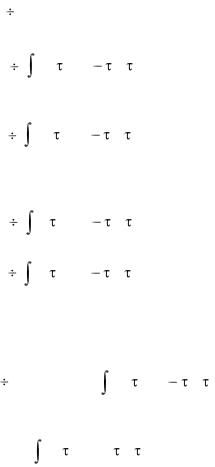
или |
|
|
|
|
p F( p) G( p) |
g' (t) * f (t) |
+ g(0) f (t) , |
|
|
то есть |
|
|
|
|
|
t |
|
|
|
p F( p) G( p) |
f ' ( )g(t |
)d |
+ f (0) g(t) , |
(2.34) |
|
0 |
|
|
|
или |
|
|
|
|
|
t |
|
|
|
p F( p) G( p) |
g' ( ) f (t |
)d |
+ g(0) f (t) . |
(2.35) |
0
Если воспользоваться коммутативностью свертки, то соотношения (2.34) и (2.35) принимают вид
|
t |
|
|
|
p F( p) G( p) |
g( ) f ' (t |
)d |
+ f (0) g(t) , |
(2.36) |
|
0 |
|
|
|
|
t |
|
|
|
p F( p) G( p) |
f ( )g' (t |
)d |
+ g(0) f (t) . |
(2.37) |
|
0 |
|
|
|
Интеграл в правых частях соотношений (2.34)-(2.37) на-
зывается интегралом Дюамеля. В частности, если |
f (0) = 0, |
t |
|
то p F( p) G( p) f ' (t) * g(t) = f ' ( )g(t |
)d , |
0
а если g(0) = 0,
t
то F( p) G( p) 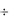 g' (t) * f (t) = g' ( ) f (t
g' (t) * f (t) = g' ( ) f (t  )d .
)d .
0
2.5. Теоремы о разложении
Для отыскания прямого и обратного преобразования Лапласа очень часто используются следующие две теоремы, которые
приводятся здесь без доказательства.
106

Теорема 1. Если функция F( p) аналитична в области
p >R, удовлетворяет условию lim F( p) = 0 и разлагается в
p
ряд Лорана F( p) = |
ck |
, то функция F( p) является изображе- |
||
|
||||
k 1 |
pk |
|||
|
нием для функции |
|||
|
|
|
ck t k 1 |
|
|
f (t) = k 1 |
|
. |
|
|
(k 1)! |
|||
Теорема 2. Если функция f (t) , рассматриваемая как функ-
ция комплексного переменного t, аналитична на всей комплексной плоскости, имеет конечный порядок роста при
t + и разлагается в степенной ряд
|
|
|
|
|
|
|
|
|
|
f (t) = |
|
|
ck t k |
, |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
||||||
то изображение F( p) |
функции |
|
f (t) |
разлагается в |
ряд вида |
|||||||||||||||||||||||
|
ck k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
F( p) = k 0 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pk 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1. Показать, что функция F( p) |
= |
|
|
|
1 |
|
является изобра- |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
p2 1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
жением функции Бесселя |
J 0 (t) = |
|
( |
1)k t2k |
|
. |
|
|
|
|
|
|
|
|||||||||||||||
0 2 |
2k (k!)2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|||||||
Для решения этой задачи разложим функцию |
|
1 |
|
|
в ряд |
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
p2 |
1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Лорана по степеням |
1 |
|
. Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
1/ 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
p2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
p2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
107

|
1 |
|
1 |
|
|
( |
|
1/ 2)( |
3 / 2)...( |
(2k |
|
1) / 2) |
|
1 |
. |
|
|
|||||||||||||||||||||||||||||
|
|
|
p |
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
p2k |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Так как 1 3 5 ... (2k-1) = |
(2k)! |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2k k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
= |
|
|
|
|
|
( 1)k (2k )! |
|
|
|
|
|
|
( 1)k t 2k |
|
J |
0 (t) . |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2k |
(k!) |
2 |
|
p |
2k 1 |
|
|
|
k 0 2 |
2k |
(k!) |
2 |
|
|
|
||||||||||||||||||
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
1 k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
2. Разложить в степенной ряд функцию |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
et |
|
|
e |
t |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
f (t) = |
|
cht cost = |
|
|
|
|
|
|
|
|
|
cost . |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
По теореме о смещении изображения находим, что |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
F(p)= |
|
1 |
|
|
|
|
|
p |
1 |
|
|
|
|
|
|
|
|
|
p |
1 |
|
|
|
|
|
= |
|
|
p3 |
|
|
. |
|
|
||||||||||
|
|
|
2 ( p 1)2 |
1 ( p 1)2 |
|
1 |
|
p4 |
4 |
|
|
|||||||||||||||||||||||||||||||||||
Разложим функцию |
|
|
p |
3 |
|
|
в степенной ряд по степеням |
1 |
в |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
p4 |
4 |
|
p |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
области p > 2. Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
F(p) = |
|
|
p3 |
|
= = |
|
1 |
|
|
1 |
|
|
= |
|
|
|
|
|
( 1)k 4k |
|
. |
|
|
||||||||||||||||||||
|
|
|
p4 |
|
4 |
|
p |
1 |
|
4 |
|
|
|
k |
0 |
p4k 1 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p4 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
f (t) = cht cost |
= |
( |
1)k 4k t 4k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
(4k )! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.6.Применения преобразования Лапласа
2.6.1.Решение задачи Коши для линейных дифференциальных уравнений и систем с постоянными коэффициентами.
Применение интеграла Дюамеля
108

Пусть требуется найти частное решение дифференциального уравнения
a |
0 |
x(n) |
a x(n 1) |
.... a |
n 1 |
x' |
a |
n |
x |
|
f (t) , |
(2.38) |
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
удовлетворяющее начальным условиям |
|
|
|
|
|
|
|
|||||||
|
|
x(0) |
x |
, x' (0) |
x ,...., x(n 1) |
|
x |
n 1 |
. |
(2.39) |
||||
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
Будем предполагать, что решение x(t) и его производные |
||||||||||||||
x' (t), x"(t), ... , x(n-1)(t), а также функция |
f (t) |
являются оригина- |
||||||||||||
лами. Тогда, применяя преобразование Лапласа к левой и правой частям уравнения (2.38), получим
|
|
a |
[ pn X ( p) |
pn 1 x |
0 |
pn 2 x |
.... |
x |
n 1 |
] + |
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
+ a [ pn 1 X ( p) |
|
pn 2 x |
0 |
pn 3 x |
|
|
|
... x |
n 2 |
] + |
+ a |
n |
X ( p) |
F ( p) |
|||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A( p)X ( p) |
B( p) |
F( p) , |
|
|
|
(2.40) |
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A( p) a |
0 |
pn |
a pn 1 |
..... a |
n |
– |
характеристический |
многочлен |
|||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнения (2.38), B( p) |
- многочлен, степень которого не превы- |
||||||||||||||||||
шает n-1, зависящий от начальных условий x0, x1, ..., xn-1. |
|||||||||||||||||||
Из уравнения (2.40) находим, что |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
X ( p) |
|
|
B( p) F( p) |
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
A( p) |
|
|
|
|
|
|
|
|
Отсюда с помощью обратного преобразования Лапласа находится искомое решение x(t).
Пример. Найти решение задачи Коши
x" a2 x b sin at, x(0) x |
0 |
, x' (0) |
x . |
|
|
1 |
Применяя преобразование Лапласа, получим
p2 X ( p) px x a2 X ( p) |
|
ab |
|
. |
|
|
|
||
p2 |
|
a2 |
||
0 1 |
|
|
Отсюда следует, что
109
