Методическое пособие 498

Рассмотрим наиболее типичные базисы.

Разложение Карунена-Лоэва

Пусть система функций k t определяется как решение интегрального уравнения вида

Тогда случайные числа k в (5.22) будут не коррелированны между собой, т.е.

k l k kl ,

причем 0 1 2 . Некоррелированность коэффициентов

k прямо следует из уравнения (6.8).

Ортогональное разложение (5.22), (6.8), называемое в литературе разложением Карунена-Лоэва, является наиболее быстро сходящимся из всех имеющихся. При этом алгоритм формирования случайных процессов на основе (5.22), (6.8) обладает весьма высоким быстродействием, так как функцииk t могут быть вычислены до моделирования.

Основным недостатком разложения Карунена-Лоэва является необходимость решения интегрального уравнения (6.8). Однако если аналитически явный вид функций k t

получить не удается, то (6.8) может быть решено численно, а функции k t – заданы с помощью массивов.

Пример 6.3. Получить разложение Карунена-Лоэва для

111

сводится к эквивалентному дифференциальному уравнению вида

Имеется два фундаментальных решения дифференциального уравнения (6.10):

Тогда собственные функции и собственные значения имеют вид

k t 2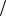T sin k 0,5 tT , k T2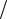 2 k 0,5 2 .

Приведение интегрального уравнения (6.9) к дифференциальному уравнению несложно для процессов с дробно-рациональной спектральной плотностью (6.6). Далее дифференциальное уравнение высокого (четного) порядка сводится к системе уравнений второго порядка, и ищется набор

112

собственных функций и собственных значений в векторноматричной форме. Однако эта технология достаточно громоздка и редко используется. Процессы со спектральной плотностью вида (6.6) достаточно эффективно моделируются рекуррентным алгоритмом. Для других видов спектров и корреляционных функций необходимо иметь или аналитическое или численное решение уравнения Фредгольма

(6.8).

Разложение в ряд Фурье

Случайный процесс x t длительностью TM может быть представлен в виде ряда

Из (6.11) следует, что реализации x t периодически повторяются через интервал времени T.

Определим параметры разложения (6.11) с целью формирования процесса с заданной корреляционной функцией R . Согласно (6.11)

113

Здесь G – спектральная плотность процесса x t . Таким образом, при выполнении (6.15) для дисперсий случайных величин Uk , Vk (2.47) имеем

при TM кор ряд (6.11) оказывается медленно сходящимся, так

что число слагаемых в нем оказывается достаточно большим. В этой связи алгоритм (6.11) получил распространение лишь для формирования коротких отрезков (реализаций) случайных процессов. В общем случае число слагаемых ряда (6.11) можно оценить из соотношений

114

слагаемых в (6.11) не превышает 200. Если сравнить данный метод с методом скользящего суммирования, в котором число весовых коэффициентов достигает 1000-2000 (см. табл. 2.2) для формирования одного отсчета реализации x t , то для данного набора параметров алгоритм имитации (6.11) оказывается вполне приемлемым.

Пример 6.6. Сформировать случайный процесс с характеристиками

R exp 2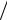2 кор2 , G кор 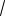2 exp 2 кор2 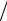2 .

скользящего суммирования. Для формирования более длинных реализаций процесса x t алгоритм скользящего суммирования является основным способом статистического моделирования.

Цифровым аналогом (2.47) является дискретное преобразование Фурье процесса x t , определяемое как [9]

Здесь N TM 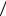t , t – шаг дискретизации. Число слагаемых в сумме (6.17) должно быть не меньше, чем число слагаемых kmax непрерывного ряда (6.11). Отсюда возникают

дополнительные ограничения на шаг дискретизации t . Однако, в отличие от (6.11) алгоритм (6.17) может быть реализован при помощи быстрого преобразования Фурье, что повышает его быстродействие по сравнению с (6.11).

115

является возможность формирования процесса x t в любой заданной точке и по любой, даже неравномерной сетке отсчетов. Недостатком метода является ограничение на длину реализации.

6.3. Неканонические разложения

Метод неканонических разложений основывается на представлении случайного процесса в виде неслучайной функции со случайными параметрами. Одно из возможных представлений имеет вид

процесс (6.20) является стационарным, но неэргодическим [10]. Перепишем (6.20) в виде

(комплексная амплитуда). Если A описывается распределением Релея, φ – равномерно распределенная случайная величина, то

Здесь A2 – дисперсия амплитуды A,

t2 t1 w exp j t2 t1 d

– характеристическая функция случайной величины ω. Процесс (6.21), (6.22) является стационарным в

широком смысле. При этом для его выборочной корреляционной функции имеем:

117

1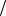2 Re A2 exp j .

Как видно из (6.23), выборочная корреляционная функция остается функцией случайных величин A, и никак не сходится к истинной корреляционной функции R (6.22).

Иногда предлагают использовать обобщение (6.20) в

N

виде суммы процессов x t C Ai cos it i . Однако

i 1

условие эргодичности здесь также не выполняется.

6.4. Контрольные вопросы

1.Перечислите основные этапы формирования отсчетов случайного процесса на ЭВМ рекуррентным методом.

2.Для формирования каких случайных процессов рекуррентный метод является эффективным и практически реализуемым?

3.Каким образом могут быть заданы начальные условия при формировании на ЭВМ случайного процесса рекуррентным методом?

4.Назовите достоинства и недостатки рекуррентного метода моделирования случайных процессов.

5.Какие базисы функций целесообразно использовать при моделировании случайных процессов методом канонических разложений?

6.Как осуществляется представление случайного процесса в базисе Карунена-Лоэва? Каковы преимущества и недостатки этого базиса?

7.Как осуществляется разложение случайного процесса

вряд Фурье? Каким образом выбираются параметры разложения? Укажите особенности использования дискретного преобразования Фурье.

8.Перечислите достоинства и недостатки метода

118

ортогональных разложений для формирования реализаций случайных процессов.

9. В чем суть метода неканонических разложений для формирования случайного процесса с заданными характеристиками?

6.5. Задачи

1.Сформировать гауссовский процесс со спектральной плотностью G G0 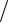1 2 2 .

2.Сформировать гауссовский процесс с корреляционной функцией R exp 1 2 2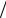3 .

3.Сформировать гауссовский процесс с корреляционной

функция.

4.Сформировать случайный процесс с корреляционной функцией K 12 exp 1 cos 1 22 exp 2 cos 2 ,

1 2 , 1 2 .

5.Методом ортогональных разложений сформировать

стандартный винеровский случайный процесс.

6. Методом ортогональных разложений сформировать случайный процесс со спектральной плотностью фон Кармана

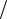G G0 L2 2 116 exp 2 m2 ,

где L 2 L0 , m 5,92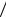l0 , l0 0,1, L0 1000.

7. Методом разложения в ряд Фурье сформировать случайный процесс с корреляционной функцией R exp на интервале TM 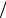кор 30.

8.Методом разложения в ряд Фурье сформировать процесс с корреляционной функцией R exp 2 cos 2 .

9.Методом неканонических разложений сформировать

случайный процесс с корреляционной функцией

R exp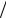 22 .

119

7. МОДЕЛИРОВАНИЕ КВАЗИГАРМОНИЧЕСКИХ И НЕГАУССОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ

7.1. Моделирование квазигармонических и типовых негауссовских случайных процессов

7.1.1. Моделирование квазигармонических случайных процессов на ЭВМ

Квазигармоническим процессом называется случайный процесс вида

Корреляционная функция квазигармонического процесса отражает характер его изменения во времени и в общем случае может быть записана как

R cos 0 Rc cos 0 Rs sin 0 .

Здесь , – некоторые медленно меняющиеся функции

(огибающая и фаза),

Rc cos , Rs sin .

120