
Методическое пособие 498
.pdf
Здесь R j m R j m t .
Системная функция H z формирующего фильтра равна
L
H z ak z k
k 0
|
M |
|
(5.21) |
1 bmz m . |
|||
|
m 1 |
|
|
Делая в (5.21) подстановку z exp j t , можно записать
Gx G0 H exp j t 2 .
Метод ортогональных (канонических) разложений
основан на разложении процесса в ряд по некоторой системе функций k t :
|
|
|
x t k k t , |
t T , |
(5.22) |
k
где коэффициенты k – гауссовские случайные числа. Для практических целей систему базисных функций k t удобно выбирать ортогональной, а коэффициенты k –
некоррелированными. Такой способ весьма прост и особенно эффективен при моделировании случайных полей. Также с его помощью можно легко моделировать нестационарные процессы.
При практической реализации в ряде (5.22) используют конечное число членов N, определяемое требуемой погрешностью аппроксимации. Если T кор , где кор – время
корреляции процесса x t , то число значащих членов N в (5.22)
сравнительно невелико. Однако при T кор ряд (5.22)
оказывается медленно сходящимся, так что число слагаемых в нем оказывается достаточно большим. В этой связи алгоритм (5.22) получил распространение лишь для формирования коротких отрезков (реализаций) случайных процессов. Вариантами этого метода являются разложение КаруненаЛоэва, каноническое разложение Пугачева, разложение в ряд Фурье (в том числе дискретное преобразование Фурье).
91

Метод коррелированных векторов состоит в
преобразовании |
|
|
вектора-столбца |
некоррелированных |
||
случайных чисел |
|
U u1,u2, ,uN T |
в |
вектор-столбец |
||
X x1,x2, ,xN T |
|
коррелированных отсчетов посредством |
||||
матричного преобразования |
|
|
||||
Здесь xj x j , |
|
|
|
X AU. |
|
(5.23) |
j |
|
, N – число отсчетов, |
а индекс «T» |
|||
1,N |
||||||
обозначает операцию транспонирования. Матрица A является треугольной
|
a |
0 |
0 |
|
0 |
|
|
|
|
11 |
a22 |
0 |
|
0 |
|
A |
a21 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||
|
|
|
aN2 |
aN3 |
|
|
|
|
aN1 |
aNN |
|||||
и получается с помощью разложения Холецкого корреляционной матрицы R вектора X:
|
R |
R |
|
R |
|
|
|
|
|
11 |
12 |
|
1N |
|
|
|
|
R21 |
R22 |
|
R1N |
AA |
T |
|
T |
|
R |
|
|
|
|
|
X X , (5.24) |
||
RN1 2RN RNN
где AT – транспонированная матрица, которая может быть найдена с помощью следующего итерационного алгоритма:
a11 R11 , |
ak1 Rk1 a11 , |
|
k 2, ,N , |
||||
|
|
|
n 1 |
|
|
|
|
akn |
|
|
|
|
ann , |
n 2, ,k 1, |
|
Rkn |
akjanj |
||||||
|
|
|
j 0 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
ann |
Rnn anj2 . |
|||
|
|
|
|
|
j 1 |
|
|
Моделирование процессов с помощью указанного алгоритма целесообразно для формирования коротких реализаций нестационарных случайных процессов. Обычно
92

этот алгоритм применяется для формирования начальных точек в рекуррентном методе для ликвидации переходного процесса.
Метод условных распределений по своей идее относится к самым общим методам формирования реализаций случайных процессов. Предположим, что нам необходимо получить вектор отсчетов X x1,x2, ,xN процесса x t с заданной многомерной плотностью вероятности
w x1,x2, ,xN w x1 w x2 x1 w x3 x1,x2 w xN x1,x2, ,xN 1 .
Из этого выражения следует, что сначала формируется случайное число x1 с распределением w x1 , затем на основе метода суперпозиции число x2 с распределением w x2 x1 и так
далее. Применение этого метода целесообразно только в случае получения коротких реализаций, у которых распределение вероятностей отсчетов xj меняется. Например, данный
алгоритм может использоваться для формирования произвольных марковских случайных процессов, заданных распределением
w x1,x2, ,xN w x1 w x2 x1 w x3 x2 w xN xN 1 .
Блок-схема моделирования марковского процесса приведена на рис. 5.3.
Если же класс марковских процессов сужается до процессов гауссовского типа, то более эффективным является метод формирующего фильтра.
Рис. 5.3
93
5.4. Метод скользящего суммирования
Формирование реализаций дискретного гауссовского случайного процесса x j с нулевым матожиданием и единичной дисперсией по методу скользящего суммирования осуществляется в соответствии с (5.18) согласно алгоритму
|
|
x j ck j k . |
(5.25) |
k
Здесь – независимые гауссовские величины с параметрами
~ N 0,1 , ck – весовые коэффициенты. |
При этом должно |
||
выполняться условие |
|
|
|
x2 j |
|
|
|
ck2 |
1. |
(5.26) |
|
k
Весовые коэффициенты ck в (5.25) можно рассчитать по нескольким методикам.
Метод инвариантной импульсной характеристики формирующего фильтра. Обозначим h h0g , где h0 –
некоторая размерная константа в импульсной характеристике аналогового формирующего фильтра (5.16). Если удается в явном виде получить соответствие между корреляционной функцией R формируемого процесса и функцией g , то
коэффициенты ck могут быть найдены как |
|
ck b g k t , |
(5.27) |
Константа b в (5.27) аналитически или численно доопределяется из соотношения
|
|
b2 g2 k t 1. |
(5.28) |
k
Отметим, что при нахождении суммы ряда (5.28) может использоваться интегральная оценка (см. пример 5.2).
Пример 5.3. Рассчитать весовые коэффициенты для
94

моделирования процесса x t на выходе интегрирующей цепи.
|
Решение. |
Для интегрирующей цепи h t h0 exp t , |
||||||||||||||
t 0. |
Обозначим: |
t k t, |
t , |
тогда |
ck bexp k , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0. |
Из условия |
ck2 |
1 |
получаем |
b |
|
, |
или, |
||||||||
1 exp 2 |
||||||||||||||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
при 1, b |
|
. В результате |
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
ck |
|
|
|
|
|
exp k , |
|
(5.29) |
||||
|
|
|
|
|
|
2 |
|
|||||||||
и, соответственно, коэффициент корреляции |
процесса |
x t |
||||||||||||||
определится как R exp |
|
|
|
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
|
Корреляционные |
функции |
некоторых |
типовых |
||||||||||||
случайных процессов, соответствующие им спектральные плотности, импульсные характеристики аналогового фильтра и весовые коэффициенты формирующего цифрового фильтра приведены в табл. 5.1. Здесь t , – целая часть числа.
Более подробные таблицы коэффициентов ck для различных
случайных процессов можно найти в [11].
Пример 5.4. Рассчитать цифровой формирующий фильтр для моделирования процесса с корреляционной функцией R exp 2 2 2 .
2 .
Решение. Согласно табл. 5.1 для заданной корреляционной функции g exp 2 2 . Тогда
c bexp k2 2 t2 bexp k2 2 . |
|
|
||
k |
|
|
|
|
Из (5.28) для множителя b имеем |
|
|
||
|
|
|
|
|
|
b2 exp 2k2 2 1. |
|
(5.30) |
|
|
k |
|
|
|
Воспользуемся интегральной оценкой суммы ряда (5.30): |
|
|||
|
|
|
|
|
b2 exp 2k2 2 b2 exp 2 2x2 dx b2 |
2 2 |
1. |
||
k |
|
|
|
|
|
|
|
||
Тогда b 4 |
2 2 , и мы получаем соответствующее |
|||
выражение для ck |
из табл. 5.1. |
|
|
|
95
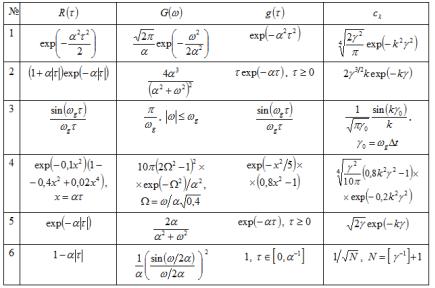
Таблица 5.1
Особенности метода инвариантных импульсных характеристик:
1)метод является универсальным и позволяет формировать процессы с любыми спектральнокорреляционными характеристиками.;
2)корреляционные функции непрерывного и дискретного процессов совпадают;
3)спектральные плотности непрерывного и дискретного процессов в общем случае отличаются, однако при t 0 эти отличия малы;
4)необходимо знание непрерывного аналога формирующего фильтра.
Метод обратного дискретного преобразования Фурье.
Если импульсная характеристика формирующего фильтра неизвестна, но задан вид спектральной плотности
Gx (или корреляционной функции) моделируемого процесса x t , то для расчета весовых коэффициентов может быть использован метод преобразования Фурье.
96
Как известно [10], пара преобразований Фурье для
непрерывного процесса |
f t имеет вид |
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
||||
F f t exp j t dt, |
f t |
F exp j t d , |
|||||||||||
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||
а дискретизированного - |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fg f n t exp j n t , |
|
|
|||||||||||
n |
|
|
|
|
|
|
|
|
|
|
(5.31) |
||
|
t |
t |
|
|
|
|
|
|
|
|
|||
f n t |
Fg exp j n t d . |
|
|||||||||||
2 |
|
||||||||||||
|
t |
|
|
|
|
|
|
|
|
|
|||
Спектры непрерывного |
|
и |
дискретизированного |
||||||||||
процессов связаны соотношением |
|
|
|
2m |
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|||||
Fg |
|
F |
|
|
|
|
, |
(5.32) |
|||||
|
|
|
|||||||||||
|
|
|
t m |
|
|
|
|
t |
|
|
|||
т.е. спектр дискретизированного процесса получается путем периодического продолжения спектра непрерывного сигнала. В связи с этим спектр Gx непрерывного процесса x t должен
быть ограничен полосой частот g . При неограниченном по частоте спектре Gx для возможности представления x t
в цифровой форме необходимо выполнить операцию усечения вида
~ |
G |
, |
|
|
, |
|
||||
|
x |
|
|
|
|
|
g |
|
|
|
Gx |
|
|
|
|
|
|
|
|
|
(5.33) |
0, |
|
|
|
|
|
|||||
|
|
|
||||||||
|
|
|
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
||
где g t . Граничная |
частота спектра g (шаг |
|||||||||
дискретизации t ) в (5.33) выбирается, исходя из допустимых искажений спектра формируемого процесса.
Основываясь на (5.31), (5.32), можно записать спектральную плотность Gg дискретного процесса x j в
полосе частот g как Gg Gx  t.
t.
Из (5.15) следует, что передаточная функция Hg j
дискретного формирующего фильтра связана со спектральной
97
плотностью Gg дискретного процесса x j соотношением
Gg Hg j 2 .
Тогда, поскольку при цифровом статистическом моделировании отсутствуют проблемы физической реализуемости фильтра, можно считать, что формирующий фильтр имеет действительную передаточную функцию
Hg 
 Gg
Gg 
 Gx
Gx 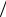 t .
t .
В результате согласно (5.31) импульсная характеристика цифрового формирующего фильтра имеет вид
|
|
t |
t |
|
|
|
|
|
|
t |
t |
||||||
ck |
|
|
|
Hg exp j k t d |
|
|
|
|
|
|
|||||||
2 |
|
|
|
||||||||||||||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
0 |
||
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
g |
|
|
|
|
1 |
||||||||
|
|
|
|
Gx |
|
|
k |
|
|
|
|
||||||
|
|
|
|
cos |
d |
|
|
|
|
||||||||
|
g 0 |
|
|
|
g |
|
|
|
g 0 |
||||||||
1
t Gx cos k t d
|
g |
|
|
k |
|
|
G |
cos |
d . |
||
|
|
|
|||
|
x |
|
g |
|
|
|
|
|
|||
(5.34)
Особенностью формулы (5.34) является возможность применения стандартной процедуры обратного быстрого преобразования Фурье при расчете ck .
Пример 5.5. Определить весовые коэффициенты для формирования случайного процесса с корреляционной
функцией R exp 2 2 |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Решение. Согласно (5.2) спектральная плотность |
||||||||||||||||||||||||||||||
моделируемого процесса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
G |
|
|
|
exp 2 |
|
2 2 . |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
Подставляя |
|
это |
выражение |
в |
|
(5.34) |
и |
|
|
учитывая, |
что |
||||||||||||||||||||
t 1, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 g |
|
|
2 |
|
|
|
|
|
k |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 2 |
|
|||||||||||||||
ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
exp k |
|
. |
||||||
|
|
|
|
|
|
|
exp |
|
|
|
2 |
|
|
cos |
|
|
|
|
|
|
|
|
|
||||||||
|
g |
0 |
|
|
|
|
|
4 |
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.35) |
||||
Выражение |
(5.35) |
совпадает |
с |
приведенным |
в табл. |
5.1 |
|||||||||||||||||||||||||
98

значением ck , полученным другим методом.
Данный метод расчета коэффициентов ck обеспечивает совпадение спектральных характеристик непрерывного x t и
дискретного x j процессов, но их корреляционные функции в
общем случае могут не совпадать. Однако это отличие незначительно при t 0.
Метод, основанный на разложении корреляционной функции процесса. Обозначая n j m, перепишем выражение для дискретной корреляционной функции процесса x j (5.20)
в виде
L n
R n ckck m .
k 0
Изменяя n от 0 до L, получаем систему уравнений относительно ck :
R 0 c2 c2 c2, |
|
||
0 |
1 |
L |
|
R1 c0c1 |
c1c2 |
cL 1cL |
, ... |
R n c0cn |
|
|
(5.36) |
c1cn 1 cL ncL,... |
|||
R L c0cL.
Система уравнений (5.36) может быть решена численными методами. Однако на практике эта задача является весьма сложной, так как должна быть локализована многомерная область в пространстве переменных c0, ,cL ,
содержащая нужное решение, должно быть задано начальное приближение для расчета данных коэффициентов, и определитель матрицы Якоби для системы (5.36) не должен обращаться в нуль. В этой связи для решения (5.36), как правило, применяют рекуррентный алгоритм оценивания:
c00 
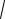 R 0 ,
R 0 ,
99
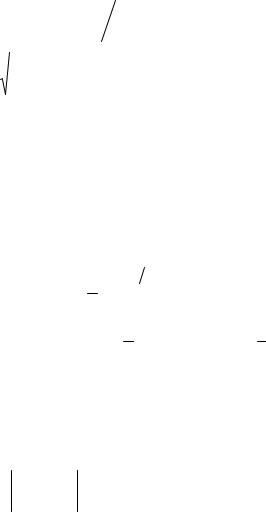
|
|
|
|
|
0, |
|
|
|
|
|
|
если k l, |
|
l |
|
|
|
|
L k |
|
l |
|
l k |
|
|||
ck |
|
|
l k |
, если k l, |
|||||||||
|
|
|
|
|
|
R k ci |
|
ci k |
|
c0 |
|||
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c0l |
|
L |
|
|
|
|
|
|
|
|
|
|
|
R 0 cil 2 , |
|
|
||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
где l 0,1,2, – номер итерации. |
|
|
|
|
|||||||||
Пример |
5.6. |
Пусть |
задана |
корреляционная функция |
|||||||||
R 1 |
|
|
|
. |
Для наглядности, чтобы число коэффициентов |
||||||||
|
|
||||||||||||
скользящего суммирования было не слишком большим, выберем шаг дискретизации равным t 0,5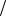 (в
(в
практических расчетах следует выбирать t 0,01 0,05 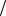 ).
).
Тогда (5.36) запишется в виде:
c2 |
c2 |
1, |
c c 1 2. |
|
0 |
1 |
|
0 |
1 |
Нетрудно видеть, что c0 c1 
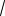 2 . Отсюда следует множество возможных решений. Для целей моделирования могут быть выбраны следующие два: а) c0 c1
2 . Отсюда следует множество возможных решений. Для целей моделирования могут быть выбраны следующие два: а) c0 c1 
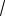 2
2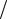 2, б) c0 c1
2, б) c0 c1 
 2
2 2.
2.
Поскольку на практике невозможно реализовать операцию суммирования бесконечно большого числа слагаемых, количество весовых коэффициентов в (5.25) необходимо ограничить. Используя (5.26), это можно сделать, исходя из условия
L |
|
1 ck2 |
1 1. |
kL
Впрактических приложениях 1 берут равным 10 3 10 4 . Это соответствует ограничению коэффициентов ck по уровню
10 2 10 3 .
Пример 5.7. При формировании случайного процесса с корреляционной функцией R exp 
 коэффициенты ck
коэффициенты ck
100
