3. Механизмы Чебышева

Из направляющих механизмов наиболее широко распространены механизмы, воспроизводящие дуги окружностей (круговые направляющие механизмы) и отрезки прямых линий (прямолинейно направляющие механизмы). Задачи синтеза таких механизмов впервые были исследованы П.Л. Чебышевым методами теории приближения функций в предположении, что воспроизводимые ими кривые имеют хотя бы одну ось симметрии.

Один из механизмов Чебышева (рисунок 5.7) предназначен для преобразования непрерывного равномерного движения кривошипа АВ в качательное движение звена ЕF с длительной остановкой (выстоем) в крайнем положении.

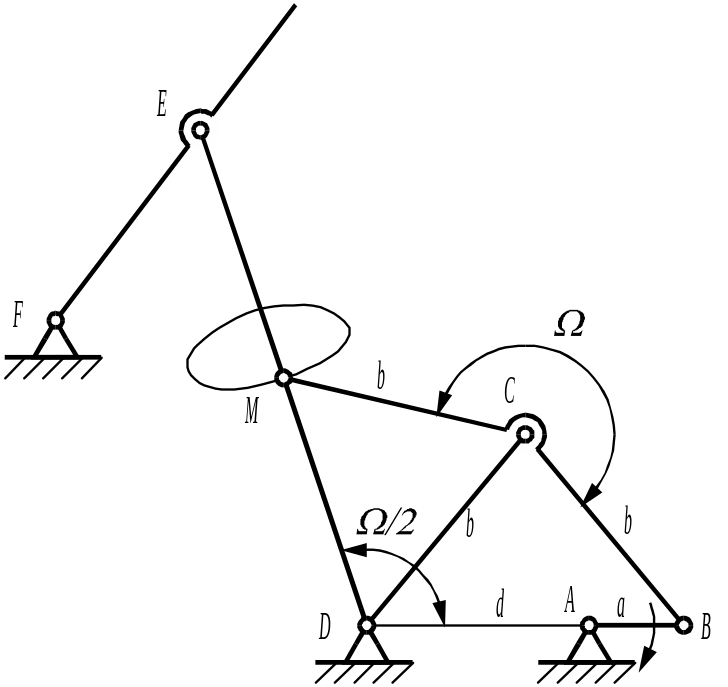
Рисунок 5.94

Для механизма характерно условие

BС = CD=CM=b, (5.3)

в силу которого траектория точки М симметрична относительно оси, проходящей через точку D под углом к стойке АD, где  – угол между частями ВС и МС шатуна. Величины a, d,  выбираются из условий наилучшего приближения шатунной кривой дуге окружности с центром на оси симметрии. При выполнении этих условий шатунная кривая пересекает окружность шесть раз, достигая семь раз предельного отклонения при чередовании его знака.

Пусть длина звена ЕМ равна радиусу окружности, к которой наиболее близка шатунная кривая, и пусть точка Е в крайнем положении попадает в центр этой окружности. Тогда при движении точки М по части кривой, близкой к окружности точки Е, звено EF будет почти неподвижным, а при движении по остальной части – звено ЕF будет перемещаться на заданный угол размаха, определяемый параметрами механизма. Таким образом реализуется длительный выстой звена.

Если в рассмотренном механизме сохранить условие (5.2), сделать  равным  и отбросить звенья EF и ЕМ, то получится прямолинейный направляющий механизм Чебышева (рисунок 5.8). Этот механизм получается из рассмотренного выше механизма Чебышева увеличением длины звена ЕМ до бесконечности и поэтому является частным случаем этого механизма.

Основные параметры этого механизма а, b и d должны удовлетворять условию 3d – а = b, при котором траектория точки М наименее отклоняется от прямой линии и выполняются условия наилучшего приближения. При этом условии шатунная кривая имеет шесть точек пересечения с прямой, а предельное отклонение достигается семь раз при последовательно меняющихся знаках. О точности воспроизведения прямой можно судить по следующим результатам: при d = 2,22, a отношение максимального отклонения от прямой линии к длине прямолинейного участка не превосходит 10^-3. Такое отклонение графическими методами не обнаруживается. За сходство рассмотренного прямолинейного направляющего механизма Чебышева в среднем положении (рисунок 5.8) с буквой  он называется иногда лямбдообразный.

На рисунке 5.8 штриховыми линиями показан шарнирный четырехзвенник А₁B₁C₁D₁, являющийся модификацией лямбдообразного механизма и называемый перекрестным. При

А₁B₁=C₁D₁=2b,

B₁M=a,

B₁C₁=2a,

А₁D₁=2d

перекрестный и лямбдообразный механизмы описывают точкой М одинаковые траектории.

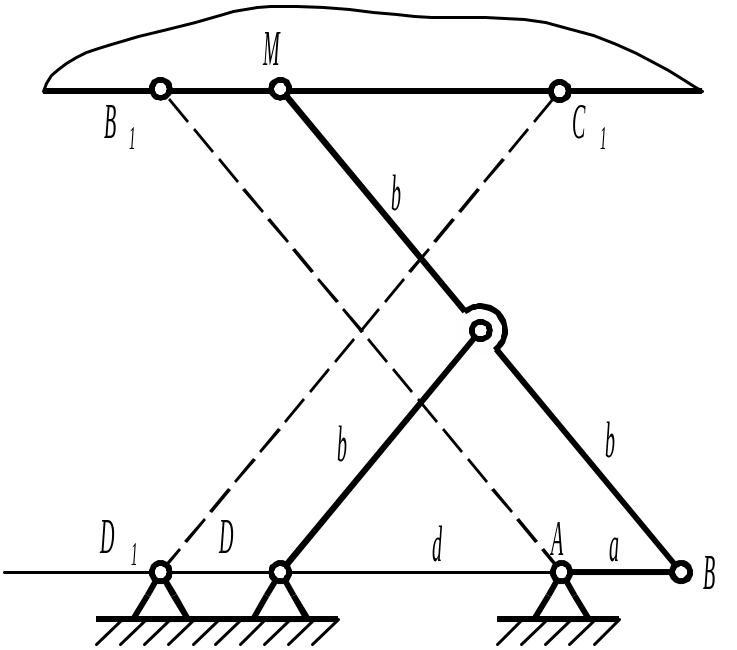
Рисунок 5.95

4. Теорема Робертса

При синтезе приближенных направляющих механизмов необходимо учитывать дополнительные условия синтеза: ограничения на угол давления, на скорости и ускорения точек некоторых звеньев, а также другие условия. Поэтому очень важной и широко используемой при синтезе приближенных направляющих механизмов является теорема Робертса: любая шатунная кривая шарнирного четырехзвенника может быть воспроизведена в общем случае тремя различными шарнирными четырехзвенниками.

Эта теорема допускает преобразования шарнирных четырехзвенииков при сохранении их способности к воспроизведению заданной кривой. Значение этих преобразований для практики велико потому, что, имея один из механизмов, воспроизводящих заданную кривую, можно создать два других механизма, воспроизводящих ту же кривую, и из них выбрать лучший по дополнительным условиям синтеза.

Пусть имеется четырехзвенник А₁B₁C₁D₁, воспроизводящий точкой М шатуна некоторую кривую (рисунок 5.9).

Два других четырехзвенника, воспроизводящих ту же кривую, строятся в следующем порядке:

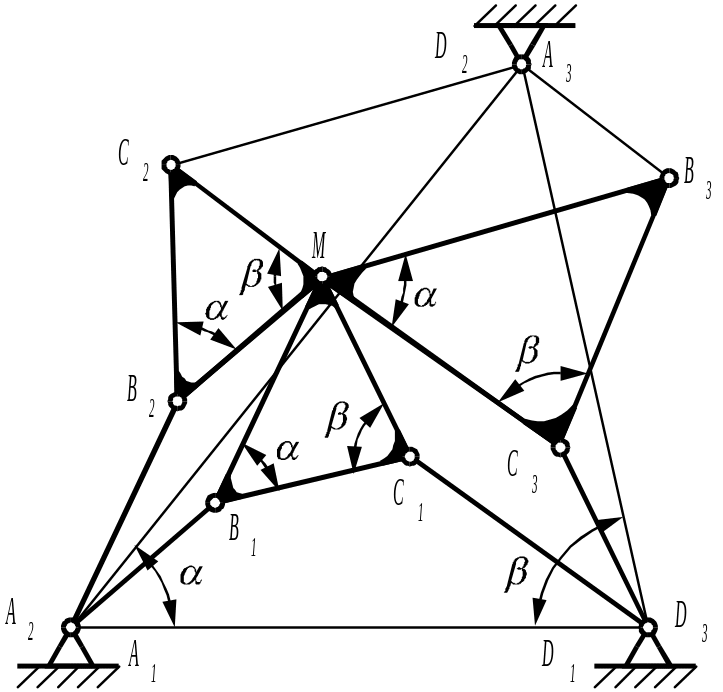
Рисунок 5.96

На отрезке А₁D₁ строится треугольник, подобный треугольнику B₁C₁М. В вершине этого треугольника размещаются оси кинематических пар D₂ и А₃ искомых четырехзвенников, ось пары А₂ совпадает с осью пары А₁, а ось пары D₃ совпадает с осью пары D₁.

На сторонах МС₁ и С₁D₁=C₁D₃ строится параллелограмм МС₁D₃C₃, а на сторонах MB₁ и А₁B₁=А₁B₂ – параллелограмм МB₁A₂B₂. На отрезках МВ₂ и МС₃ строятся треугольники МВ₂С₂ и МВ₃С₃, подобные треугольнику МС₁В₁, у которых стороны MB₂ и МС₃ подобны стороне В₁С₁.

Соединение точек С₂ и В₃ с точками D₂ и A₃, совпадающими друг с другом и построенными ранее, дает кинематические схемы искомых направляющих четырехзвенников. Фигура МС₂D₂B₃ должна мало отличаться от параллелограмма. В противном случае построения неверны.

В частном случае, когда точка М лежит на одной прямой, соединяющей центры шарниров В и С шатуна (рисунок 5.9), точка С₂ лежит на линии А₁С₁, а точка В₃ – на линии B₁D₁. В этом случае построение подобных треугольников заменяется построением подобных отрезков.

Теорема Робертса применима и к другим типам плоских механизмов, но построения механизмов, равноценных по способности воспроизводить заданную кривую, отличаются от рассмотренных выше построений.