5. Силы инерции звена, совершающего плоское движение

В механизме на рисунке 4.14 также можно найти такой центр приведения, для которого M_u=0, т.е. система сил инерции может быть сведена к равнодействующей. Как видим, только в случае поступательного движения линия действия равнодействующей сил инерции проходит через центр тяжести звена.

(4.17)

(4.18)

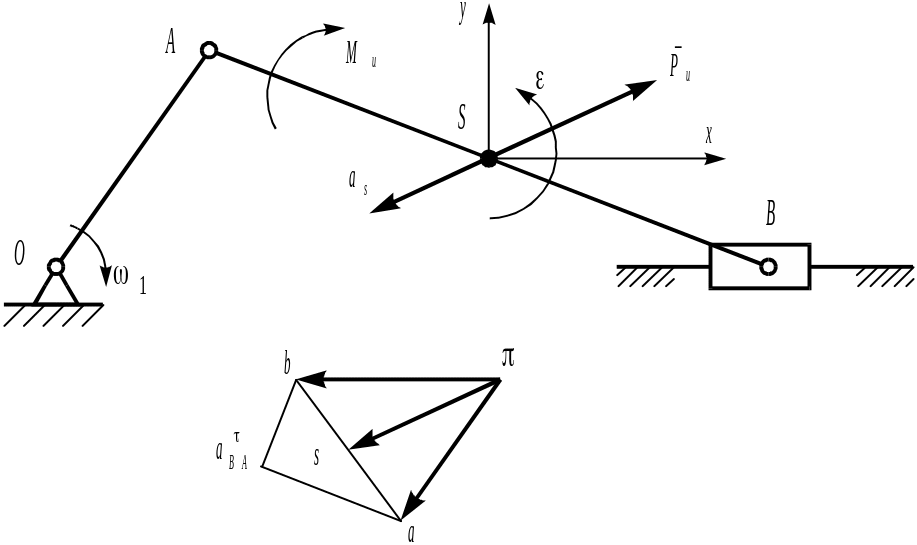
Рисунок 4.63

3. Определение реакций в кинематических парах групп Ассура

С целью проведения силового расчета механизм расчленяется на группы Ассура. Расчет начинается с той группы, в состав которой входит выходное звено. Затем последовательно рассчитываются все группы, и заканчивается силовой анализ расчетом входного звена механизма. Методика расчета всех групп II класса едина.

Определение реакций в кинематических парах групп с помощью метода кинетостатики рекомендуется проводить в следующем порядке.

1. Изобразить группу Ассура в заданном положении, вычертив ее в соответствующем масштабе.

2. Приложить к звеньям группы все заданные силы и неизвестные реакции в кинематических парах.

3. Приложить к звеньям группы силы инерции и моменты сил инерции.

4. Согласно принципу отвердевания и принципу Даламбера составить уравнение равновесия для группы в целом, как для твердого тела. Записывая уравнение равновесия для группы, следует придерживаться определенного порядка: вначале записать все силы, действующие на одно звено, затем записать все силы, действующие на другое звено. Запись уравнения следует начинать и заканчивать неизвестными реакциями. Для большей ясности в уравнение следует включать и внутренние реакции (рисунок 4.15, б). Сложение векторов сил проводится в той же последовательности, в которой велась запись уравнения.

Проследим этот порядок на примере группы с тремя вращательными парами, входящей в состав шарнирного четырехзвенника. Составим уравнение равновесия группы:

;

По этому уравнению построить план сил не удастся, т.к. если построение плана свести к построению треугольника, представив все известные силы как одну сторону треугольника, то увидим, что две другие стороны включают силы, величины и направления которых не известны. Такой треугольник построить невозможно. В этом случае надо использовать уравнение равновесия моментов сил, разложив одну из реакций на два направления, пустив одну из составляющих реакции через ту точку, относительно которой будет составляться уравнение моментов. Составим уравнение моментов относительно точки B для звена 2. Выбирая точку В в качестве центра, мы исключаем тем самым из уравнения моментов нормальную составляющую реакций R₁₂ в шарнире А и реакцию R₃₂ в шарнире В. Итак,

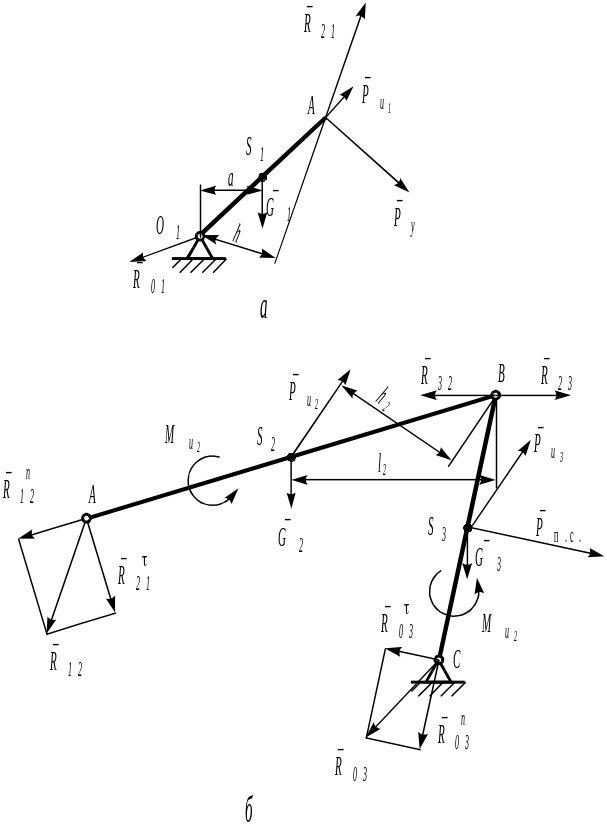
Рисунок 4.64

.

Разрешая это уравнение относительно , получим ее величину. Направление реакции определяется ее знаком. После определения этой составляющей видим, что план сил и в этом случае построить не удается. Тогда таким же образом поступаем с реакцией R₃₀, раскладывая ее на две составляющие и составляя уравнение моментов относительно точки В для звена 3, находим .

Рассматривая уравнение равновесия после того, как силы отправлены в категорию известных сил, видим, что треугольник, у которого одна сторона известна по величине и направлению, а две другие ( ) известны по направлению, построить можно. Поэтому приступаем к построению плана сил (рисунок 4.16).

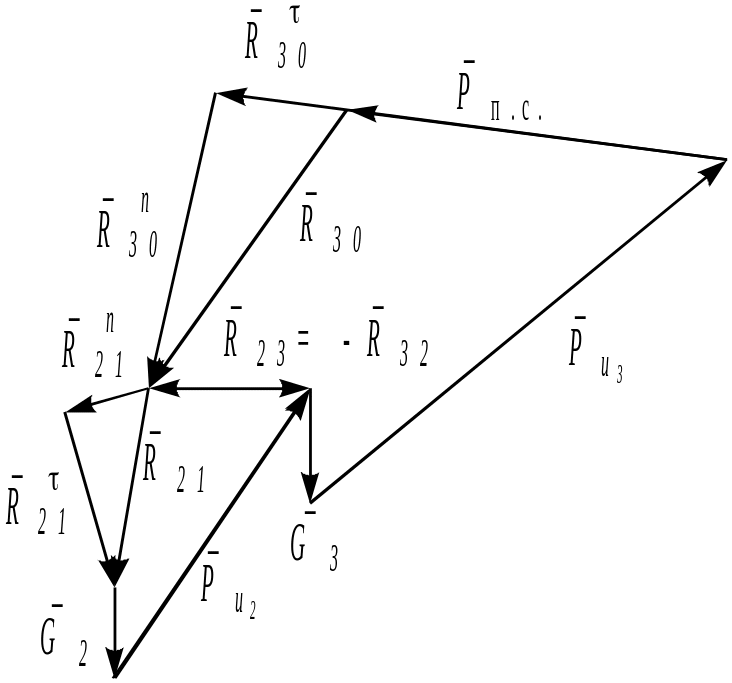
Рисунок 4.65

Далее определяем реакции во внутренней паре. Для этого составляем уравнение равновесия для какого-либо одного звена (составление уравнения заключается в простом переписывании части уже составленного уравнения для группы). Напишем уравнение для звена 2, освобождая его от связей в точке В:

R₂₁ +G₂+P_u2+ R₂₃  = 0.

Для определения R₃₂ используем уже построенный для группы план сил:

R₃₂ = – R₂₃ .