9. Структурные группы пространственных механизмов

Принцип образования механизмов является общим для плоских и пространственных. Условие существования пространственных структурных групп то же, т.е. W=0.

Степень свободы определяется выражением

W = 6n – 5Р₅ – 4Р₄ – 3Р₃ – 2Р₂ – Р₁.

Пусть пространственный механизм состоит из звеньев, соединенных парами только 5-го класса (рисунок 3.25). Структурная формула для него имеет вид W=6n-5Р₅. Условие существования групп: W_гр. = 0, т.е. 6n=5Р₅. Структурная группа будет выглядеть так: n = 5; 5Р₅=6n; W=0.

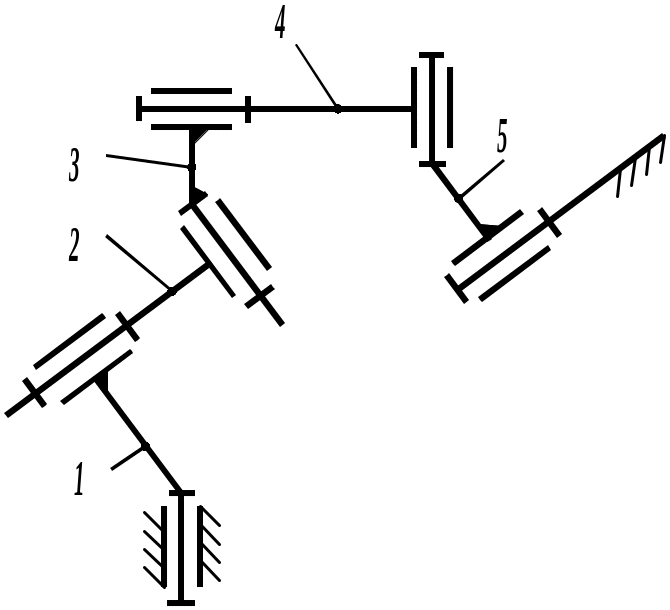
Рисунок 3.47

Структурная группа получается громоздкой. Выберем другой состав звеньев и пар в механизме (рисунок 3.26).

W = 6n – 5Р₅ – 4Р₄ – 3Р₃

Рисунок 3.48

Условие существования группы: W_гр. = 0, т.е.

6n = 5Р₅ + 4Р₄ + 3Р₃.

В этом случае n=2; Р₅=1; Р₄=1; Р₃=1.

Если такую группу присоединим к начальному звену, движение которого определяет одна обобщенная координата, получим пространственный механизм со степенью свободы равной единице (рисунок 3.27)

n=3; Р₅=2; Р₄=1; Р₃=1; W = 6  3 – 5  2 – 4  1 – 3  1 – 1.

Рисунок 3.49

Следовательно, принцип образования пространственных механизмов сохраняется.

4. Анализ механизмов

   1. Кинематический анализ механизмов

Кинематический анализ механизмов – это изучение движения звеньев механизма без учета сил, вызывающих движение. Определяющим фактором здесь является степень свободы механизма. Закон движения ведущих (начальных) звеньев известен, поэтому можно сказать, что кинематический анализ состоит в определении движения звеньев механизма по заданному движению начальных звеньев.

Основные задачи кинематического анализа следующие:

1) определение положений звеньев, включая определение траекторий движения отдельных точек;

2) определение передаточных функций, скоростей и ускорений звеньев механизма.

Методы кинематического анализа:

1) аналитические;

2) графоаналитические;

3) графические;

4) экспериментальные.

В настоящее время аналитические методы анализа выходят на первое место, чему способствует развитие ЭВМ. Однако графоаналитические и графические методы хотя и уступают в точности получаемых результатов, широко распространены из-за своей наглядности и доступности.

Ниже рассмотрено аналитическое решение задачи о положениях звеньев механизма по методу преобразования координат. Метод предложен Ю.Ф. Морошкиным.

1. Графическое определение положений звеньев механизма и построение траектории

Для решения поставленной задачи должны быть заданы кинематическая схема механизма и закон движения ведущего (начального) звена.

Для определения положений звеньев механизма кинематическая схема выполняется в масштабе. Для этого выбирается масштабный коэффициент _ (м/мм), который показывает, сколько метров натуры содержится в одном мм чертежа.

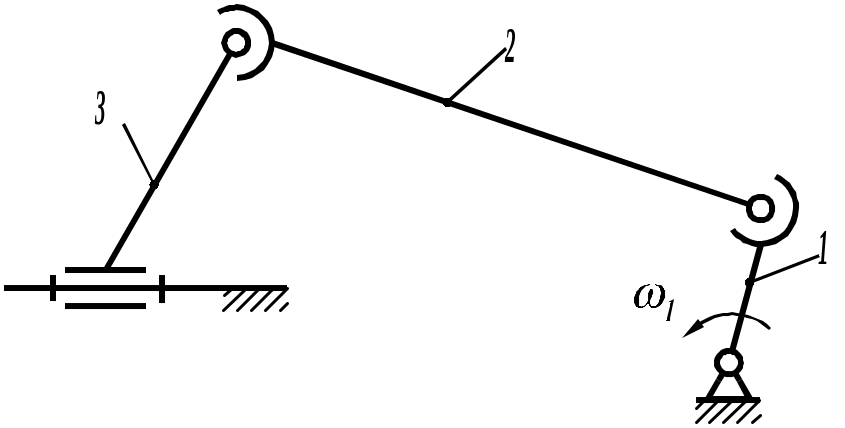
Пусть задана схема механизма 2-го класса (рисунок 4.1). Известны размеры звеньев механизма _AB, _BC, _CD, _AD и закон движения ведущего звена. Механизм имеет ведущее звено АВ.

Рисунок 4.50

Построение начинается с определения положения неподвижных точек механизма А и D (_AD). Затем описываем окружность радиусом _AB и вторую – радиусом _CD (рисунок 4.2).

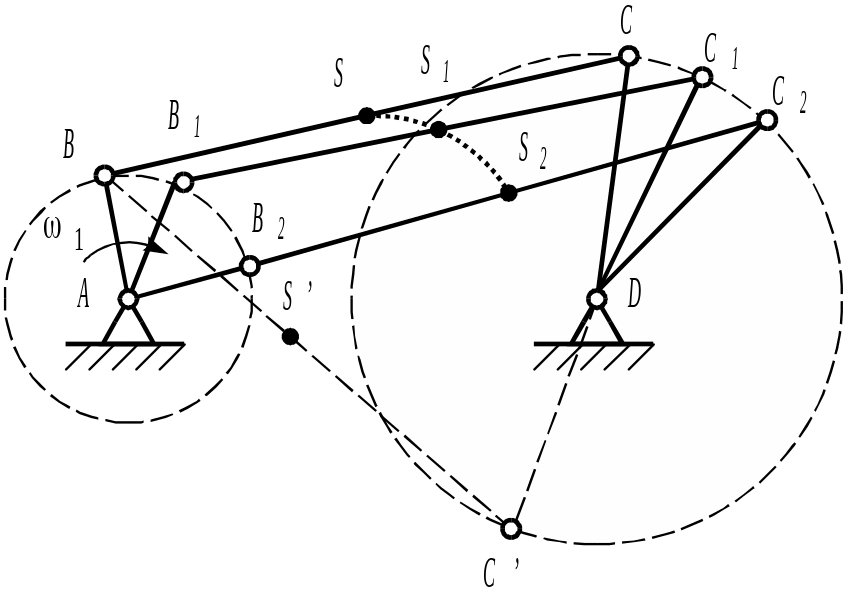
Рисунок 4.51

Выбрав положение звена АВ, определяемое значением обобщенной координаты ₁, находим методом засечек положение остальных звеньев ВС и СD.

Точно также можно найти ряд других положений механизма. Будем считать ₁=const, тогда откладывая равные углы от положения кривошипа АВ, найдем положение механизма АВ₁С₁D и т.д. Затем строим траекторию точки S, лежащей на звене ВС.

При построении положений звеньев механизма при одном положении звена АВ звенья ВС и СD могут занимать два положения ВС и СD или ВС и C D. Это разные механизмы, здесь проявляет себя свойство – условие сборки.

В нашем случае допустим только первый вариант ВСD, т.к. при этом сохраняется требуемое направление угловой скорости звена СD – по часовой стрелке.

Второй вариант – В₁С₁D – это уже другой механизм, т.к. СD вращается против часовой стрелки.